文章信息
- 赵天贺, 汪伟, 寇博晨, 沈晨晖, 孙中兴
- ZHAO Tianhe, WANG Wei, KOU Bochen, SHEN Chenhui, SUN Zhongxing
- 平面传感器阵列测试振动角速度算法研究
- Research on measurement of vibration angular velocity of planar sensor array
- 中国测试, 2018, 44(6): 105-108
- CHINA MEASUREMENT & TEST, 2018, 44(6): 105-108
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018.06.020
-
文章历史
- 收稿日期: 2017-12-25
- 收到修改稿日期: 2018-01-11
现代武器装备发展迅速,为了提升飞机、坦克、火炮等的使用性能,使其在复杂战场环境下能够更好地完成任务,需要对其产生的运动参数进行监控[1]。这类运动体运动自由度大、动态范围广,振动状态为较高频率下多维线振动和角振动的耦合[2]。单维的传感器测试技术、陀螺仪技术、CCD成像技术等传统振动测试手段很难在该测试环境中得到应用[3]。加速度传感器阵列可以有效地对该类振动进行监测,解决了工程中对上述运动体进行六自由度参数测试的难题[4]。
近年来,国内外加速度传感器阵列的配置方案越来越多,典型的传感器配置方案有六加速度、九加速度、十二加速度阵列构型[5-6]。在工程实现过程中,发现空间配置方案会增大测量设备的体积,本文通过对构型设计的深入研究,设计了一种基于平面的加速度传感器配置方案,解决了测量设备的体积问题。
采用加速度传感器阵列测量六自由度参数,角速度的解算非常关键,其准确度直接影响着最终测量结果的准确性。目前,传统的角速度解算方法有积分法、开方法等。在新的构型当中单一的积分法会随着时间的积累产生严重的发散型误差,单一的开方算法得不到含有符号的解算值,组合的开方法会产生严重的小角度误判现象。本文在对算法进行原理推理和仿真分析的基础上,通过比较其优缺点及分析加速度传感器输出方程,设计了多种角速度融合的组合方法[7],可以使角速度的误差满足允许范围,具有较大的实用价值。
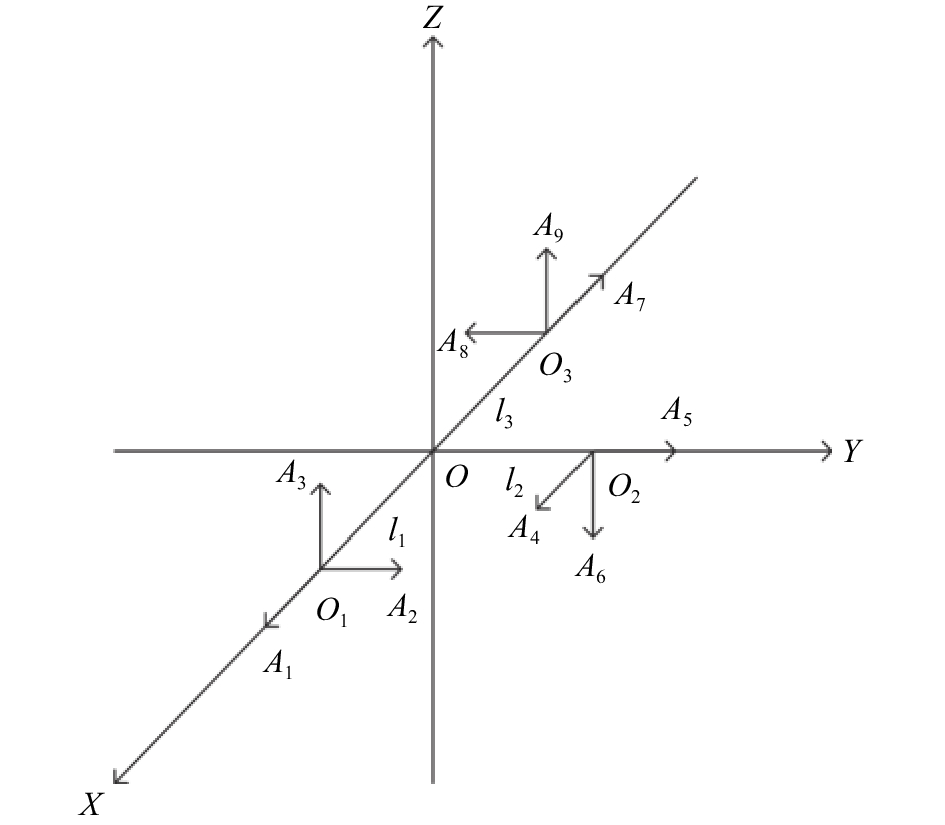
1 传感器阵列测试方案安装配置方式如图1所示,O-XYZ为建立的载体坐标系,在O-XY平面内安装3个三轴加速度传感器时,分别使传感器的一个敏感轴重合安装于X轴或Y轴坐标轴,另外两轴垂直于该坐标系。其中
|
| 图 1 平面加速度计阵列安装示意图 |
9个传感器相对于载体坐标系原点的位置坐标矩阵r和敏感方向坐标矩阵θ为
| $\begin{array}{l}{ r} = \left[ {\begin{array}{*{20}{l}}{{l_1}} & {{l_1}} & {{l_1}} & 0 & 0 & 0 & { - {l_3}} & { - {l_3}} & { - {l_3}}0 & 0 & 0 & {{l_2}} & {{l_2}} & {{l_2}} & 0 & 0 & 00 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}} \right]{ \theta } = \left[ {\begin{array}{*{20}{l}}1 & 0 & 0 & 1 & 0 & 0 & \!\!{ - 1} & 0 & 00 & 1 & 0 & 0 & 1 & 0 & 0 & \,{ - 1} & 00 & 0 & 1 & 0 & 0 & { - 1} & 0 & 0 & 1\end{array}} \right]\end{array}$ | (1) |
根据运动学方程可以得到基于线加速度计捷联惯导系统上任意加速度计的输出[8-10]为
| ${ f} = { J}\left[ {\begin{array}{*{20}{c}}{\dot { \omega} }{}\\{ A}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{{ \theta _1}^{\rm T}{ \Omega ^2}{{ r}_1}}\\ \vdots \;{{ \theta\!_N}^{\rm T}\!{ \Omega ^2}{{ r}_N}}\end{array}} \right]$ | (2) |
式中:
A——载体坐标系3个坐标轴方向上的线加速度。
其中:
| $\quad\;\;\;\;\;\begin{array}{l}\dot { \omega} = {\left[ {\begin{array}{*{20}{c}}{{{\dot \omega }_x}}\\{{{\dot \omega }_y}}\\{{{\dot \omega }_z}}\end{array}} \right]^{\rm T}}\;\;{ A} = {\left[ {\begin{array}{*{20}{c}}{{A_x}}\\{{A_y}}\\{{A_z}}\end{array}} \right]^{\rm T}}{ \Omega ^2} = \left[ {\begin{array}{*{20}{c}}{ - \omega _y^2 - \omega _z^2} & {{\omega _x}{\omega _y}} & {{\omega _x}{\omega _z}}\\{{\omega _x}{\omega _y}} & { - \omega _x^2 - \omega _z^2} & {{\omega _x}{\omega _y}}\\{{\omega _x}{\omega _z}} & {{\omega _y}{\omega _z}} & { - \omega _x^2 - \omega _y^2}\end{array}} \right]{ J} = \left[ {{{\begin{array}{*{20}{c}}{{{ J}_1}^{\rm T}} & {{{ J}_2}}^{\rm T}\end{array}}}} \right]{{ J}_2} = \theta { r} = \left[\!\!\!\!\!\!\!\!\!\!\!{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{r_1}} & {{r_2}} & {{r_3}} & {{r_4}}\end{array}} & {{r_5}} & {{r_6}}\end{array}} & {{r_7}} & {\begin{array}{*{20}{c}}{{r_8}} & {{r_9}}\end{array}}\end{array}} \!\!\!\!\!\!\!\!\!\right]{ \theta} = \left[\!\!\!\!\!\!\!\!\!\!\! {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{\theta _1}} & {{\theta _2}} & {{\theta _3}} & {{\theta _4}}\end{array}} & {{\theta _5}} & {{\theta _6}}\end{array}} & {{\theta _7}} & {\begin{array}{*{20}{c}}{{\theta _8}} & {{\theta _9}}\end{array}}\end{array}} \!\!\!\!\!\!\!\!\!\right]{{ J}_1} = \left[ {\begin{array}{*{20}{c}}{{r_1} \times {\theta _1}} & {{r_2} \times {\theta _2}} & \cdots & {{r_9} \times {\theta _9}}\end{array}} \right]\end{array}$ | (3) |
将式(2)完全展开可以得到关于载体坐标系的角速度、角加速度和线加速度等变量,与9个加速度传感器在其敏感方向上加速度信号的方程组为
| $\left\{ \begin{array}{l}{f_1} = {A_x} - {l_1}({\omega _y}^2 + {\omega _z}^2)\\{f_2} = {A_y} + {l_1}({{\dot \omega }_z} + {\omega _x}{\omega _y}){f_3} = {A_z} - {l_1}({{\dot \omega }_y} - {\omega _x}{\omega _z}){f_4} = {A_x} + {l_2}({\omega _x}{\omega _y} - {{\dot \omega }_z}){f_5} = {A_y} - {l_2}({\omega _x}^2 + {\omega _z}^2)\\{f_6} = - {A_z} - {l_2}({{\dot \omega }_x} + {\omega _y}{\omega _z}){f_7} = - {A_x} - {l_3}({\omega _y}^2 + {\omega _z}^2)\\{f_8} = - {A_y} + {l_3}({{\dot \omega }_z} + {\omega _x}{\omega _y}){f_9} = {A_z} - {l_3}({{\dot \omega }_y} - {\omega _x}{\omega _z})\end{array}\right.$ | (4) |
根据式(4)可以解算得到表征六自由度的相关参数的相互关系表达式为
| $\left\{\begin{array}{l}{A_x} = \displaystyle\frac{{{l_3}{f_1} - {l_1}{f_3}}}{{{l_1} + {l_3}}}\\ {A_y} = \displaystyle\frac{{{l_3}{f_2} - {l_1}{f_8}}}{{{l_1} + {l_3}}}\\ {A_z} = \displaystyle\frac{{{l_3}{f_3} - {l_1}{f_9}}}{{{l_1} + {l_3}}}\\ [{\omega _y}^2 + {\omega _z}^2 = - \displaystyle\frac{{{f_1} + {f_7}}}{{{l_1} + {l_3}}}\\ {\omega _y}^2 - {\omega _x}^2 = \displaystyle\frac{{{l_3}({f_2} - {f_5}) - {l_1}({f_5} + {f_8}) + {l_2}({f_1} + {f_7})}}{{{l_2}({l_1} + {l_3})}}\\ {\omega _x}^2 + {\omega _z}^2 = \displaystyle\frac{{{l_3}({f_2} - {f_5}) - {l_1}({f_5} + {f_8})}}{{{l_2}({l_1} + {l_3})}}\\ {{\dot \omega }_z} = \displaystyle\frac{{{l_3}({f_1} - {f_4}) - {l_1}({f_4} - {f_7})}}{{2{l_2}({l_1} + {l_3})}} - \frac{{{f_2} + {f_8}}}{{{l_1} + {l_3}}}{\omega _x}{\omega _y} = \displaystyle\frac{{{l_3}({f_1} - {f_4}) - {l_1}({f_4} - {f_7})}}{{2{l_2}({l_1} + {l_3})}} + \displaystyle\frac{{{l_3}{f_9} - {l_1}{f_8}}}{{{l_2}({l_1} + {l_3})}}\end{array}\right.$ | (5) |
应用式(5)解算得到的角速度平方项、Z轴的角加速度以及角速度的乘积项,可以应用积分法、开方法和组合算法求解3个坐标轴的角速度。
2.1 积分法在载体坐标系初始时刻角速度值已知的情况下,根据式(5)通过直接积分解算3个坐标系的角速度。设置坐标系角速度初始值为
| $\left\{ {\begin{array}{*{20}{c}}{{\omega _x}(t) = {\omega _x}(t - 1) + {{\dot \omega }_x}(t)\Delta t}{{\omega _y}(t) = {\omega _y}(t - 1) + {{\dot \omega }_y}(t)\Delta t}{{\omega _z}(t) = {\omega _z}(t - 1) + {{\dot \omega }_z}(t)\Delta t}{t = 1,2, \cdots ,n}\end{array}} \right.$ | (6) |
将解算的
根据式(5)中的平方项可以求得
| $\left\{ {\begin{array}{*{20}{c}}{{\omega _x}(t) = {\rm sign}({\omega _x}(t)) \times \left| {{\omega _x}(t)} \right|}{{\omega _y}(t) = {\rm sign}({\omega _y}(t)) \times \left| {{\omega _y}(t)} \right|}{{\omega _z}(t) = {\rm sign}({\omega _z}(t)) \times \left| {{\omega _z}(t)} \right|}{t = 1,2, \cdots ,n}\end{array}} \right.$ | (7) |
应用开方法进行角速度的解算过程中,解算数值不随时间积累,避免了较大误差的产生,但其应用的是积分法解算值的符号,仍然存在符号误判的现象,随着时间的积累,符号误判对结果的影响持续增大。
2.3 组合算法通过对多种解算方法的分析与比较,针对平面加速度阵列构型设计了一种积分法、开方法相结合的组合算法进行角速度的解算[12],应用开方法中获得的
为了验证针对平面构型设计的角速度解算算法的可行性,搭建模型对其进行比较和分析。在仿真中取采样频率为1 kHz,采样时间为1 000 s,加速度传感器常值误差为0.000 1 g,随机噪声的均方差为0.001 g。
角速度参数设置为
| $\left\{ \begin{array}{l}{\omega _x} = 5\sin (100t)\\{\omega _y} = 5\cos (80t)\\{\omega _z} = 5\sin (60t)\end{array} \right.$ | (8) |
线加速度参数设置为
| $\left\{ \begin{array}{l}{A_x}{\rm{ = 600cos(60}}t{\rm{)}}\\{A_y}{\rm{ = 800cos(80}}t{\rm{)}}\\{A_z}{\rm{ = 1\,000cos(100}}t{\rm{)}}\end{array} \right.$ | (9) |
对3种算法进行仿真,并分别对其X轴、Y轴角速度误差进行分析,如图2~图4所示。
|
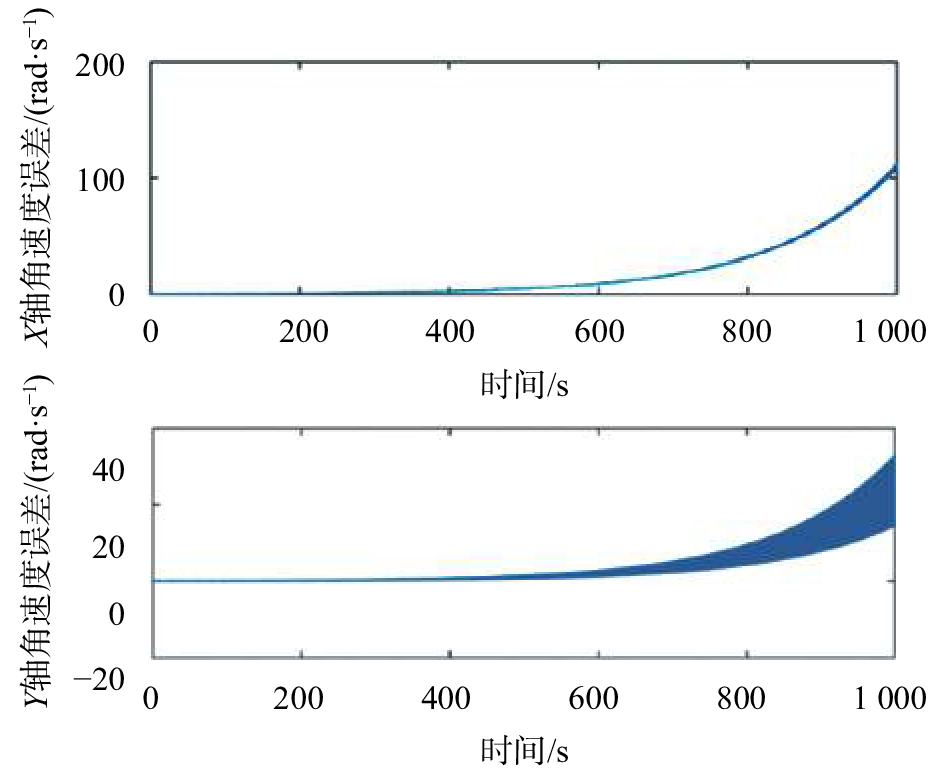
| 图 3 开方法角速度误差 |
|
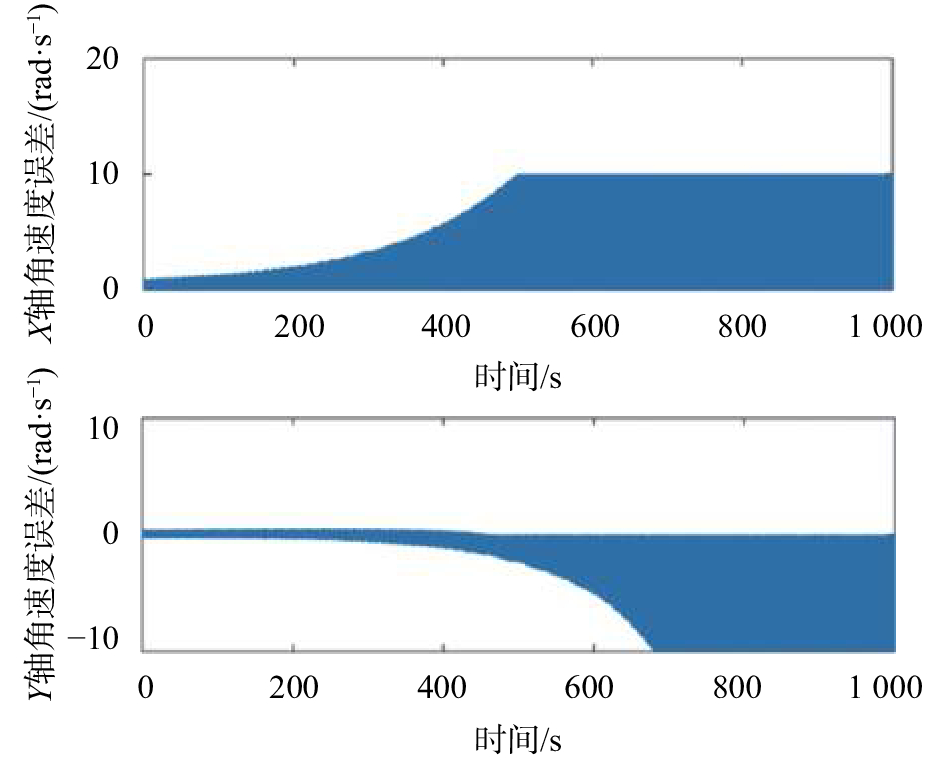
| 图 4 组合算法角速度误差 |
从图2可以看出,积分法解算的角速度误差随时间不断积累发散。当测试时间较短时,误差较小,但一旦时间增长,其误差呈指数形式增长。由此可见,该算法不可应用于平面加速度传感器阵列的姿态解算当中。
从图3开方法仿真曲线可以看出,角速度误差在随着时间积累到10 rad/s后将不再增长。仿真说明开方法虽然解决了单一的积分法的误差积累问题,但开方法中的积分获取符号成分对其造成的符号误判现象随着时间的延长不断严重,难以获得较真实的角速度解算值。因此结合积分法的开方法也很难应用到新的构型当中。

|
| 图 2 积分法角速度误差 |
从图4组合算法仿真可以看出,组合算法解算的角速度误差稳定在
为实现传感器阵列技术在运动体复杂振动测试领域的工程应用,设计实际符合要求的传感器配置方案。该文介绍一种平面传感器阵列,角速度解算作为传感器阵列振动测试的关键环节。针对新的构型,通过学习传统解算手段设计3种解算方法,其中积分法误差随时间积累严重,开方法符号误判不可避免。组合算法有效地避免积分算法的误差积累和小、角速度的符号误判问题,在长时间的仿真计算过程中仍然能保持较高准确度,对传感器阵列振动测试技术的工程实现具有一定的意义。
| [1] |
赵天贺, 汪伟. 基于MEMS技术的捷联惯导系统现状[J].
飞航导弹, 2017(10): 17-21.
|
| [2] |
汪伟, 焦健超, 唐力伟, 等. 基于传感器阵列的振动测试角速度算法研究[J].
中国测试, 2012, 38(4): 58-61.
|
| [3] |
焦健超. 火控系统观瞄器件复杂振动环境参数测试技术研究[D]. 石家庄: 陆军工程大学石家庄校区, 2011.
|
| [4] |
焦健超, 汪伟, 唐力伟, 等. 三轴加速度传感器阵列振动测试新方案[J].
中国测试, 2012, 38(3): 109-112.
|
| [5] |
杨杰. 无陀螺捷联惯导系统加速度计构型研究与误差分析[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [6] |
王东江, 杨新民. 一种无陀螺捷联惯导的九加速度计测姿方法[J].
电子测量技术, 2017, 40(10): 70-74.
DOI:10.3969/j.issn.1002-7300.2017.10.015 |
| [7] |
Qin F J, An L I, Jiang-Ning X U. Design of attitude algorithm for 13-accelerometer based inertial navigation system[J].
Journal of Chinese Inertial Technology, 2011, 19(6): 637-641.
|
| [8] |
汤传业. SINS/GPS组合测量中的捷联算法与组合滤波技术研究[D]. 南京: 东南大学, 2016.
|
| [9] |
王菲. SINS/GPS组合导航系统研究[D]. 北京: 北京理工大学, 2015.
|
| [10] |
汪伟, 歹英杰, 陈海龙, 等. 独立卡尔曼滤波器全加速度计复杂振动角速度解算[J].
中国测试, 2017, 43(5): 105-109.
DOI:10.11857/j.issn.1674-5124.2017.05.022 |
| [11] |
陈海龙. 基于加速度计阵列的装备六自由度复杂振动测试技术研究[D]. 石家庄: 军械工程学院, 2013.
|
| [12] |
李成刚, 谢志红, 尤晶晶, 夏玉辉, 魏学东. 新型无陀螺捷联惯导系统导航方案设计及建模[J].
中国惯性技术学报, 2015, 23(03): 303-310.
|
| [13] |
张慧. 捷联惯导系统自对准技术研究与仿真[D]. 太原: 中北大学, 2016.
|
 2018, Vol. 44
2018, Vol. 44