文章信息
- 张鹏, 胡昌华, 白灿, 张优, 张建勋
- ZHANG Peng, HU Changhua, BAI Can, ZHANG You, ZHANG Jianxun
- 考虑随机效应的两阶段退化系统剩余寿命预测方法
- Remaining useful life estimation method for two-phase degradation system with random effects
- 中国测试, 2019, 45(1): 1-7
- CHINA MEASUREMENT & TEST, 2019, 45(1): 1-7
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018070066
-
文章历史
- 收稿日期: 2018-07-17
- 收到修改稿日期: 2018-08-14
随着现代科学技术的飞速发展,工业设备产品呈现出集成化、智能化、复杂化的发展趋势,功能增强的同时给设备的可靠性研究带来了新的挑战。设备在运行过程中不可避免地受到外部环境和内部因素的随机影响,导致性能下降乃至退化失效,对于此类随机退化系统,采用随机过程为基础的退化建模方法进行寿命预测是很好的选择,其中基于Wiener过程的建模方法由于其良好的数学性质在退化建模和寿命预测中得到广泛应用[1]。
目前大多数基于随机过程退化建模的文献认为系统在退化过程中遵循单一的随机退化模型,而在工程实践中由于退化机理的复杂性、环境因素的影响、系统工作状态的改变等,一些设备和产品的退化速率以及数据波动程度呈现出两阶段甚至多阶段特性[2]。例如,液力耦合器的退化过程可分为两个阶段[3],第一阶段迅速退化,然后在第二阶段缓慢退化至失效,与之类似的有激光发射器[4]、等离子显示板[5-6]、有机发光二极管[7]、加速度计[8]等;也有像锂电池[9]等开始时经历一个平稳退化期,随着充放电的进行,由于固体电解质层在电极上的生长以及副反应导致的活性材料的损失,导致锂电池容量在后一阶段迅速衰落。
对于此类存在变点的两阶段随机退化系统进行退化建模和寿命预测研究,已有不少学者关注并取得一定进展。Wang等[3]提出在变点前后液力耦合器的退化分别使用伽马过程和维纳过程来控制,在此基础上详细讨论了实时可靠性评估和参数估计问题。Bae等[6]在对等离子显示板的退化研究中引入带有变点的随机系数对数线性模型,并用极大似然估计方法得到其寿命分布。Wang等[7]提出了一种以贝叶斯框架为主要内容的变点维纳过程模型,用于有机发光二极管的退化预测,与最大似然法相比分段贝叶斯方法表现出更强的鲁棒性。Chen等[10]在两阶段对数线性模型的基础上进行改进来描述滚动球轴承的分段退化过程,并用贝叶斯方法更新模型参数进行寿命预测。Yan等[11]用两阶段维纳退化过程对液力耦合器的进行可靠性评估,基于赤池信息准则和残差平方和标准估计变点。
尽管两阶段退化模型取得了一些理论与实际应用成果,但是仍然存在一些问题有待研究和解决。考虑到同批次产品之间存在差异性,其变点处的退化量以及两个阶段的退化模型参数都会存在一定的差异,目前仅有很少一部分文献[12]考虑该问题。此外,现有文献中通常假设变点处的退化量已知或其分布函数能够从历史数据统计得到,这会需要大量的历史退化数据[10]。实际上,由于第一阶段退化的不确定性,在退化过程达到变点前,变点发生处的退化量未知,并非一个确定值或期望值,是与第一阶段退化模型相关的随机变量,在进行首达时间意义下的剩余寿命预测时,必须考虑这一点。
综上本文在两阶段维纳退化模型的基础上,引入随机效应来描述样本间的差异性,研究了剩余寿命预测中的模型参数的离线辨识和在线更新算法,最后通过液力耦合器的实例研究验证了本文所提方法可以有效实现对两阶段退化设备的剩余寿命预测。
1 两阶段Wiener过程退化模型 1.1 退化模型的假设假设1 系统性能退化过程呈现两阶段特征,存在变点,变点前后两个阶段退化速率存在显著差异。
假设2 在各个阶段,系统的退化过程
| $X\left( t \right) = {x_0} + \mu t + \sigma B(t)$ | (1) |
其中
假设3 系统的寿命定义基于随机过程的首达时间概念[13],当性能退化量首次超过失效阈值
| $T = \inf \left\{ {t:X\left( t \right) \geqslant \omega \left| {X(0) < \omega } \right.} \right\}$ | (2) |
失效阈值
| ${L_k} = \inf \left\{ {{l_k}:X\left( {{l_k} + {t_k}} \right) \geqslant \omega \left| {X\left( {{t_k}} \right) < \omega } \right.} \right\}$ | (3) |
基于以上假设,对于此类存在变点的随机退化系统可以建立两阶段Wiener过程退化模型:
| $X\left( t \right) = \left\{ {\begin{aligned} &{{x_0} + {\mu _1}t + {\sigma _1}B(t),\;\;\;\;\;\;\;\;\;\;\;0 < t \leqslant \tau }\\ &{{x_\tau } + {\mu _2}(t - \tau ) + {\sigma _2}B(t - \tau ),\;\;\;\;\;\;\;\;\;\;t > \tau } \end{aligned}} \right.$ | (4) |
其中,
在工程实际中,受产品材料、制造工艺差异和工作环境变化等因素的影响,同批次产品的退化特性通常会存在个体差异性[1],即退化轨迹有较大相似性,但是各个产品的退化数据对应的退化率是不一样的。为反映这种样本间差异性所导致的随机效应,在此采用文献[11, 14]中的方法,将退化模型中相关参数随机化,定义式(4)中漂移系数
| $ {f_{\rm{T}}}(t) = \left\{ {\begin{aligned} &\frac{\omega - {x_0}}{{\sqrt {2\pi {t^3}\left( {\sigma _{\rm{\alpha }}^2t + \sigma _1^2} \right)} }}\cdot\\ &\quad\exp \left[ { - \frac{{{{(\omega - {x_0} - {\mu _{\rm{\alpha }}}t)}^2}}}{{2t\left( {\sigma _{\rm{\alpha }}^2t + \sigma _1^2} \right)}}} \right],\;\;\quad\quad\;\;\quad\quad0 < t \leqslant \tau \\ &{\frac{{\omega - {x_\tau }}}{{\sqrt {2\pi {{(t - \tau )}^3}\left[ {\sigma _{\rm{\beta }}^2(t - \tau ) + \sigma _2^2} \right]} }} \cdot }\\ &\quad{\exp \left[ { - \frac{{{{(\omega - {x_\tau } - {\mu _{\rm{\beta }}}(t - \tau ))}^2}}}{{2\sigma _{\rm{\beta }}^2{{(t - \tau )}^2} + 2\sigma _2^2(t - \tau )}}} \right],}\;\;\;\;\;\;\;\;t > \tau \end{aligned}} \right. $ | (5) |
事实上,在变点未出现时,变点处的退化量是未知的,这对计算第一阶段寿命的PDF没有影响。但是在计算第二阶段寿命的PDF时,根据首达时间的概念,要计算退化过程在
首先假设系统在变点发生前就已经失效,即寿命
系统在经历变点后失效,即寿命
引理1[16] 对于两阶段退化过程,如果漂移系数
| $\begin{split} &{f_{\rm{T}}}(t) = \int_{ - \infty }^\omega {\displaystyle\frac{{\omega - {x_\tau }}}{{\sqrt {2\pi {{(t - \tau )}^3}\left[ {\sigma _{\rm{\beta }}^2(t - \tau ) + \sigma _2^2} \right]} }}} \cdot \\ &\quad\exp \left[ { - \displaystyle\frac{{{{(\omega - {x_\tau } - {\mu _{\rm{\beta }}}(t - \tau ))}^2}}}{{2\sigma _{\rm{\beta }}^2{{(t - \tau )}^2} + 2\sigma _2^2(t - \tau )}}} \right]{g_\tau }({x_\tau }|{\mu _{\rm{\alpha }}},{\sigma _{\rm{\alpha }}}){\rm{d}}{x_\tau }=\\ &\quad \displaystyle\int_{ - \infty }^\omega {\displaystyle\frac{{\omega - {x_\tau }}}{{\sqrt {2\pi {{(t - \tau )}^2}\sigma _{\rm{b}}^2} }}\exp \left[ { - \displaystyle\frac{{{{(\omega - {x_\tau } - {\mu _{\rm{b}}})}^2}}}{{2\sigma _{\rm{b}}^2}}} \right]} \cdot \\ &\quad\left[ {1 - \exp \left( { - \displaystyle\frac{{4{\omega ^2} - 4{x_\tau }\omega }}{{2{\sigma _1}^2\tau }}} \right)} \right]\displaystyle\frac{1}{{\sqrt {2\pi \sigma _{\rm{a}}^2} }}\cdot\\ &\quad\exp \left[ { - \displaystyle\frac{{{{({x_\tau } - {\mu _\alpha }\tau )}^2}}}{{2\sigma _{\rm{a}}^2}}} \right]{\rm{d}}{x_\tau } = {{A}} - {{B}} \end{split}$ | (6) |
其中:
| $\begin{array}{c} {\mu _{\rm{a}}} = \omega - {\mu _{\rm{\alpha }}}, \; {\mu _{\rm{c}}} = - \omega - {\mu _{\rm{\alpha }}}\tau - \sigma _{\rm{\alpha }}^2\tau /\sigma _1^2\\ {\mu _{\rm{b}}} = {\mu _{\rm{\beta }}}\left( {t - \tau } \right), \; \sigma _{\rm{a}}^2 = \sigma _{\rm{\alpha }}^2{\tau ^2} + \sigma _1^2\tau \\ \sigma _{\rm{b}}^2 = \sigma _{\rm{\beta }}^2{(t - \tau )^2} + \sigma _2^2(t - \tau )\\ {{A = }}\displaystyle\frac{1}{{\sqrt {2\pi {{(t - \tau )}^2}\left( {\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2} \right)} }}\exp \left[ { - \displaystyle\frac{{{{\left( {{\mu _{\rm{b}}} - {\mu _{\rm{a}}}} \right)}^2}}}{{2\left( {\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2} \right)}}} \right] \cdot \\ \;\;\;\;\;\;\left\{ {\displaystyle\frac{{{\mu _{\rm{a}}}\sigma _{\rm{b}}^2 + {\mu _{\rm{b}}}\sigma _{\rm{a}}^2}}{{\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2}}\varPhi \left( {\displaystyle\frac{{{\mu _{\rm{a}}}\sigma _{\rm{b}}^2 + {\mu _{\rm{b}}}\sigma _{\rm{a}}^2}}{{\sqrt {\sigma _{\rm{a}}^2\sigma _{\rm{b}}^2\left( {\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2} \right)} }}} \right) + } \right.\\ \left. {\;\;\;\;\;\;\sqrt {\displaystyle\frac{{\sigma _{\rm{a}}^2\sigma _{\rm{b}}^2}}{{\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2}}} \phi \left( {\displaystyle\frac{{{\mu _{\rm{a}}}\sigma _{\rm{b}}^2 + {\mu _{\rm{b}}}\sigma _{\rm{a}}^2}}{{\sqrt {\sigma _{\rm{a}}^2\sigma _{\rm{b}}^2\left( {\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2} \right)} }}} \right)} \right\}\\ {{B}} = \exp \left( {\displaystyle\frac{{2{\mu _{\rm{\alpha }}}\omega }}{{\sigma _1^2}} + \displaystyle\frac{{2\sigma _{\rm{\alpha }}^2{\omega ^2}}}{{\sigma _1^4}}} \right) \cdot \\ \;\;\;\;\;\;\displaystyle\frac{1}{{\sqrt {2\pi {{(t - \tau )}^2}\left( {\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2} \right)} }}\exp \left[ { - \displaystyle\frac{{{{\left( {{\mu _{\rm{b}}} - {\mu _{\rm{c}}}} \right)}^2}}}{{2\left( {\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2} \right)}}} \right] \cdot \\ \;\;\;\;\;\;\left\{ {\displaystyle\frac{{{\mu _{\rm{c}}}\sigma _{\rm{b}}^2 + {\mu _{\rm{b}}}\sigma _{\rm{a}}^2}}{{\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2}}\varPhi \left( {\displaystyle\frac{{{\mu _{\rm{c}}}\sigma _{\rm{b}}^2 + {\mu _{\rm{b}}}\sigma _{\rm{a}}^2}}{{\sqrt {\sigma _{\rm{a}}^2\sigma _{\rm{b}}^2\left( {\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2} \right)} }}} \right) + } \right.\\ \left. {\;\;\;\;\;\;\sqrt {\displaystyle\frac{{\sigma _{\rm{a}}^2\sigma _{\rm{b}}^2}}{{\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2}}} \phi \left( {\displaystyle\frac{{{\mu _{\rm{c}}}\sigma _{\rm{b}}^2 + {\mu _{\rm{b}}}\sigma _{\rm{a}}^2}}{{\sqrt {\sigma _{\rm{a}}^2\sigma _{\rm{b}}^2\left( {\sigma _{\rm{a}}^2 + \sigma _{\rm{b}}^2} \right)} }}} \right)} \right\} \end{array}$ | (7) |
若已知当前时刻
情况1:当前时刻
1) 在变点前失效,此时剩余寿命PDF为
| ${f_L}\left( {{l_k}} \right) = \frac{{\omega - {x_k}}}{{\sqrt {2\pi {l_k}^3\left( {\sigma _{\rm{\alpha }}^2{l_k} + \sigma _1^2} \right)} }}\exp \left[ { - \frac{{{{(\omega - {x_k} - {\mu _{\rm{\alpha }}}{l_k})}^2}}}{{2{l_k}\left( {\sigma _{\rm{\alpha }}^2{l_k} + \sigma _1^2} \right)}}} \right]$ | (8) |
2) 在变点后失效,即
情况2:当前时刻
| ${f_L}\left( {{l_k}} \right) = \frac{{\omega - {x_k}}}{{\sqrt {2\pi {l_k}^3\left( {\sigma _{\rm{\beta }}^2{l_k} + \sigma _2^2} \right)} }}\exp \left[ { - \frac{{{{(\omega - {x_k} - {\mu _{\rm{\beta }}}{l_k})}^2}}}{{2{l_k}\left( {\sigma _{\rm{\beta }}^2{l_k} + \sigma _2^2} \right)}}} \right]$ | (9) |
假设存在同一批的n个随机退化设备,分别对应了n组退化数据,即
假设变点的发生时间已知且仅在采样时刻取值,即
| $\begin{array}{l} {\rm{ln}}L\left( {{\mu _{1,i}},{\sigma _1},{\mu _{2,i}},{\sigma _2}|{X_i}} \right) = \\ \;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} \displaystyle\sum\limits_{j = 1}^{{{\tilde \tau }_i}} {{\rm{ln}}\displaystyle\frac{1}{{\sqrt {2\pi \sigma _1^2\Delta t} }}} \exp \left[ {\displaystyle\frac{{{{({x_{i,j}} - {x_{i,j - 1}} - {\mu _{1,i}}\Delta t)}^2}}}{{2\sigma _1^2\Delta t}}} \right] + \\ \;\;\;\;\displaystyle\sum\limits_{j = {{\tilde \tau }_i} + 1}^{{m_i}} {{\rm{ln}}\displaystyle\frac{1}{{\sqrt {2\pi \sigma _2^2\Delta t} }}} \exp \left[ {\displaystyle\frac{{{{({x_{i,j}} - {x_{i,j - 1}} - {\mu _{2,i}}\Delta t)}^2}}}{{2\sigma _2^2\Delta t}}} \right] \end{array}$ | (10) |
其中,
| $\hat \varTheta = \mathop {\operatorname{argmax} }\limits_\varTheta \sum\limits_{i = 1}^n {{\rm{ln}}L\left( {{\mu _{1,i}},{\sigma _1},{\mu _{2,i}},{\sigma _2}|{{X}_i}} \right)} $ | (11) |
其中
| $\begin{array}{l} {\rm{ln}}L\left( {\varTheta |{X},{Z}} \right) = {\rm{In}}\prod\limits_{i = 1}^n {p\left( {{{X}_i},{{Z}_i}|\varTheta } \right)} \\ \;\;\;\; = \sum\limits_{i = 1}^n {{\rm{ln}}\left( {p\left( {{{ Z}_i}|\varTheta } \right)p\left( {{{X}_i}|{{Z}_i},\varTheta } \right)} \right)} \end{array}$ | (12) |
其中
E步:计算
| $\begin{array}{l} Q\left( {\varTheta |{{\hat \varTheta }^{\left( k \right)}}} \right) = {\mathbb{E}_{{Z}|{X},{{\hat \varTheta }^{\left( k \right)}}}}\left[ {\ln p\left( {{X},{Z}|\varTheta } \right)} \right] \\ \;\;\;\; = {\mathbb{E}_{{Z}|{X},{{\hat \varTheta }^{\left( k \right)}}}}\sum\limits_{i = 1}^n {\ln \left[ {p\left( {{{Z}_i}|\varTheta } \right)p\left( {{{X}_i}|{{Z}_i},\varTheta } \right)} \right]} \\ \end{array} $ | (13) |
其中,
M步:计算
下面给出第k+1步的参数估计结果:
| $ \begin{array}{l} {\hat \mu _{\rm{\alpha }}}^{\left( {k + 1} \right)} = \displaystyle\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\displaystyle\frac{{\left( {{x_{i,{{\tilde \tau }_i}}} - {x_{i,0}}} \right)\Delta t{\sigma _{\rm{\alpha }}}{{^{2,}}^{\left( k \right)}} + {{\hat \sigma }_1}{{^{2,}}^{\left( k \right)}}\Delta t{\mu _{\rm{\alpha }}}^{\left( k \right)}}}{{{{\tilde \tau }_i}{\sigma _{\rm{\alpha }}}{{^{2,}}^{\left( k \right)}}\Delta {t^2} + {{\hat \sigma }_1}{{^{2,}}^{\left( k \right)}}\Delta t}}} \\ {\hat \sigma _{\rm{\alpha }}}^{2,\left( {k + 1} \right)} = \displaystyle\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n{\left( {\mathbb{E}\left[ {\mu _{1,i}^2|{{X}_i},{{\hat \varTheta }^{\left( k \right)}}} \right] - {\mathbb{E}^2}\left[ {{\mu _{1,i}}|{{X}_i},{{\hat \varTheta }^{\left( k \right)}}} \right]} \right)} \\ {\hat \mu _{\rm{\beta }}}^{\left( {k + 1} \right)} = \displaystyle\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n{\displaystyle\frac{{\left( {{x_{i,{m_i}}} - {x_{i,{{\tilde \tau }_i} - 1}}} \right)\Delta t{\sigma _{\rm{\beta }}}{{^{2,}}^{\left( k \right)}} + {{\hat \sigma }_2}{{^{2,}}^{\left( k \right)}}\Delta t{\mu _{\rm{\beta }}}^{\left( k \right)}}}{{\left( {{m_i} - {{\tilde \tau }_i}} \right){\sigma _{\rm{\beta }}}{{^{2,}}^{\left( k \right)}}\Delta {t^2} + {{\hat \sigma }_2}{{^{2,}}^{\left( k \right)}}\Delta t}}} \\ {\hat \sigma _{\rm{\beta }}}^{2,\left( {k + 1} \right)} = \displaystyle\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n{\left( {\mathbb{E}\left[ {\mu _{2,i}^2|{{X}_i},{{\hat \varTheta }^{\left( k \right)}}} \right] - {\mathbb{E}^2}\left[ {{\mu _{2,i}}|{{X}_i},{{\hat \varTheta }^{\left( k \right)}}} \right]} \right)} \\ {\hat \sigma _1}^{2,\left( {k + 1} \right)} =\\ \frac{{\displaystyle\sum\limits_{i = 1}^n {\left\{ \begin{array}{l} \displaystyle\sum\limits_{j = 1}^{{{\tilde \tau }_i}} {{{\left( {{x_{i,j}} - {x_{i,j - 1}}} \right)}^2} + {{\tilde \tau }_i}\mathbb{E}\left[ {\mu _{1,i}^2|{{X}_i},{{\hat \varTheta }^{\left( k \right)}}} \right] - } \\ 2\mathbb{E}\left[ {{\mu _{1,i}}|{{X}_i},{{\hat \varTheta }^{\left( k \right)}}} \right]\displaystyle\sum\limits_{j = 1}^{{{\tilde \tau }_i}} {\left( {{x_{i,j}} - {x_{i,j - 1}}} \right)} \\ \end{array} \right\}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{\tilde \tau }_i}\Delta t} }} \\ {\hat \sigma _2}^{2,\left( {k + 1} \right)} = \\\displaystyle \frac{{\displaystyle\sum\limits_{i = 1}^n {\left\{ \begin{array}{l} \displaystyle\sum\limits_{j = {{\tilde \tau }_i} + 1}^{{m_i}} {{{\left( {{x_{i,j}} - {x_{i,j - 1}}} \right)}^2} + \left( {{m_i} - {{\tilde \tau }_i}} \right)\mathbb{E}\left[ {\mu _{2,i}^2|{{X}_i},{{\hat \varTheta }^{\left( k \right)}}} \right]} \\ - 2\mathbb{E}\left[ {{\mu _{2,i}}|{{X}_i},{{\hat \varTheta }^{\left( k \right)}}} \right]\displaystyle\sum\limits_{j = {{\tilde \tau }_i} + 1}^{{m_i}} {\left( {{x_{i,j}} - {x_{i,j - 1}}} \right)} \\ \end{array} \right\}} }}{{\displaystyle\sum\limits_{i = 1}^n {\left( {{m_i} - {{\tilde \tau }_i}} \right)\Delta t} }} \end{array} $ | (14) |
由EM算法的性质可知,最后退化模型的参数估计是收敛的,通过迭代E步和M步直到满足某一收敛判据时终止,由此得到对应的参数估计值。
3.2 基于贝叶斯理论的在线参数更新在本小节中,主要针对某一运行中的退化设备,如何根据离线参数估计得到的先验信息和当前运行信息来更新参数估计结果。定义当前时间为
令
| $p\left( {{\mu _1}|{{X}_{0:k}}} \right) \propto p\left( {{{X}_{0:k}}|{\mu _1}} \right)p\left( {{\mu _1}} \right)$ | (15) |
其中:
| $p\left( {{{X}_{0:k}}|{\mu _1}} \right) = \prod\limits_{i = 1}^k {\frac{1}{{\sqrt {2\pi \sigma _1^2\Delta t} }}\exp \left[ { - \frac{{{{({x_i} - {x_{i - 1}} - {\mu _1}\Delta t)}^2}}}{{2\sigma _1^2\Delta t}}} \right]} $ | (16) |
| $p\left( {{\mu _1}} \right) = \frac{1}{{\sqrt {2\pi \sigma _{{\rm{\alpha }},0}^2} }}\exp \left[ { - \frac{{{{({\mu _1} - {\mu _{{\rm{\alpha }},0}})}^2}}}{{2\sigma _{{\rm{\alpha }},0}^2}}} \right]$ | (17) |
由于
| $p\left( {{\mu _1}|{{X}_{0:k}}} \right) = \frac{1}{{\sqrt {2\pi \sigma _{\rm{\alpha }}^2} }}\exp \left[ { - \frac{{{{({\mu _1} - {\mu _{\rm{\alpha }}})}^2}}}{{2\sigma _{\rm{\alpha }}^2}}} \right]$ | (18) |
| ${\mu _{\rm{\alpha }}} = \frac{{{\mu _{{\rm{\alpha }},0}}\sigma _1^2 + \left( {{x_k} - {x_0}} \right)\sigma _{{\rm{\alpha }},0}^2}}{{\left( {{t_k} - {t_0}} \right)\sigma _{{\rm{\alpha }},0}^2 + \sigma _1^2}}$ | (19) |
| $\sigma _{\rm{\alpha }}^2 = \frac{{\sigma _1^2\sigma _{{\rm{\alpha }},0}^2}}{{\left( {{t_k} - {t_0}} \right)\sigma _{{\rm{\alpha }},0}^2 + \sigma _1^2}}$ | (20) |
类似地,若
| $p\left( {{\mu _2}|{{X}_{\tilde \tau :k}}} \right) = \frac{1}{{\sqrt {2\pi \sigma _{\rm{\beta }}^2} }}\exp \left[ { - \frac{{{{({\mu _2} - {\mu _{\rm{\beta }}})}^2}}}{{2\sigma _{\rm{\beta }}^2}}} \right]$ | (21) |
| ${\mu _{\rm{\beta }}} = \frac{{{\mu _{{\rm{\beta }},0}}\sigma _2^2 + \left( {{x_k} - {x_{\tilde \tau }}} \right)\sigma _{{\rm{\beta }},0}^2}}{{\left( {{t_k} - {t_{\tilde \tau }}} \right)\sigma _{{\rm{\beta }},0}^2 + \sigma _2^2}}$ | (22) |
| $\sigma _{\rm{\beta }}^2 = \frac{{\sigma _2^2\sigma _{{\rm{\beta }},0}^2}}{{\left( {{t_k} - {t_{\tilde \tau }}} \right)\sigma _{{\rm{\beta }},0}^2 + \sigma _2^2}}$ | (23) |
本文所提方法在应用场景下模型参数的离线估计和在线更新以及设备可靠性评估步骤流程如图1所示。
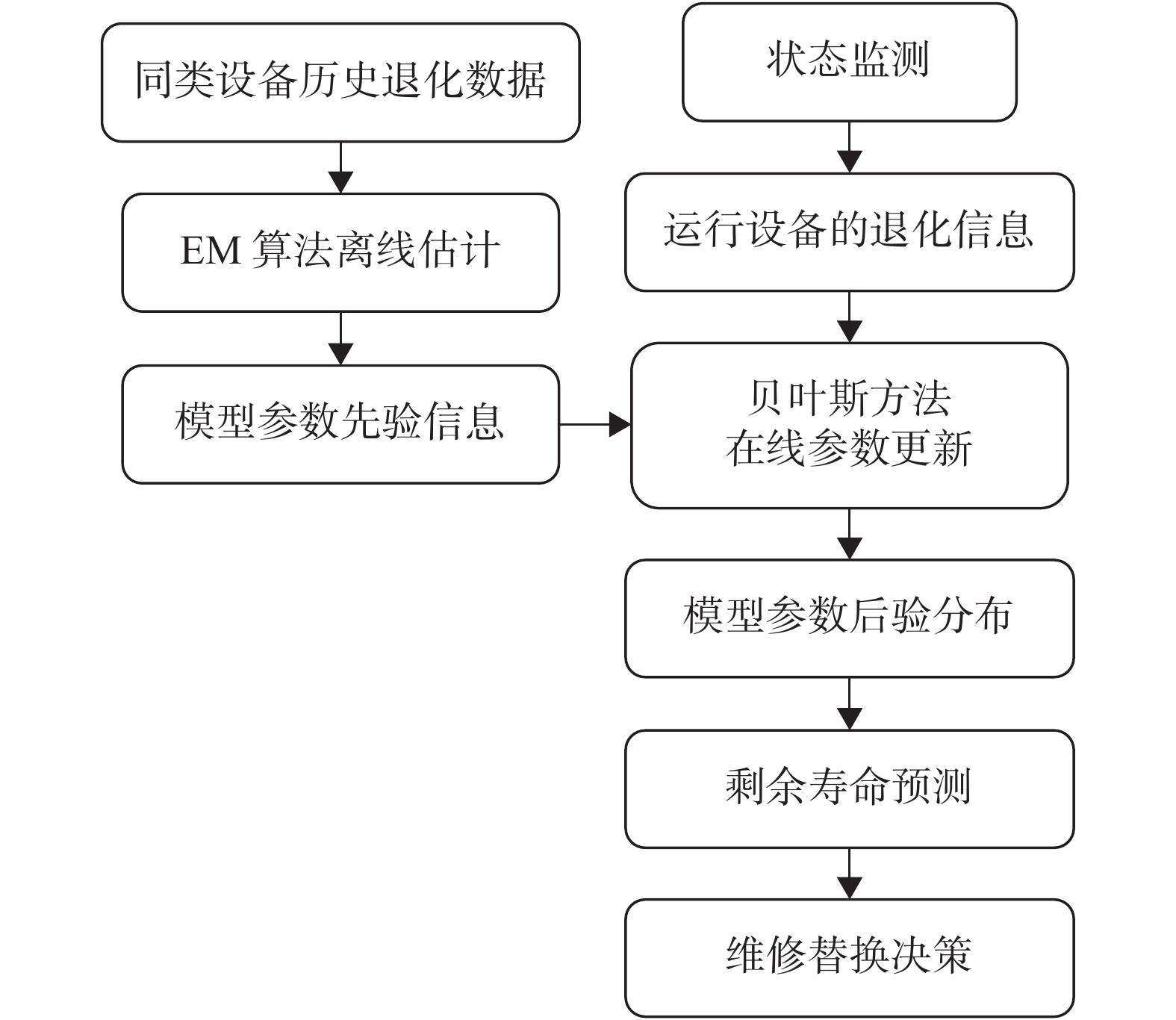
|
| 图 1 设备参数估计更新和寿命预测的步骤流程图 |
以液力耦合器为研究对象,按照上述设备模型参数的估计更新以及寿命预测的步骤,对文中提出的模型进行实例研究。图2描述了5台液力耦合器的振幅随时间的变化情况[3]。从图中可以看出,退化数据呈现出明显的两阶段退化特征。本文采用LCD1、LCD3、LCD4、LCD5 4组数据用于离线参数估计,并将估计得到的模型参数作为先验信息用于之后的在线参数更新和剩余寿命预测。此外,假设LCD2的退化数据作为当前设备的运行信息用于在线参数更新和剩余寿命预测的校验。
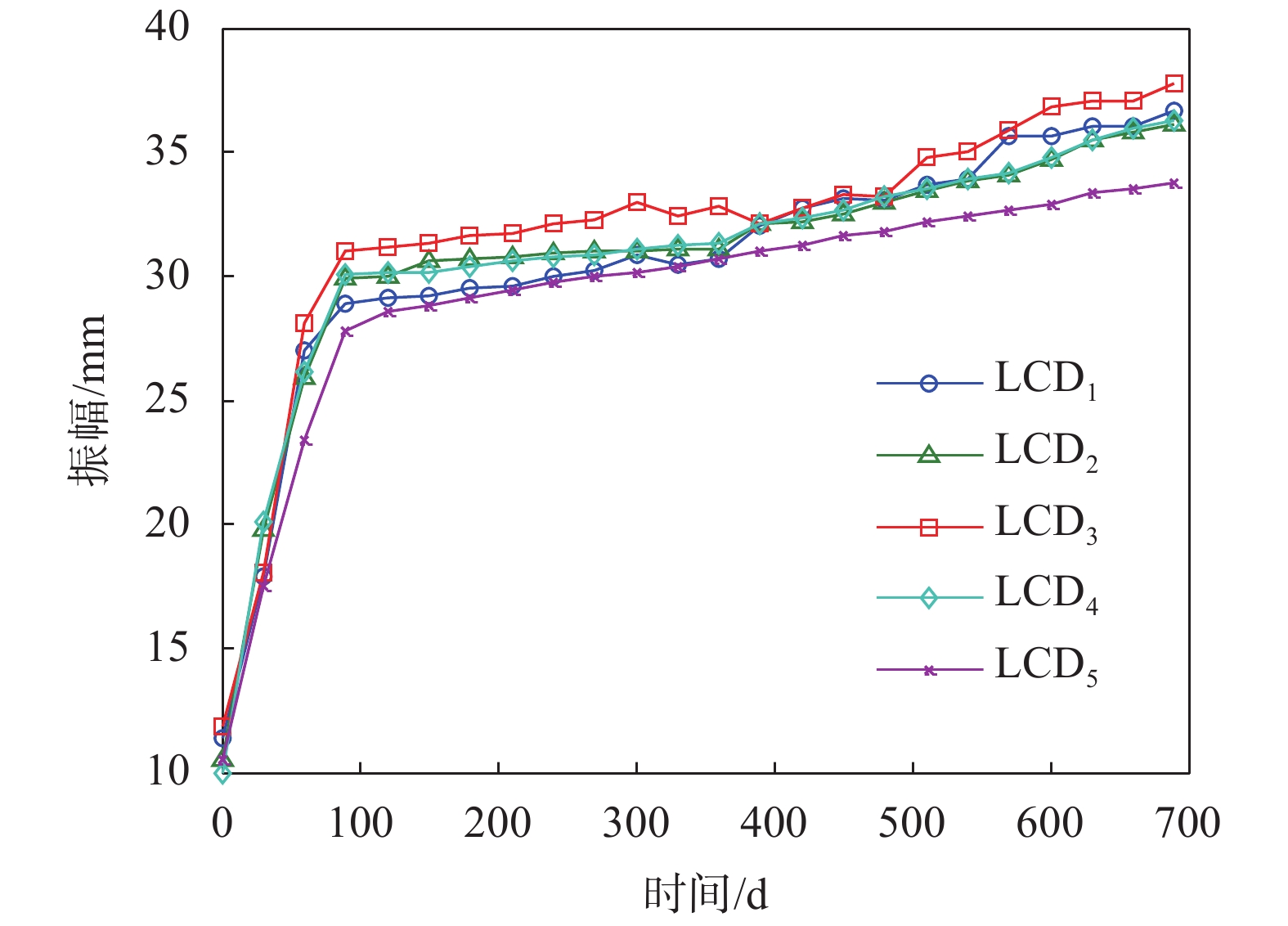
|
| 图 2 液力耦合器的振幅随时间发生退化 |
首先,根据EM算法离线估计得到参数
如图3所示,蓝线表示在EM算法中给定的100组不同的模型参数初值,绿线表示最终迭代结果,最终模型参数均收敛至如下结果:
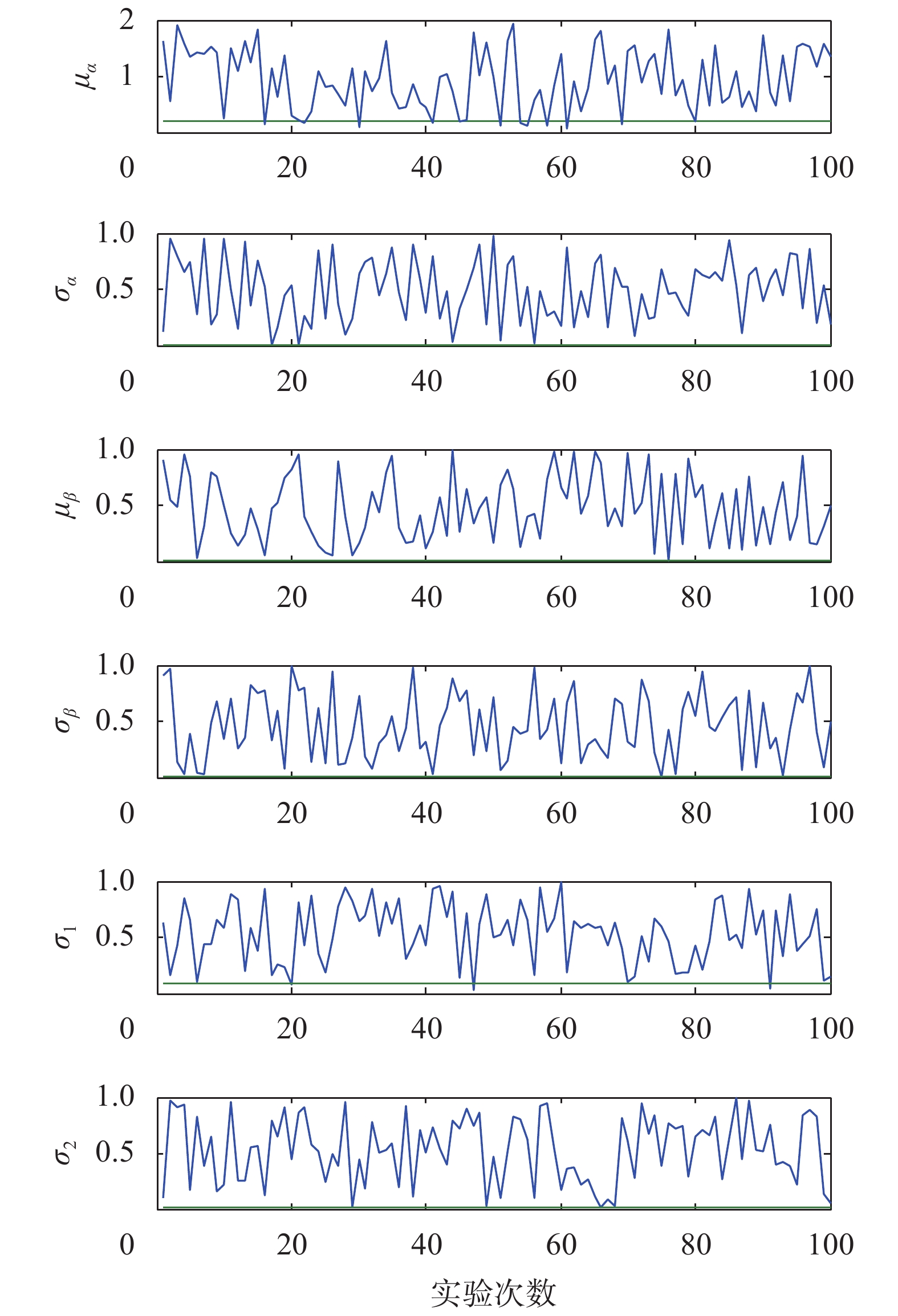
|
| 图 3 EM算法中模型参数的初值与终值 |
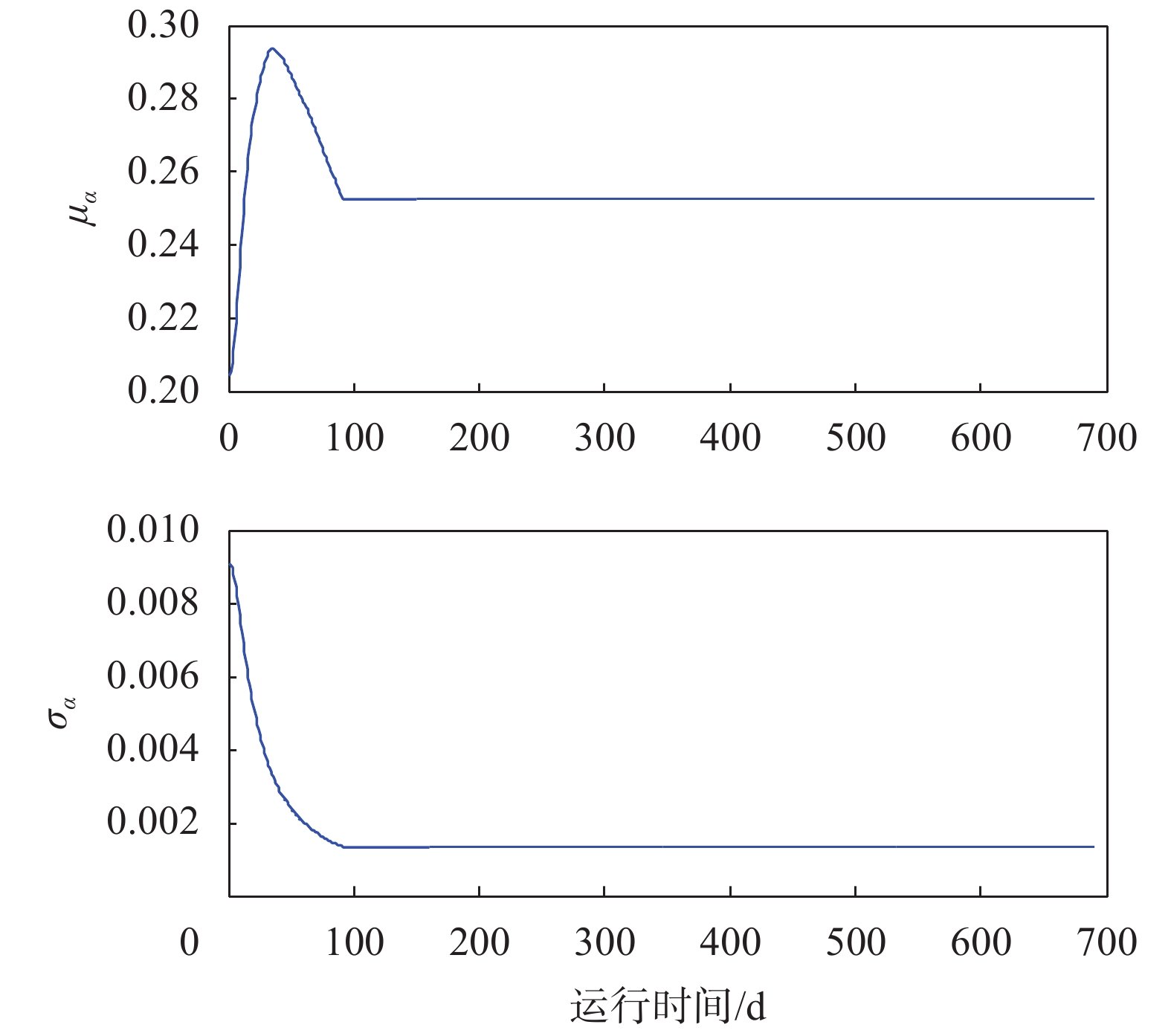
|
| 图 4 第一阶段模型参数的更新过程 |
|
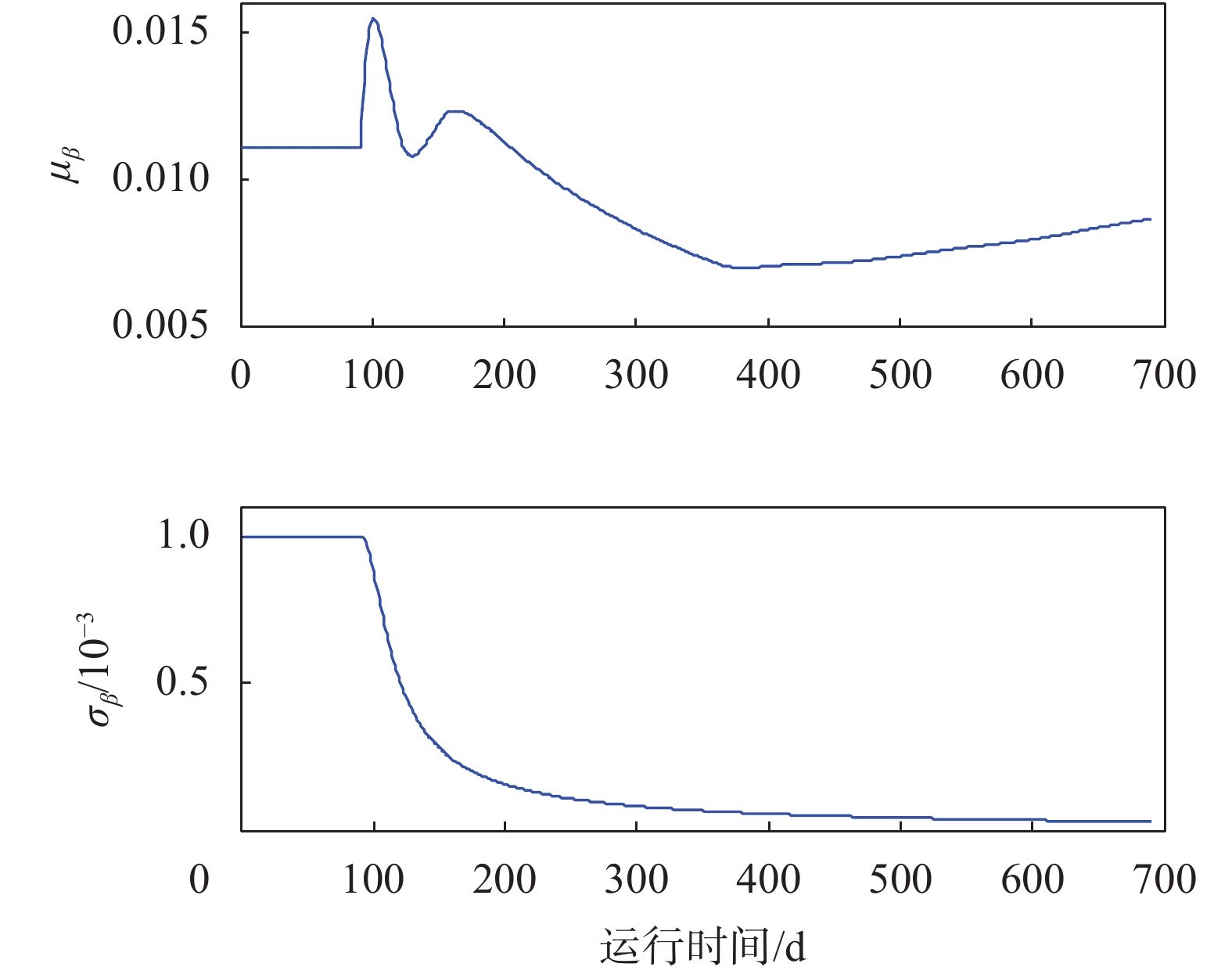
| 图 5 第二阶段模型参数的更新过程 |
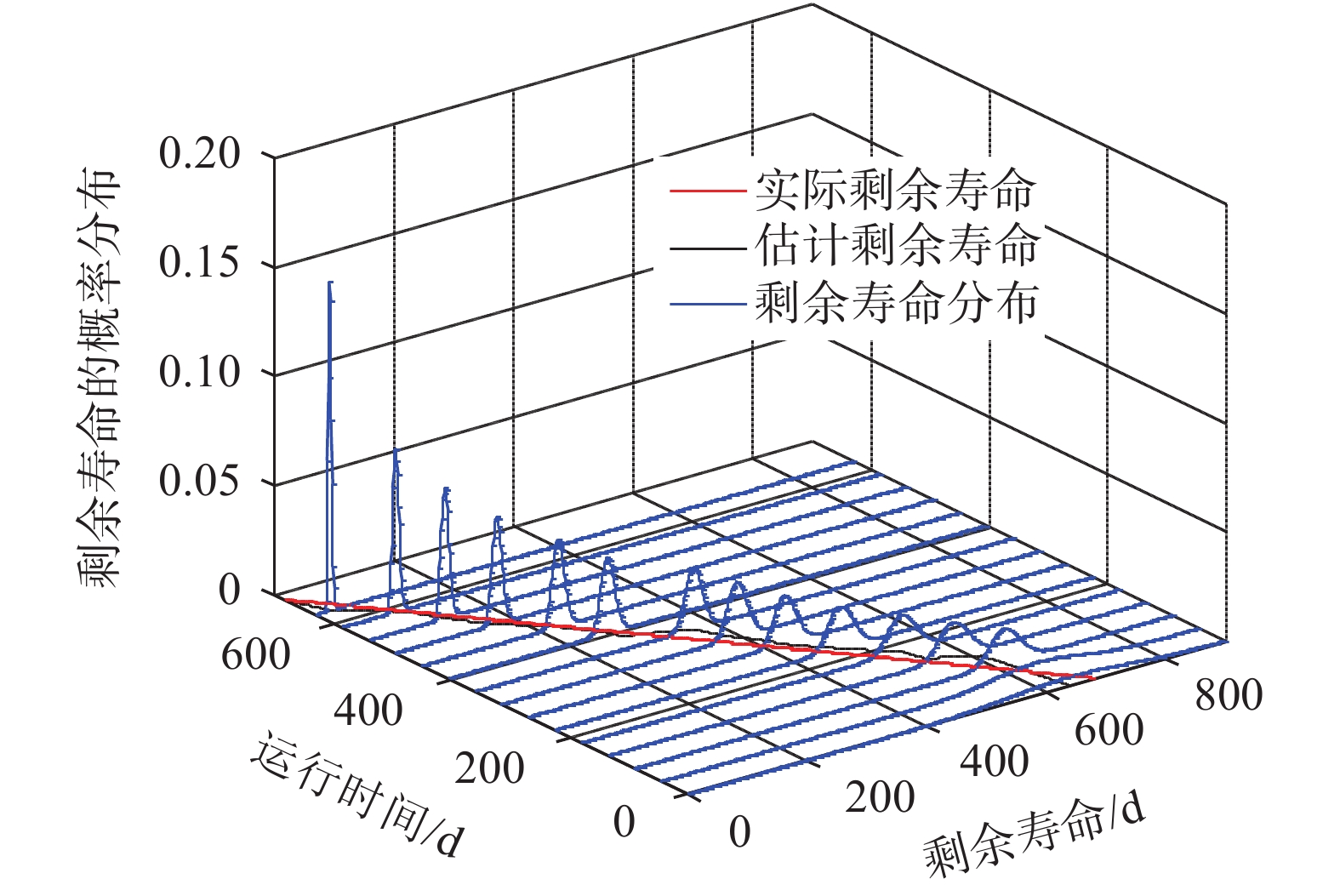
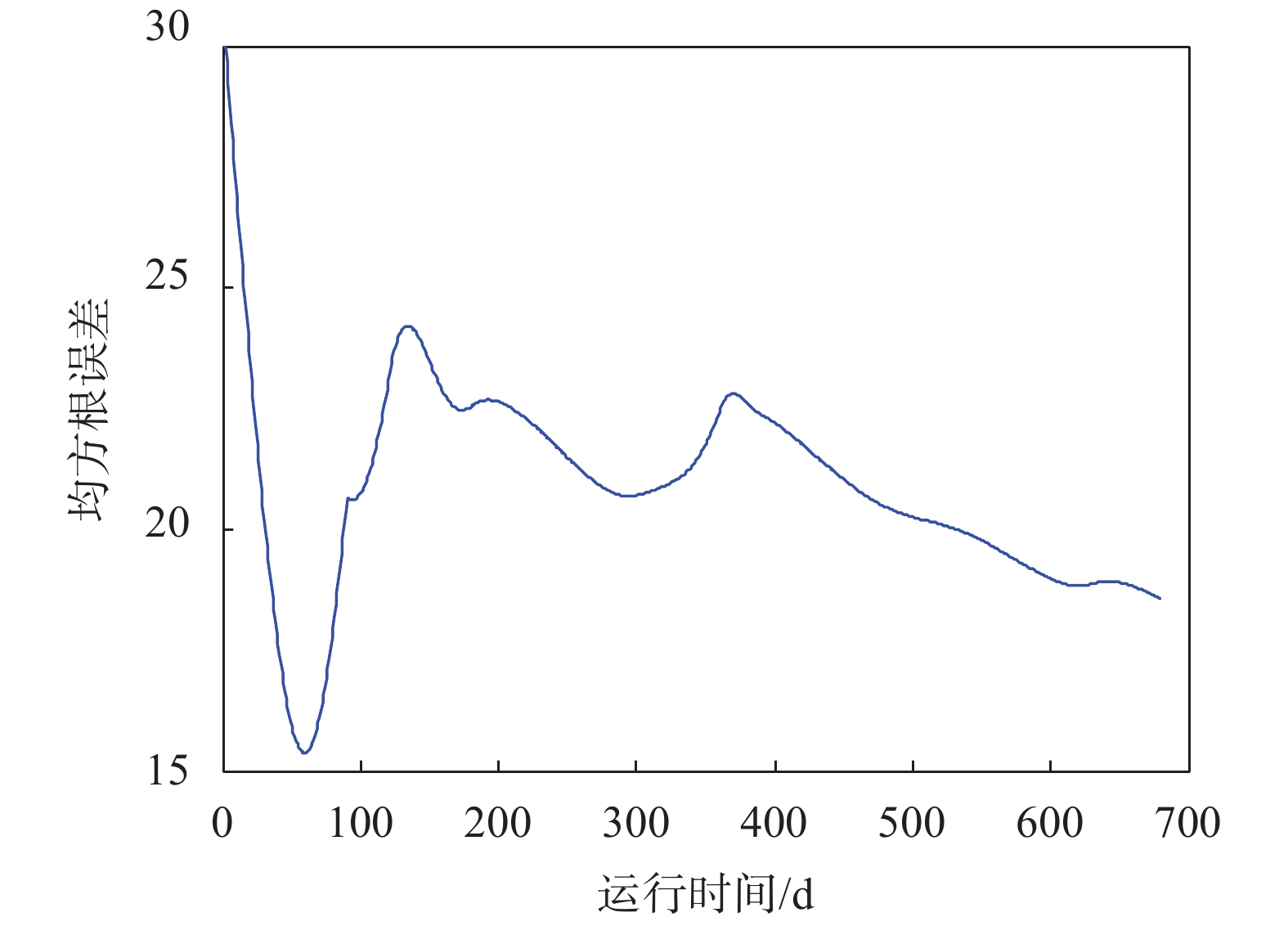
接下来,根据在线参数估计的结果,对剩余寿命进行估计。规定当振动振幅超过阈值36 mm时,液力耦合器发生失效。LCD2的剩余寿命预测结果和均方根误差如图6、图7所示。从中可以看出,本文所提方法能够有效预测LCD的剩余寿命。整体上看,随着运行时间的增加,寿命预测结果愈加精确,但当退化率发生较大波动时,预测结果误差稍有增大。在图7中反映为从330~390 d,均方根误差有增大趋势,当退化率稳定波动较小时,误差不断减小。根据寿命预测结果,为保证设备的运行可靠性,在设备失效前及时对设备进行维修替换活动,从而避免财产损失和事故发生。
|
| 图 6 LCD2剩余寿命预测结果 |
|
| 图 7 LCD2剩余寿命均方根误差 |
5 结束语
本文结合工程实践中设备退化过程存在变点,变点前后退化特征显著差异的问题建立了两阶段维纳过程退化模型进行剩余寿命预测研究,重点阐述了模型参数的离线辨识和在线更新算法,最后通过液力耦合器实验数据验证了其可行性和有效性。
1) 引入随机参数描述样本间差异性,得到首达时间意义下两阶段系统剩余寿命分布的解析表达形式,实现剩余寿命的在线实时估计。
2) 提出基于EM算法的参数离线辨识和基于贝叶斯理论的参数在线更新算法,实现设备的实时可靠性评估,为维修替换决策提供依据。
本文研究的两阶段退化模型是多阶段模型的基础,基于多阶段模型的退化建模与剩余寿命预测问题可在本文研究结论的基础上拓展推广得到。下一步工作将继续研究多阶段退化问题以提高方法的普适性和应用价值。
| [1] |
SI X S, WANG W, HU C H, et al. Remaining useful life estimation-a review on the statistical data driven approaches[J].
European Journal of Operational Research, 2011, 213(1): 1-14.
DOI:10.1016/j.ejor.2010.11.018 |
| [2] |
ZHOU R S, SERBAN N, GEBRAEEL N. Degradation-based residual life prediction under different environments[J].
The Annals of Applied Statistics, 2014, 8(3): 1671-1689.
DOI:10.1214/14-AOAS749 |
| [3] |
WANG X, JIANG P, GUO B, et al. Real-time reliability evaluation for an individual product based on change-point gamma and Wiener process[J].
Quality and Reliability Engineering International, 2014, 30(4): 513-525.
DOI:10.1002/qre.v30.4 |
| [4] |
NG T S. An application of the EM algorithm to degradation modeling[J].
IEEE Transactions on Reliability, 2008, 57(1): 2-13.
DOI:10.1109/TR.2008.916867 |
| [5] |
YUAN T, BAE S J, ZHU X. A Bayesian approach to degradation-based burn-in optimization for display products exhibiting two-phase degradation patterns[J].
Reliability Engineering & System Safety, 2016, 155(11): 55-63.
|
| [6] |
BAE S J, KVAM P H. A change-point analysis for modeling incomplete burn-in for light displays[J].
IIE Transactions, 2006, 38(3): 489-498.
DOI:10.1080/074081791009068 |
| [7] |
WANG P, TANG Y, BAE S J, et al. Bayesian analysis of two-phase degradation data based on change-point Wiener process[J].
Reliability Engineering & System Safety, 2018, 170(2): 244-256.
|
| [8] |
王前程, 陈云霞, 康锐. 加速度计加速退化机理模型建模方法[J].
北京航空航天大学学报, 2012, 38(10): 1405-1409.
|
| [9] |
BURGESS W L. Valve regulated lead acid battery float service life estimation using a Kalman filter[J].
Journal of Power Sources, 2009, 191(1): 16-21.
DOI:10.1016/j.jpowsour.2008.12.123 |
| [10] |
CHEN N, TSUI K L. Condition monitoring and remaining useful life prediction using degradation signals: Revisited[J].
IIE Transactions, 2013, 45(9): 939-952.
DOI:10.1080/0740817X.2012.706376 |
| [11] |
YAN W A, SONG B W, DUAN G L, et al. Real-time reliability evaluation of two-phase Wiener degradation process[J].
Communications in Statistics-Theory and Methods, 2017, 46(1): 176-188.
DOI:10.1080/03610926.2014.988262 |
| [12] |
BAE S J, YUAN T, NING S, et al. A Bayesian approach to modeling two-phase degradation using change-point regression[J].
Reliability Engineering & System Safety, 2015, 134(2): 66-74.
|
| [13] |
LEE M, WHITMORE G. Threshold regression for survival analysis: modeling eventtimes by a stochastic process reaching a boundary[J].
Statistical Science, 2006, 21(3): 501-513.
|
| [14] |
SI X S, WANG W, CHEN M Y, et al. A degradation path-dependent approach for remaining useful life estimation with an exact and closed-form solution[J].
European Journal of Operational Research, 2013, 226(1): 53-66.
DOI:10.1016/j.ejor.2012.10.030 |
| [15] |
SI X S, WANG W, HU C H, et al. A Wiener process based degradation model with a recursive filter algorithm for remaining useful life estimation[J].
Mechanical Systems and Signal Processing, 2013, 35(1/2): 219-237.
DOI:10.1016/j.ymssp.2012.08.016 |
| [16] |
ZHANG J X, HU C H, ZHOU D H, et al. A novel lifetime estimation method for two-phase degrading systems[J].
IEEE Transactions on Reliability, 2018(6): 1-21.
DOI:10.1109/TR.2018.2829844 |
 2019, Vol. 45
2019, Vol. 45


