文章信息
- 陈雷, 张晓明, 檀杰, 邱江涛
- CHEN Lei, ZHANG Xiaoming, TAN Jie, QIU Jiangtao
- 基于卡尔曼滤波的旋转弹药弹体磁场校正方法
- Calibration method of projectile magnetic field for spinning projectiles based on Kalman filter
- 中国测试, 2019, 45(2): 48-53
- CHINA MEASUREMENT & TEST, 2019, 45(2): 48-53
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018060029
-
文章历史
- 收稿日期: 2018-06-08
- 收到修改稿日期: 2018-07-13
制导弹药精确打击的前提是精确获取高精度的姿态导航信息,地磁姿态系统对常规弹药的制导有着重要意义[1]。地磁姿态系统利用地磁场信息进行载体姿态解算,与惯性系统组合导航,可补偿陀螺漂移,提供全天候、全地域、全天时的导航姿态信息[2]。
捷联地磁姿态系统利用地磁信息进行姿态解算时,作用于磁传感器上的磁场不仅有地磁场信息,还有干扰磁场信息[3]。尽管在弹药设计制造阶段可以通过消磁技术来减少弹体磁场的干扰,但弹体磁场仍可达到数百到数千纳特[4]。而且由于弹体磁场长时间存储磁化以及发射过载下弹体磁场的改变[5],事先标定的干扰磁场参数无法真实反映弹体磁场的变化,进而严重影响姿态解算的精度。因此需要一种实时准确的载体磁场校正方法,以提高地磁场的实时测量精度。
传统的弹体磁场校正方法将磁传感器历史测量值统一处理,事先求解出弹体磁场的校正参数。这类参数估计方法称为事先标定法,有椭圆拟合法[6]、椭球拟合法、超定方程求解最小二乘参数法[7]等。其求解固定磁干扰参数较为准确,但由于需要内存空间大,计算复杂度高,不适用于旋转弹弹体磁场参数的在线校正或弹体磁场参数变化较大的环境。在线弹体磁场的校正方法包括递推最小二乘法、八航向校正法[8]、二步校准法[3]等。递推最小二乘法估计参数方法较适合于机载解算,但算法固有特点导致在弹体磁场参数变化时增益参数会过度收敛[9-10],会使得所估计参数出现误差。而八航向校正法对弹体磁场参数校准模型建模准确性要求高,求解准确磁场校正系数难度较大[11]。二步校准法是通过最小二乘法求取固定磁场和比例因数误差的迭代算法,该算法鲁棒性好,但由于两步估计均为非线性参数估计,估计过程复杂,计算量较大[12]。
为了实现旋转弹药弹体磁场的在线校正,首先分析了旋转弹药弹体干扰磁场误差来源,建立了测量误差模型,最终得到了基于三维磁场的线性观测模型。利用事先标定法为参数辨识提供初始条件,再采用卡尔曼滤波算法(KF)估计误差系数,最终实现了磁测信号的高精度校正。最后进行了一系列的仿真试验和转台试验,验证了弹体磁场校正算法的性能。
1 弹体磁场误差模型 1.1 弹体磁场误差机理定义捷联地磁传感器的弹体坐标系(b系),其坐标原点位于传感器安装位点上,

|
| 图 1 载体坐标系 |
事先标定的校正参数,可以补偿掉地磁传感器的制造误差和安装误差,因此可以将其视为理想的捷联地磁传感器。捷联地磁传感器在弹体坐标系下的量测方程可表示为:
| $ {{H}}_{\rm{m}}^{\rm{b}} = {{{C}}_{\rm{s}}}{{H}}_{\rm{e}}^{\rm{b}} + {{{B}}_0} + {{\zeta }} $ | (1) |
式中:
| $ {{{C}}_{\rm{s}}} = \left[ {\begin{array}{*{20}{c}} {{c_{xx}}}&{{c_{xy}}}&{{c_{xz}}}\\ {{c_{yx}}}&{{c_{yy}}}&{{c_{yz}}}\\ {{c_{zx}}}&{{c_{zy}}}&{{c_{zz}}} \end{array}} \right] $ | (2) |
此外,弹体内部的电子仪器还可能产生时变的干扰磁场,不过单根通电导线产生的电磁场相对较小,可以通过合理布线的方式减小其影响,因此此类干扰磁场基本可以忽略不计。
1.2 弹体捷联磁场测量模型若地磁姿态系统相对位置保持静止,只改变姿态,地磁场矢量的模值
| $ {({{H}}_{\rm{m}}^{\rm{b}})^{\rm{T}}}{{MH}}_{\rm{m}}^{\rm{b}} - 2{{{H}}_0}^{\rm{T}}{{MH}}_{\rm{m}}^{\rm{b}} + {{{H}}_0}^{\rm{T}}{{M}}{{{H}}_0}{{ = }}{\left| {\left| {{{H}}_{\rm{e}}^{\rm{b}}} \right|} \right|^2} $ | (3) |
其中:
弹体干扰磁场下的地磁矢量图如图2所示,地磁场分量
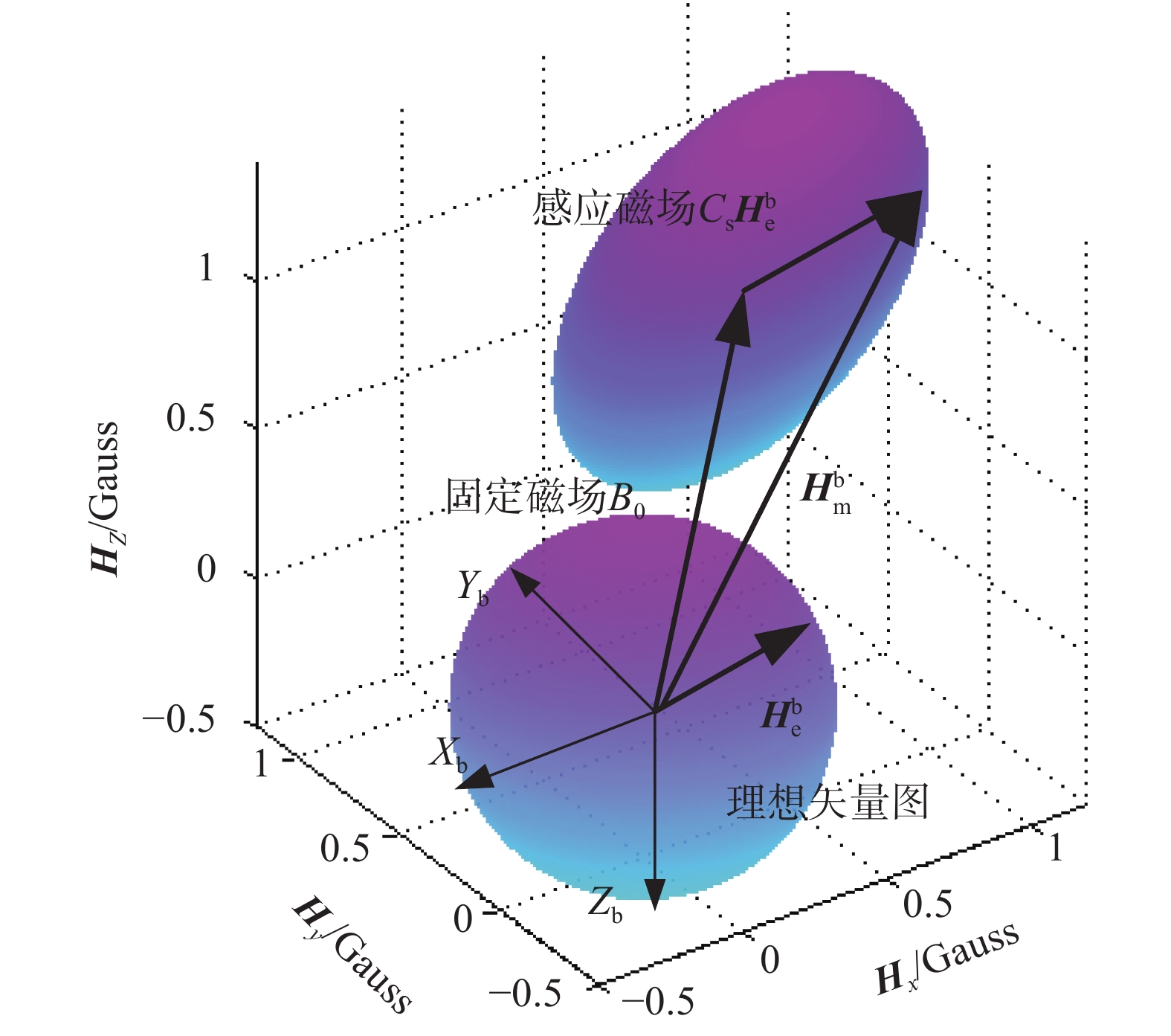
|
| 图 2 弹体干扰磁场对地磁矢量图的影响 |
| $\begin{aligned} a{{H}}_x^2 + b{{H}}_y^2 + c{{H}}_z^2 + d{{{H}}_x}{{{H}}_y} + e{{{H}}_x}{{{H}}_z} + \\g{{{H}}_y}{{{H}}_z} + l{{{H}}_x} + m{{{H}}_y} + n{{{H}}_z} + p = 0 \end{aligned}$ | (4) |
其中:
考虑到噪声误差
首先,滤波器的状态向量取值定义为
| $\left\{ \begin{array}{l} {{{\theta }}_k} = {{{\theta }}_{k - 1}}\\ {{{Z}}_k}={{{H}}_k}{{{\theta }}_k} + {{{V}}_k} \end{array} \right. $ | (5) |
其中:
| $ E\left[ {{{{V}}_k}} \right]=0,\;\;E\left[ {{{{V}}_j}{{{V}}_k}} \right] = {{{R}}_k}{\delta _{kj}} $ | (6) |
根据卡尔曼滤波原理,在线弹体磁场误差系参数辨识的实现步骤为:
1)利用事先标定法确定状态向量和协方差矩阵的初始状态
2)状态预测:
| $ \left\{ \begin{array}{l} {{{{\hat \theta }}}_{k/k - 1}} = {{{{\hat \theta }}}_{k - 1}}\\ {{{{\hat P}}}_{k/k - 1}} = {{{{\hat P}}}_{k - 1}} \end{array} \right. $ | (7) |
3)状态估计:
| $ \left\{ \begin{array}{l} {{{K}}_k} = {{{P}}_{k/k - 1}}{{H}}_k^{\rm T}{({{{H}}_k}{{{P}}_{k/k - 1}}{{H}}_k^{\rm T} + {{{R}}_k})^{ - {\rm T}}}\\ {{{{\hat X}}}_k} = {{{{\hat X}}}_{k/k - 1}} + {{{K}}_k}({{{Z}}_k} - {{{H}}_k}{{{{\hat X}}}_{k/k - 1}})\\ {{{P}}_k} = ({{I}} - {{{K}}_k}{{{H}}_k}){{{P}}_{k/k - 1}} \end{array} \right. $ | (8) |
4)返回到第2个步骤,直到状态向量
| $ \mathop {\max }\limits_{\forall i} \left| {\frac{{{\theta _{k,i}} - {\theta _{k - 1,i}}}}{{{\theta _{k,i}}}}} \right| < \rho ({\text{适当小的数}}) $ | (9) |
时,即当各待估参数变化不大时,可认为参数辨识完毕。
2.2 弹体磁环境的校正上述过程实现了椭球模型状态向量
| $ {{{B}}_0} = {{ - }}\frac{1}{2}{{{M}}^{-1}}{{Q}} $ | (10) |
其中:
由于M是实对称矩阵,对该矩阵进行奇异值分解(singular value decomposition, SVD)可得到M=
| $ {{{C}}^{-1}_{\rm S}}= {{ A }} ={{{U}}^{\rm{T}}}\sqrt {{{{S}}_{{M}}}} {{U}} $ | (11) |
标定的目的在于尽可能消除噪声误差
| $ {{H}}_{\rm e}^{\rm b} = {{{C}}^{ - 1}_{\rm S}}({{H}}_{\rm m}^{\rm b} - {{{B}}_0}) $ | (12) |
利用Matlab环境仿真飞行弹体下的磁测数据,通过一组仿真试验检验了初值选取对弹体磁场校正算法鲁棒性和收敛速度的作用效果,然后通过转台试验验证算法的实时性和有效性。
3.1 仿真分析根据旋转弹药在外弹道无控飞行状态下的运动规律,弹体偏航角近似为零,理想无干扰磁场时捷联三轴磁传感器测量数据的特征为:轴向磁场分量随弹体俯仰变化规律而变化;两个径向磁场呈类正弦变化:频率为弹体滚转角速度,幅值随弹体俯仰变化规律而变化,两者彼此正交。地磁场在载体坐标下的模值
表1给出了仿真试验的试验条件,试验通过常规法和事先标定法分别选取初始条件来评估初值选取对算法性能的影响。根据以往磁测数据,设定干扰磁场下的误差矩阵系数,地磁场测量噪声服从精度为0.000 5 Gauss、均值为零的高斯分布。常规法选取的参数初值均为1,事先标定法选取的初值如表1的试验Ⅱ所示。试验Ⅰ的仿真结果如图3(a)、图3(b)所示,图3(a)显示了参数逐步收敛的全过程,可以看出在初始段参数估计出现了多次较大的震荡,甚至发散。这是由于初始阶段信息量的不足,估计参数无法满足椭球方程的约束条件,从而导致了参数估计过程的大幅震荡。估计参数震荡后的收敛过程如图3(b)所示,可以看出一旦估计参数满足约束条件后,该算法便能使其始终维持在约束条件内,从而在3 s左右逐步完成了参数收敛。图4显示了试验II的仿真结果,可以看出通过事先标定法得到的初始条件在参数估计的一开始就满足约束条件,从而避免了参数估计初始阶段的大幅震荡,而之后除cxx外的各参数更是在1s的时间内完成了收敛过程。
| 试验 | 初始条件
|
固定磁场B0/Gauss | 感应磁场系数Cs | 测量噪声/Gauss |
| Ⅰ | [1 1 1 1 1 1 1 1 1 1]T | [0.1 0.2 0.3]T |
|
0.000 5 |
| Ⅱ | [0.921 –0.08 –0.7 –2 –0.05 0.2 0.5 –0.2]T | [0.1 0.2 0.3]T |
|
0.000 5 |
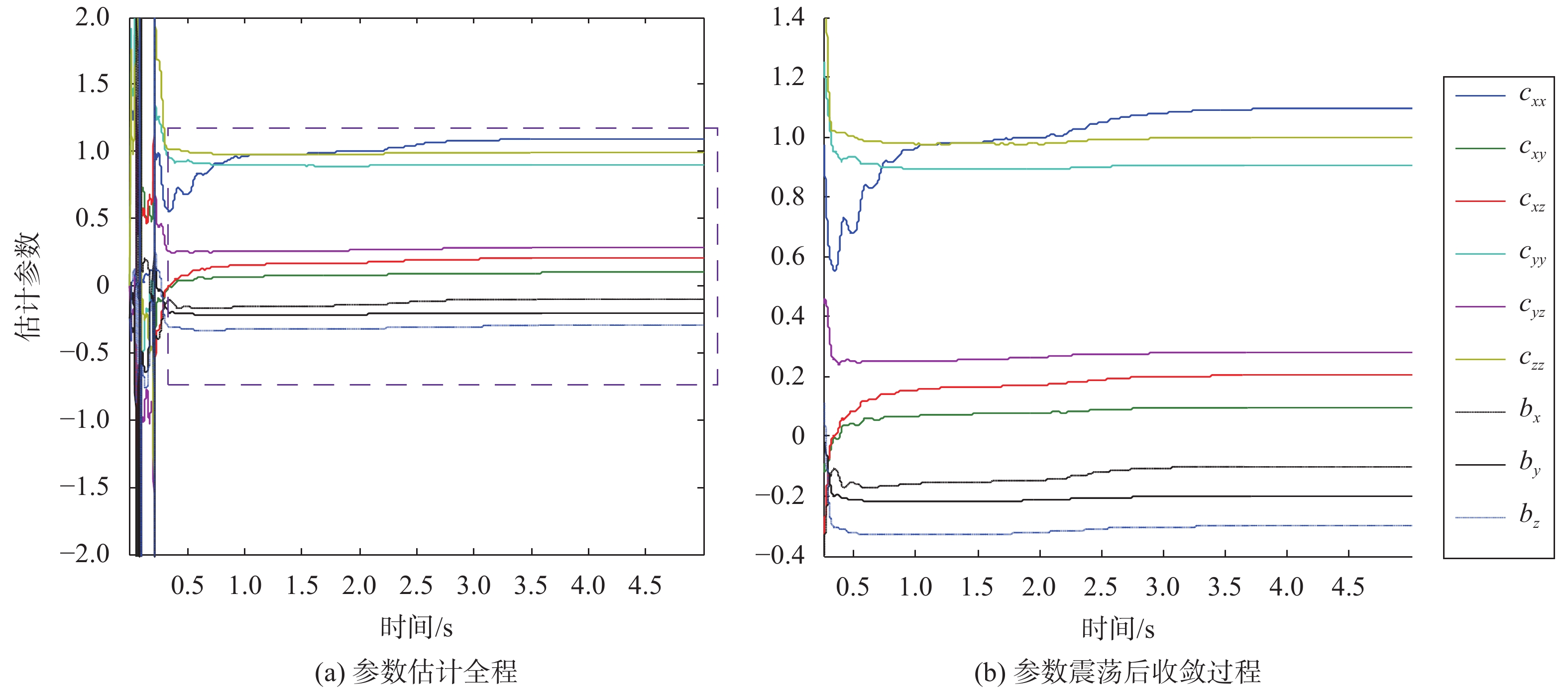
|
| 图 3 试验I中弹体固定磁场和感应磁场系数的估计过程 |
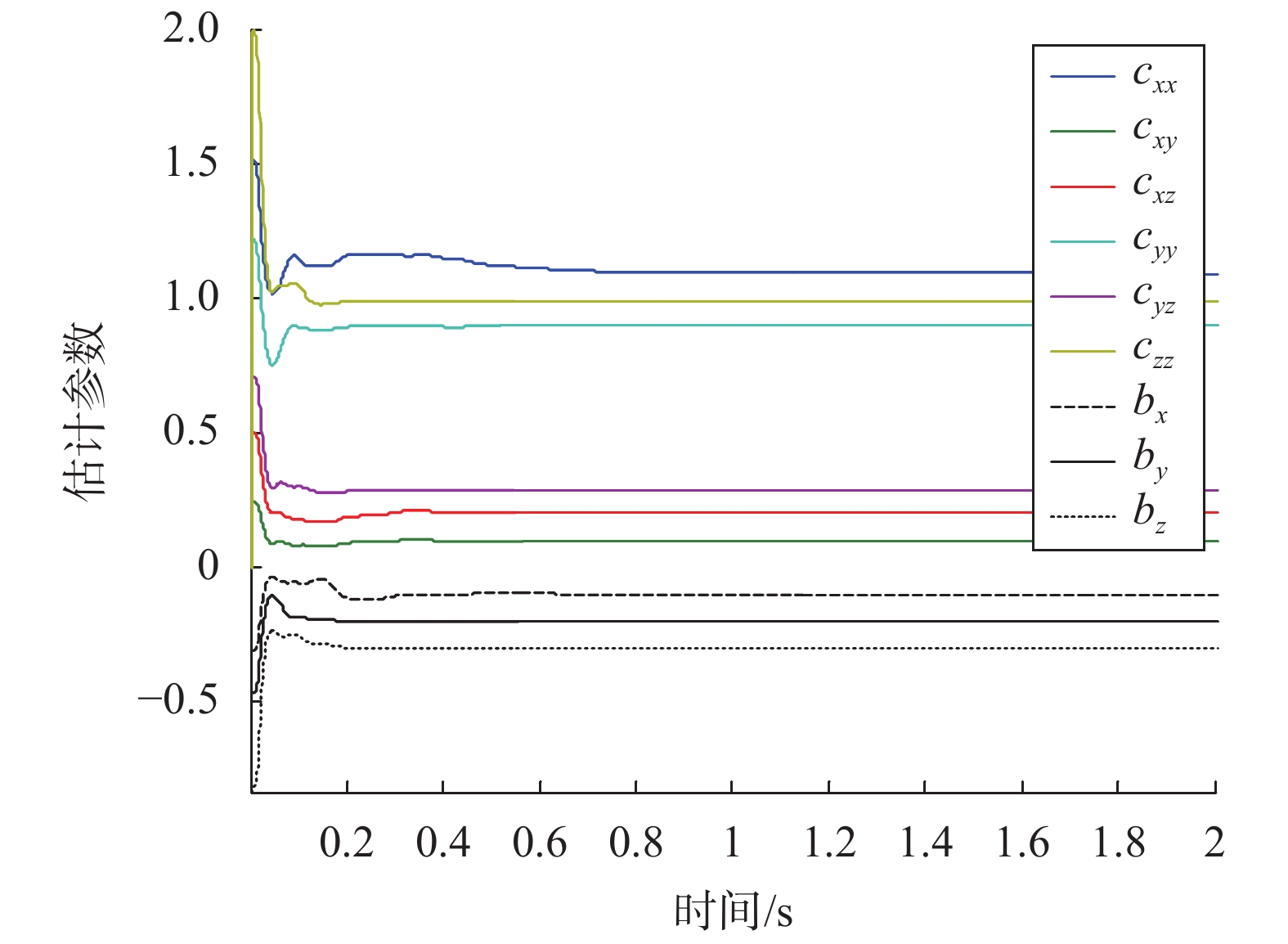
|
| 图 4 试验 II 中弹体固定磁场和感应磁场系数的估计过程 |
3.2 转台试验
为了进一步验证在线校正算法的补偿效果,使用如图5所示的飞行转台模拟弹体飞行过程的姿态变化,进行校正试验。试验转台设置为:转台内框以5 r/s的转速转动,中框由45°线性变化到–45°,外框静止,整个过程持续5 s。为了模拟弹载下的磁干扰环境,将系统装配在含有铁磁材料的弹体尾翼中,再通过圆筒形工装将系统固连到飞行转台的内框上。

|
| 图 5 转台试验 |
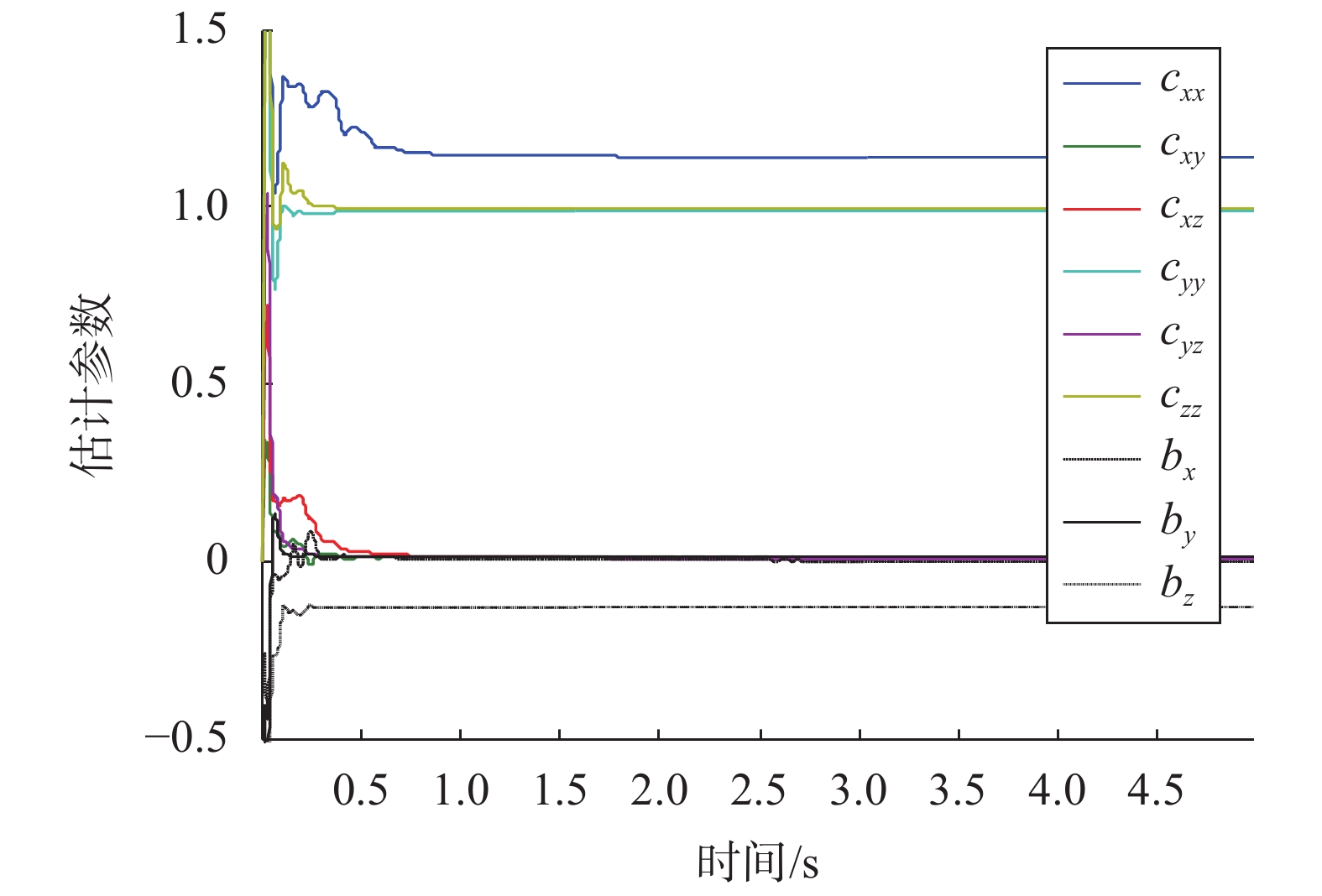
本次试验中,在线校正算法得到的弹体磁环境误差系数在线更新过程如图6所示,各系数最终收敛值如表2所示,磁测误差的补偿效果如图7所示。可以看出校正前x、y、z各轴的测量误差均值接近固定磁场误差系数,校正后的测量误差更接近测量噪声。采用12位置点记录滚转角数据,利用表1标定的误差系数对数据补偿,分别利用补偿前后的磁场数据进行滚转角解算,对比滚转角解算误差如图8所示。校正前滚转角解算误差达到了8°,残差均值为0.547°,标准差为5.59°;校正后滚转角解算精度优于1°,残差均值为–0.251°,标准差为0.367°。试验表明通过在线校正算法的补偿,可以满足高精度的磁场测量需求,验证了算法的有效性。

|
| 图 7 磁补偿误差(Gauss)对比图 |
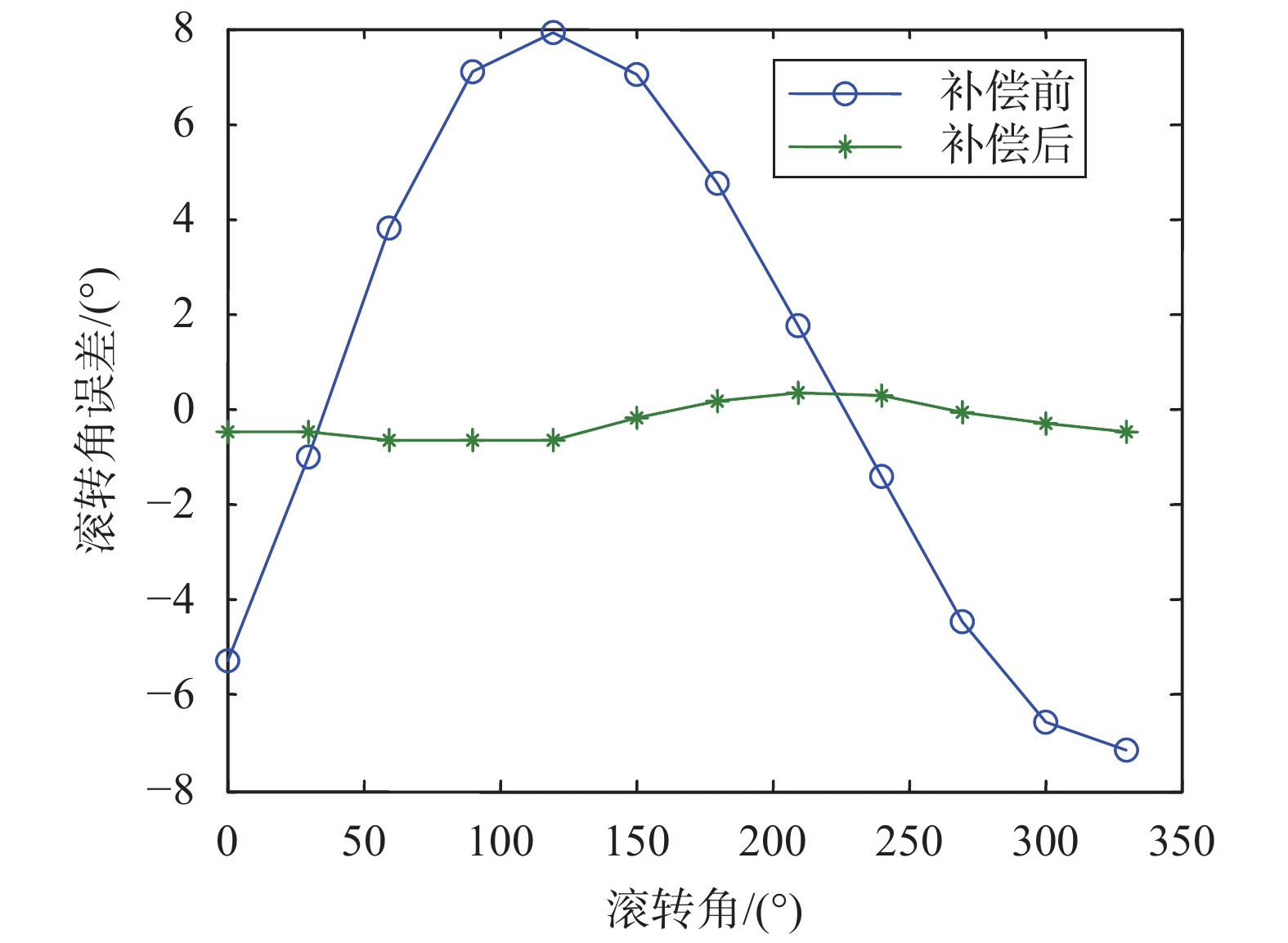
|
| 图 8 滚转角误差 |
|
| 图 6 转台中弹体固定磁场和感应磁场系数的更新过程 |
| bx | cxx | cxy | cxz |
| 0.001 2 | 1.135 9 | 0.008 3 | 0.010 5 |
| by | cyx | cyy | cyz |
| 0.015 04 | 0.008 3 | 0.988 4 | –0.004 8 |
| bz | czx | czy | czz |
| –0.132 6 | 0.010 5 | –0.004 8 | 0.993 2 |
4 结束语
本文提出了一种用于校正旋转弹捷联地磁传感器的在线算法。不同于传统的直接椭球拟合标定法和“二步校准法”,该算法使用线性模型实时校正磁测误差,能实现弹体层次化误差系数的在线更新,且计算量小。该算法根据磁传感器测量的误差模型,将固定磁场和感应磁场模型系数转换到椭球方程的参数上,再通过卡尔曼滤波算法估计方程参数,从而实现误差系数的在线更新。该算法提出了事先标定法建立初始条件,并经过了仿真试验和转台试验。试验结果表明,该在线算法具有非常好的估计精度,可有效补偿弹体磁场干扰误差,实现磁传感器的高精度测量。该算法具有适用性,不仅可以实现弹体磁场误差的校正,还实现磁传感器误差的校正。
| [1] |
陈国彬. 弹载三轴磁测系统设计与误差标定补偿技术研究[D]. 太原: 中北大学, 2012.
|
| [2] |
龙礼, 张合, 刘建敬. 地磁陀螺复合测姿系统误差补偿方法[J].
火力与指挥控制, 2014(7): 102-105.
DOI:10.3969/j.issn.1002-0640.2014.07.025 |
| [3] |
GEBRE E. A non-linear, two-step estimation algorithm for calibrating solid-state strapdown magnetometers[J].
International St Petersburg Conference on Navigation Systems, 2001, 28-30.
|
| [4] |
王婕, 郭子祺, 刘建英. 固定翼无人机航磁探测系统的磁补偿模型分析[J].
航空学报, 2016, 37(11): 3435-3443.
|
| [5] |
GOPAL B V, SARMA V N, RAMBABU H V. Real time compensation for aircraft induced noise during high resolution airborne magnetic surveys[J].
J Ind Geophys Union, 2004, 46: 48-52.
|
| [6] |
张晓明, 赵剡. 基于椭圆约束的新型载体磁场标定及补偿技术[J].
仪器仪表学报, 2009, 30(11): 2438-2443.
DOI:10.3321/j.issn:0254-3087.2009.11.035 |
| [7] |
赵鑫炉, 张晓明, 白渚铨, 等. 基于磁阻传感器的航姿测量系统罗差补偿技术研究[J].
传感技术学报, 2013(11): 1504-1507.
DOI:10.3969/j.issn.1004-1699.2013.11.007 |
| [8] |
Process for compensating the magnetic disturbances in the determination of a magnetic heading, and devices for carrying out this process: US 4414753 A[P].[2018-06-08]
|
| [9] |
郭鹏飞, 华春红, 任章, 等. 基于递推最小二乘的航姿系统罗差校正[J].
中国惯性技术学报, 2008, 16(1): 24-27.
|
| [10] |
孙宏伟, 房建成, 李艳. 椭圆拟合方法在磁罗盘罗差校准中的应用[J].
光学精密工程, 2009, 17(12): 3034-3039.
DOI:10.3321/j.issn:1004-924X.2009.12.024 |
| [11] |
韩兰懿, 米松林, 潘建军, 等. 一种无人机罗差修正方法[J].
航空计算技术, 2013, 43(3): 69-72.
DOI:10.3969/j.issn.1671-654X.2013.03.018 |
| [12] |
GEBREEG Z. Calibration of strapdown magnetometers in magnetic field domain[J].
Journal of Aerospace Engineering, 2014, 19(2): 87-102.
|
| [13] |
张晓明, 赵剡. 一种快速载体磁场补偿方法研究[J].
中北大学学报(自然科学版), 2009, 30(3): 286-291.
DOI:10.3969/j.issn.1673-3193.2009.03.018 |
| [14] |
GRANDVALLET B, ZEMOUCHE A, BOUTAYEB M, et al. Real-time attitude-independent three-axis magnetometer calibration for spinning projectiles: a sliding window approach[J].
IEEE Transactions on Control Systems Technology, 2013, 22(1): 255-264.
|
 2019, Vol. 45
2019, Vol. 45


 ,
,