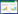文章信息
- 张晓明, 陈雷, 张莺莺, 檀杰, 朱孟龙
- ZHANG Xiaoming, CHEN Lei, ZHANG Yingying, TAN Jie, ZHU Menglong
- 基于EKF的地磁/陀螺信息融合姿态测量算法研究
- EKF attitude measurement algorithm based on geomagnetic/gyro information fusion
- 中国测试, 2019, 45(5): 10-16
- CHINA MEASUREMENT & TEST, 2019, 45(5): 10-16
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018100008
-
文章历史
- 收稿日期: 2018-10-07
- 收到修改稿日期: 2018-11-13
现代战争要求进攻武器具备精确打击能力和快速响应能力,传统的常规弹药无法满足这种要求,必须对常规弹药进行制导化改造,而改造的核心为弹体姿态的准确测量。由于受常规弹药高旋转、高冲击、小体积的应用环境限制,传统的弹载姿态测量方案中,单一使用磁传感器无法实现全姿态角的实时解算,并且其精度易受弹体俯仰方向变化和干扰磁场的影响[1-2]。而常规组合导航算法计算量大,数据更新率低,信息融合精度低,不能满足制导弹药的实时性、可靠性和精度要求[3-5]。因此需要一种高精度的信息融合姿态测试方案,以满足全姿态角高精度实时解算和适应复杂的弹载环境要求。
对于上述问题,文献[6]提出了由单轴陀螺和三轴地磁传感器组合姿态测量方案,利用单轴陀螺积分得到轴向滚转角,进而由滚转角结合地磁传感器信息解算得到俯仰角和偏航角;该解算虽然方法简单,但是滚转角初值不易获取,并且精度受到限制。文献[7]采用的方法由于基于实际弹道可以较好匹配模版弹道,从而获得一些飞行特征参数,在发射前将其装订供弹载飞行使用,发射后将弹道参数与三轴磁传感器信息结合从而解算姿态角,最后用一个扩展卡尔曼滤波器融合磁传感器和陀螺仪的信息,提高解算精度和系统稳定性;这种方法在实际弹道模型准确的情况下具有较高精度,但是其过程复杂,实际弹道与匹配弹道总有偏差,而无法获得较高的精度。文献[8]采用权系数和卡尔曼滤波算法对地磁/陀螺组合测姿中的仿真信号进行处理,得到较好的结果,证明其算法的适用性;但卡尔曼滤波算法是针对线性高斯的情况,仅用于线性系统处理。以上方案分别从传感器组合、弹道匹配、算法处理3个方面对信息融合姿态进行了测试,但均不能满足复杂弹载环境全姿态角实时解算要求。
本文提出一种基于EKF的地磁/陀螺信息融合姿态测量方法。利用三轴陀螺仪和三轴磁传感器对弹体姿态角进行解算,避免了精度受限的问题且滚转角易获取,利用EKF将非线性方程线性化,进而对仿真信号进行处理,避免了弹道匹配的偏差且可以处理非线性系统。
1 基于EKF的地磁/陀螺信息融合姿态测量算法设计 1.1 坐标系的定义及坐标系转换发射坐标系
|
| 图 1 坐标系的定义 |
弹体坐标系
为了得到弹体的姿态角,需要研究发射坐标系与载体坐标系之间的转换关系。载体坐标系固联在载体上,当弹体在飞行时载体坐标系也会发生变化,载体坐标系与发射坐标系之间的夹角就是弹体运动的姿态角[9]。设
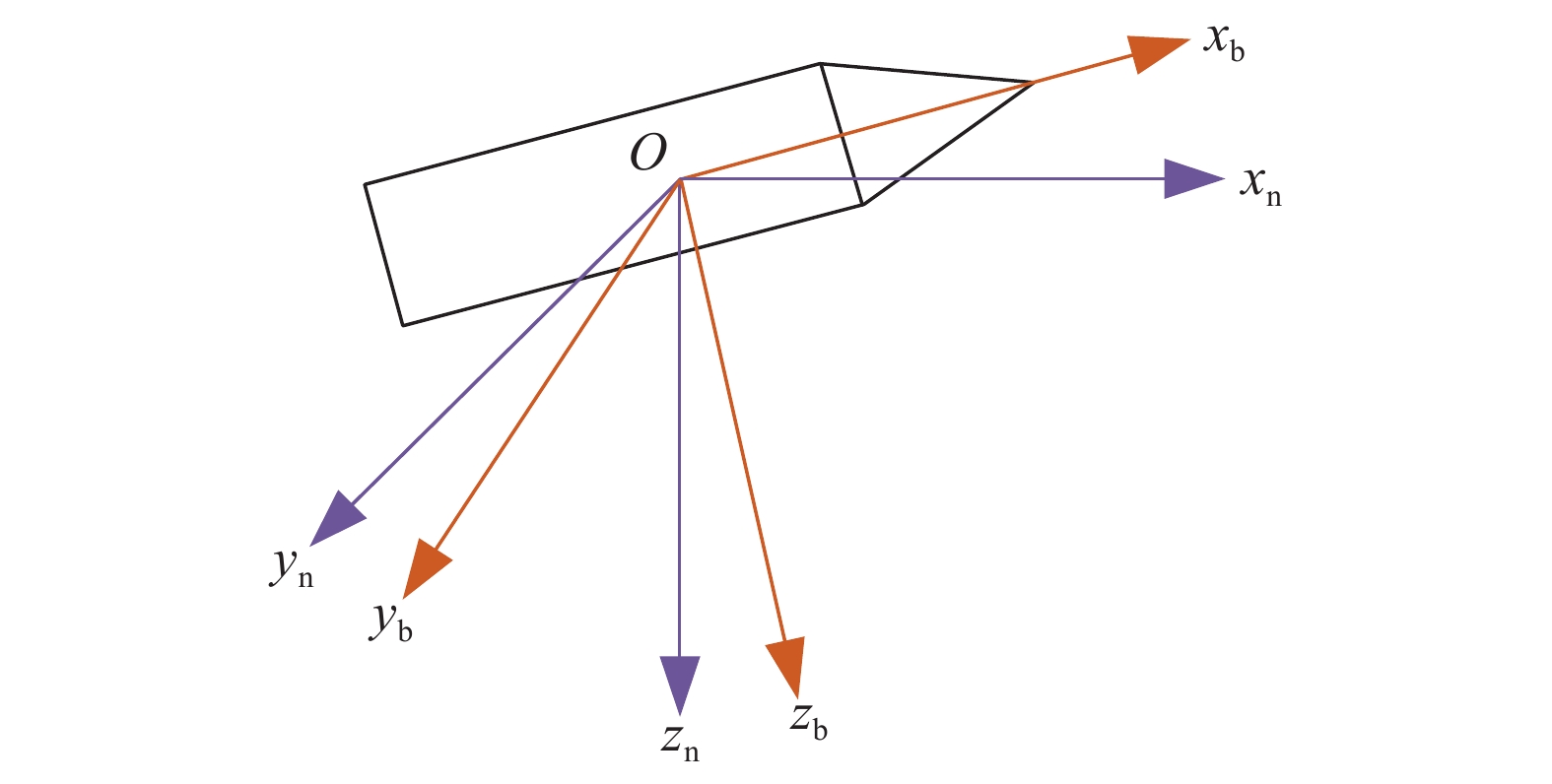
|
| 图 2 坐标系的转换 |
在图2中,发射坐标系经三次变化即可得到载体坐标系。在初始状态下,载体坐标系与发射坐标系完全重合。第一次转动后,发射坐标系
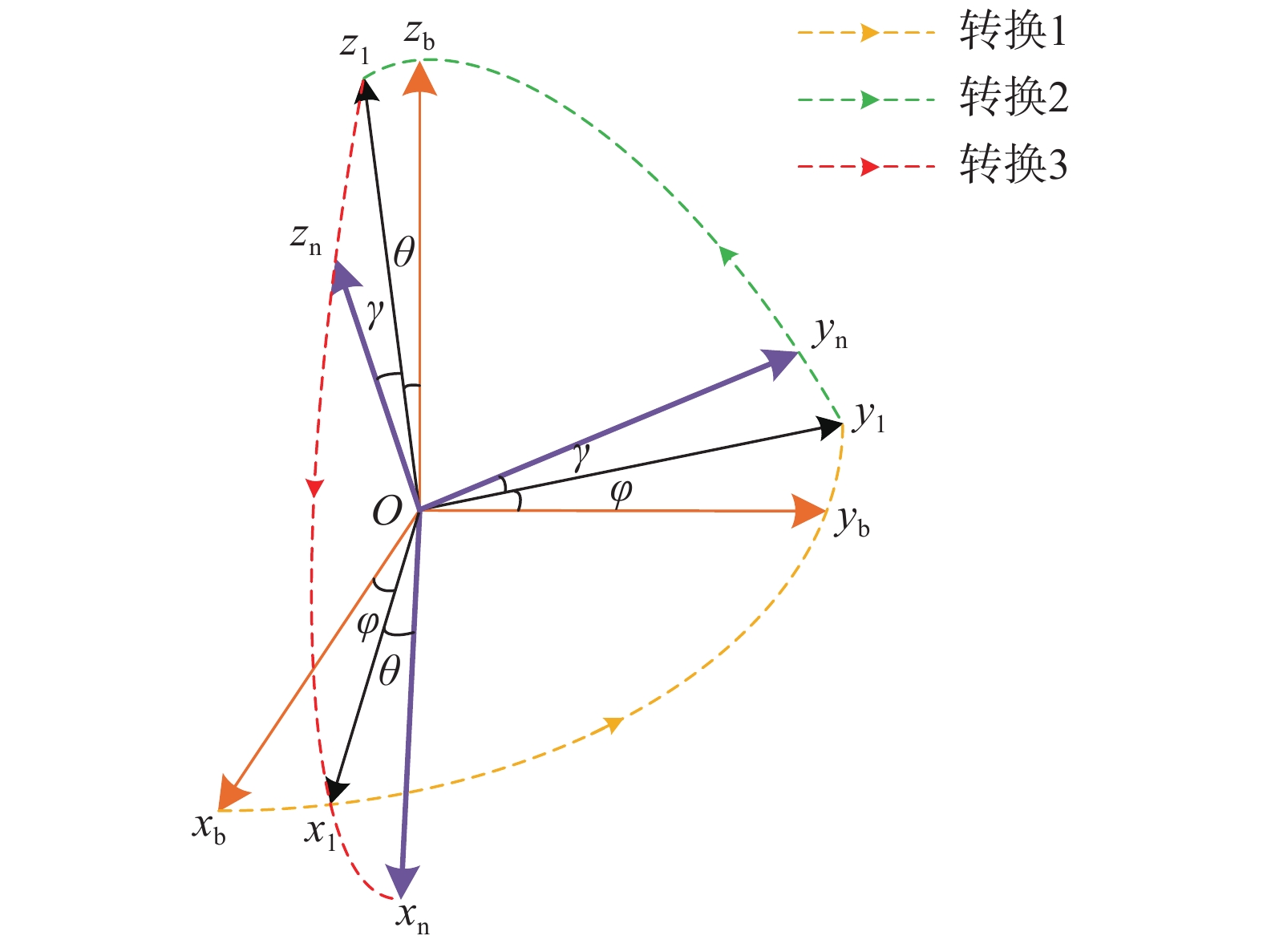
地磁/陀螺信息融合姿态测量原理如图3所示,其核心是设计一个扩展卡尔曼滤波器对姿态四元数进行估计,最终再由姿态四元数换算得到姿态角。首先依载体姿态角作为原始输入,由陀螺仪的测量可以得到载体坐标系相对发射坐标系的三轴角速率,再利用四元数微分方程得到姿态四元数信息。图3中的卡尔曼滤波器中,采用四元数微分方程作为状态方程,以姿态四元数为系统观测量,
|
| 图 3 地磁/陀螺信息融合姿态测量原理图 |
1.3 地磁/陀螺信息融合的扩展卡尔曼滤波器设计 1.3.1 基于四元数的地磁姿态测量原理
地磁传感器的测量值是地磁场在载体坐标系下的三分量
| ${{H}}_{\rm m}^{\rm b} = {{C}}_{\rm n}^{\rm b}{{H}}_{\rm e}^{\rm n}$ | (1) |
其中
| ${{C}}_{\rm n}^{\rm b}{{ = }}\left[ {\begin{array}{*{20}{c}} {\cos \varphi \cos \theta }&{\cos \theta \sin \varphi }&{ - \sin \theta } \\ {\cos \varphi \sin \theta \sin \gamma - \cos \gamma \sin \varphi }&{\cos \varphi \cos \gamma + \sin \gamma \sin \theta \sin \varphi }&{\cos \theta \sin \gamma } \\ {\sin \varphi \sin \gamma + \cos \varphi \sin \theta \cos \gamma }&{\cos \gamma \sin \varphi \sin \theta - \cos \varphi \sin \gamma }&{\cos \gamma \cos \theta } \end{array}} \right]$ | (2) |
由于转换矩阵
用四元数代替姿态角表示从地理坐标系到弹体坐标系的转换矩阵[11],有:
| $\left[ \begin{gathered} {H_x} \\ {H_y} \\ {H_z} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {q_0^2 + q_1^2 - q_2^2 + q_3^2}&{2({q_1}{q_2} + {q_0}{q_3})}&{2({q_1}{q_3} - {q_0}{q_2})} \\ {2({q_1}{q_2} - {q_0}{q_3})}&{q_0^2 - q_1^2 + q_2^2 - q_3^2}&{2({q_2}{q_3} + {q_0}{q_1})} \\ {2({q_1}{q_3} + {q_0}{q_2})}&{2({q_2}{q_3} - {q_0}{q_1})}&{q_0^2 - q_1^2 - q_2^2 + q_3^2} \end{array}} \right]\left[ \begin{gathered} H_x^{\rm n} \\ H_y^{\rm n} \\ H_{\textit z}^{\rm n} \end{gathered} \right]$ | (3) |
根据载体坐标系和发射坐标系的定义,可以得到描述角速率和角位置关系的四元数微分方程:
| $\left[ \begin{gathered} {{\dot q}_0} \\ {{\dot q}_1} \\ {{\dot q}_2} \\ {{\dot q}_3} \\ \end{gathered} \right] = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _x}}&{ - {\omega _y}}&{ - {\omega _{\textit z}}} \\ {{\omega _x}}&0&{{\omega _{\textit z}}}&{ - {\omega _y}} \\ {{\omega _y}}&{ - {\omega _{\textit z}}}&0&{{\omega _x}} \\ {{\omega _{\textit z}}}&{{\omega _y}}&{ - {\omega _x}}&0 \end{array}} \right]\left[ \begin{gathered} {q_0} \\ {q_1} \\ {q_2} \\ {q_3} \\ \end{gathered} \right]$ | (4) |
式(4)可以转化为:
| $\dot {{Q}} = \frac{1}{2}{{{M}}^ * }({ \omega} _{\rm nb}^{\rm b}){{Q}}$ | (5) |
取
| ${{Q}}({t_{k + 1}}) = {{\rm e}^{\frac{1}{2}\int_{{t_k}}^{{t_{k + 1}}} {{M^ * }} ({ \omega} _{\rm nb}^{\rm b}){\rm d}t}}{{Q}}({t_k})$ | (6) |
将其离散化,假设一个周期内的陀螺仪的角速度为一固定值,令:
| $\Delta {{\Theta }}\left( k \right) = \int_{{t_k}}^{{t_{k + 1}}} {{{{M}}^ * }({ \omega} _{\rm nb}^{\rm b}){\rm d}t} \approx \left[ {\begin{array}{*{20}{c}} 0&{ - \Delta {\theta _x}}&{ - \Delta {\theta _y}}&{ - \Delta {\theta _{\textit z}}} \\ {\Delta {\theta _x}}&0&{\Delta {\theta _{\textit z}}}&{ - \Delta {\theta _y}} \\ {\Delta {\theta _y}}&{ - \Delta {\theta _{\textit z}}}&0&{\Delta {\theta _x}} \\ {\Delta {\theta _{\textit z}}}&{\Delta {\theta _y}}&{ - \Delta {\theta _x}}&0 \end{array}} \right]$ | (7) |
则得到四元数离散化的齐次线性方程解为:
| ${{{Q}}_{k + 1}} = {{\rm e}^{\frac{1}{2}\Delta {\Theta} \left( k \right)}}{{{Q}}_k}$ | (8) |
已知载体初始四元数和任何时刻下陀螺仪的输出角速度数据,就能求得更新后的四元数。
1.3.3 EKF状态方程和观测方程的建立以姿态四元数Q为状态量,建立如下的状态方程为:
| ${{x}}\left( {k + 1} \right) = {{\rm e}^{\frac{1}{2}\Delta {{\Theta }}\left( k \right)}}{{x}}\left( k \right) + {{v}}\left( k \right)$ | (9) |
其中
| ${\rm E}\left\{ {{{\nu }}(k){{{\nu }}^{\rm T}}(k)} \right\} = {{M}}$ | (10) |
以式(3)所示的磁传感器四元数姿态测量模型建立观测方程。因为式(3)是非线性,因此建立非线性系统观测方程为:
| ${{y}}(k) = {{{g}}_k}({{x}}(k)) + {{n}}(k)$ | (11) |
其中:
| $ {{{g}}_k}({{x}}(k)) = \left[ {\begin{aligned} &{H_x^{\rm n}(q_0^2 + q_1^2 - q_2^2 + q_3^2) + 2H_y^{\rm n}({q_1}{q_2} + {q_0}{q_3}) + 2H_{\textit z}^{\rm n}({q_1}{q_3} - {q_0}{q_2})} \\ & {2H_x^{\rm n}({q_1}{q_2} - {q_0}{q_3}) + H_y^{\rm n}(q_0^2 - q_1^2 + q_2^2 - q_3^2) + 2H_{\textit z}^{\rm n}({q_2}{q_3} + {q_0}{q_1})} \\ & {2H_x^{\rm n}({q_1}{q_3} + {q_0}{q_2}) + 2H_y^{\rm n}({q_2}{q_3} - {q_0}{q_1}) + H_{\textit z}^{\rm n}(q_0^2 - q_1^2 - q_2^2 + q_3^2)} \end{aligned}} \right]$ | (12) |
| ${\rm E}\left\{ {{{n}}(k){{{n}}^{\rm T}}(k)} \right\} = {{N}}$ | (13) |
从而得到如下形式的非线性系统模型为:
| $\left\{ \begin{aligned} &{{x}}\left( k \right) = {{\rm e}^{\frac{1}{2}\Delta {{\Theta }}\left( k \right)}}{{x}}\left( k \right) + {{v}}\left( k \right) \\ &{{y}}(k) = {{{g}}_k}({{x}}(k)) + {{n}}(k) \\ \end{aligned} \right.$ | (14) |
其中
| ${{\hat x}}\left( {k + 1|k} \right) = {{\rm e}^{\frac{1}{2}\Delta {{\Theta }}\left( k \right)}}{{x}}\left( k \right)$ | (15) |
协方差的更新需要每步都计算Jacobian矩阵,进一步计算Jacobian矩阵:
| ${{F}}\left( k \right) = {{\rm e}^{\frac{1}{2}\Delta {{\Theta }}\left( k \right)}}$ | (16) |
| ${{G}}\left( {k + 1} \right) = \frac{{\partial {{{g}}_k}\left( x \right)}}{{\partial {{x}}}}\left| {_{{{x}} = {{\hat x}}\left( {k + 1\left| k \right.} \right)}} \right.$ | (17) |
随后,协方差矩阵
| ${{{P}}^ - }\left( {k + 1} \right) = {{F}}\left( k \right){{P}}\left( k \right){{{F}}^{\rm T}}\left( k \right) + {{M}}\left( k \right)$ | (18) |
| $ \begin{split} { K}\left( {k + 1} \right) =& {{{P}}^ - }\left( {k + 1} \right){{G}}\left( {k + 1} \right){\left[ {{{G}}\left( {k + 1} \right){{{P}}^ - }\left( {k + 1} \right)}\right.} \\ &\left.{{{G}}^{\rm T}}\left( {k + 1} \right) + {{N}}\left( {k + 1} \right) \right]^{ - 1}\end{split}$ | (19) |
| ${{P}}\left( {k + 1} \right) = \left[ {{{I}} - {{K}}\left( {k + 1} \right){{G}}\left( {k + 1} \right)} \right]{{{P}}^ - }\left( {k + 1} \right)$ | (20) |
状态估计是利用真实非线性关系进行校正的,写成:
| $ \begin{split} {{\hat x}}\left( {k + 1|k + 1} \right) =& {{\hat x}}\left( {k + 1|k} \right) + {{K}}\left( {k + 1} \right)\left[ {{{y}}\left( {k + 1} \right)} -\right. \\& \left.{{{g}}_{k + 1}}\left( {{{\hat x}}\left( {k + 1|k} \right)} \right)\right] \end{split}$ | (21) |
根据式(21),最后得出状态四元数估计值,根据四元数与姿态转换矩阵的关系求得载体的姿态角为:
| $\left\{ \begin{aligned} &\varphi = \arctan \frac{{2({q_0}{q_1} + {q_2}{q_3})}}{{{q_0}^2 - {q_1}^2 - {q_2}^2 + {q_3}^2}} \\ &\theta = \arcsin [2({q_0}{q_2} - {q_1}{q_3})] \\ &\gamma = \arctan \frac{{2({q_0}{q_3} + {q_1}{q_2})}}{{{q_0}^2 + {q_1}^2 - {q_2}^2 - {q_3}^2}} \\ \end{aligned} \right.$ | (22) |
依据弹道质心运动学方程和弹丸绕质心转动的运动学方程,由于质心运动分析可以忽略其他星球对制导弹的影响,导弹仅仅受到地球引力作用,不考虑地球自转及其绕太阳的公转,并且认为地球为一个质量分布均匀的圆球体,因此导弹轨迹可以简化,不影响炮弹运动要求的精度[13]。设定初始条件,t=0时,弹丸初速v0=870 m/s,弹道初始倾角
| $\left\{ \begin{aligned} &\varphi = - \arctan \frac{{{v_{\textit z}}}}{{{v_x}}} \\ &\theta = \arctan \frac{{{v_y}}}{{\sqrt {v_x^2 + v_{\textit z}^2} }} \\ \end{aligned} \right.$ | (23) |
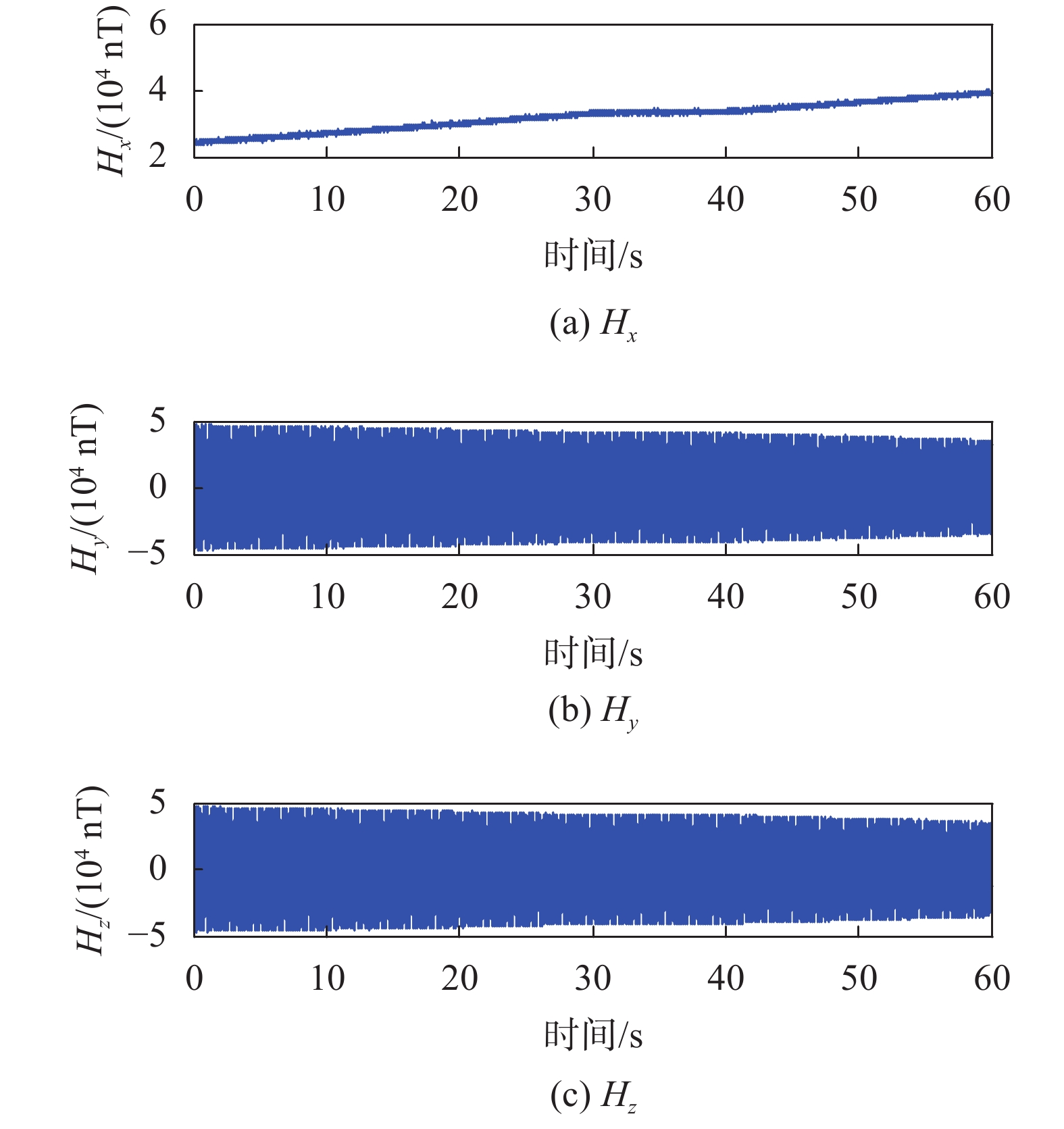
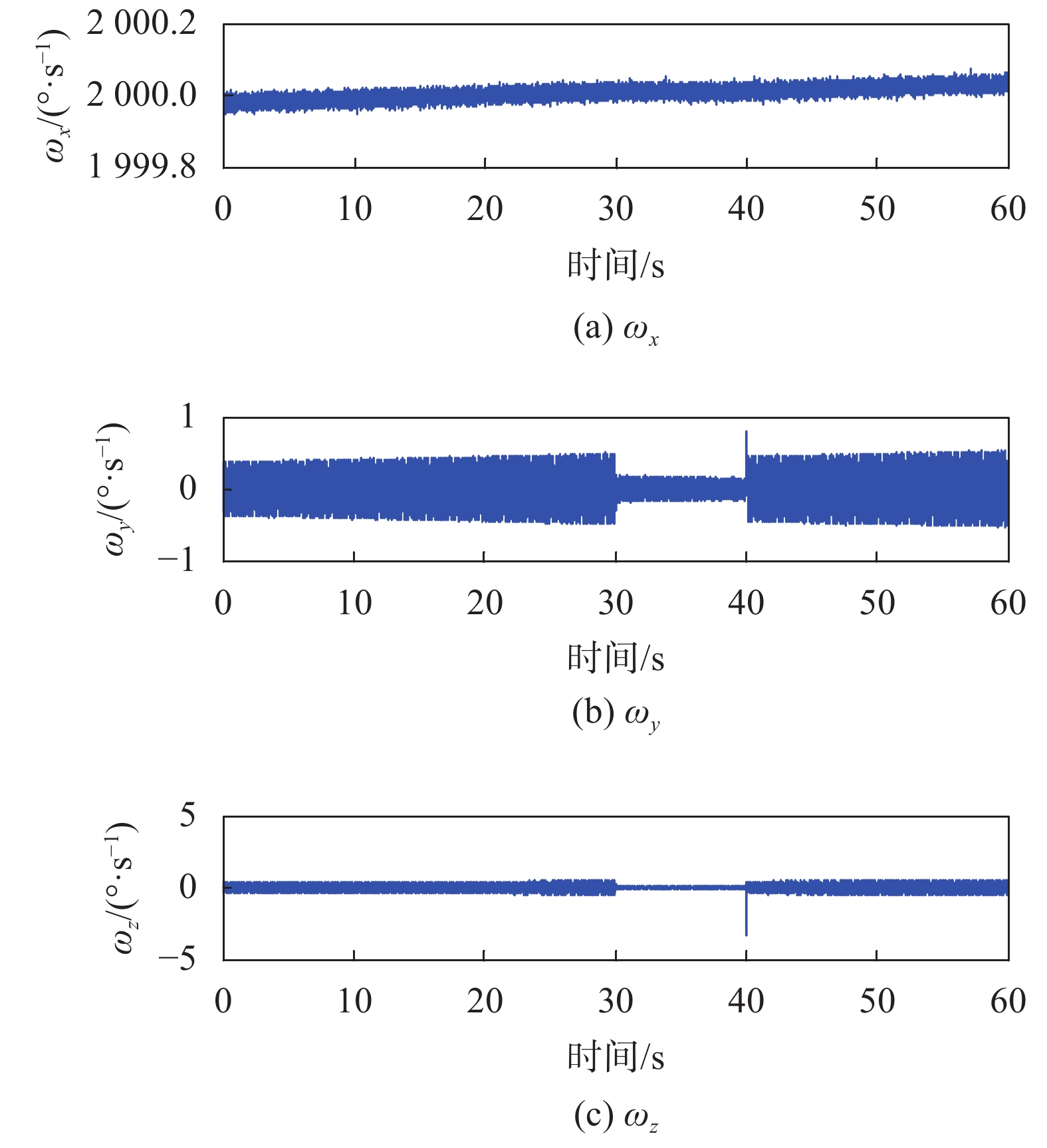
此外弹体轴向变化根据实际某型号弹设定参数,将其积分得到滚转角的姿态信息。理想姿态角的变化曲线如图4所示,由姿态角生成的仿真三轴磁场值和三轴陀螺如图5和图6所示。

|
| 图 4 理论姿态角曲线 |
|
| 图 5 三轴磁场仿真曲线 |
|
| 图 6 三轴陀螺仿真曲线 |
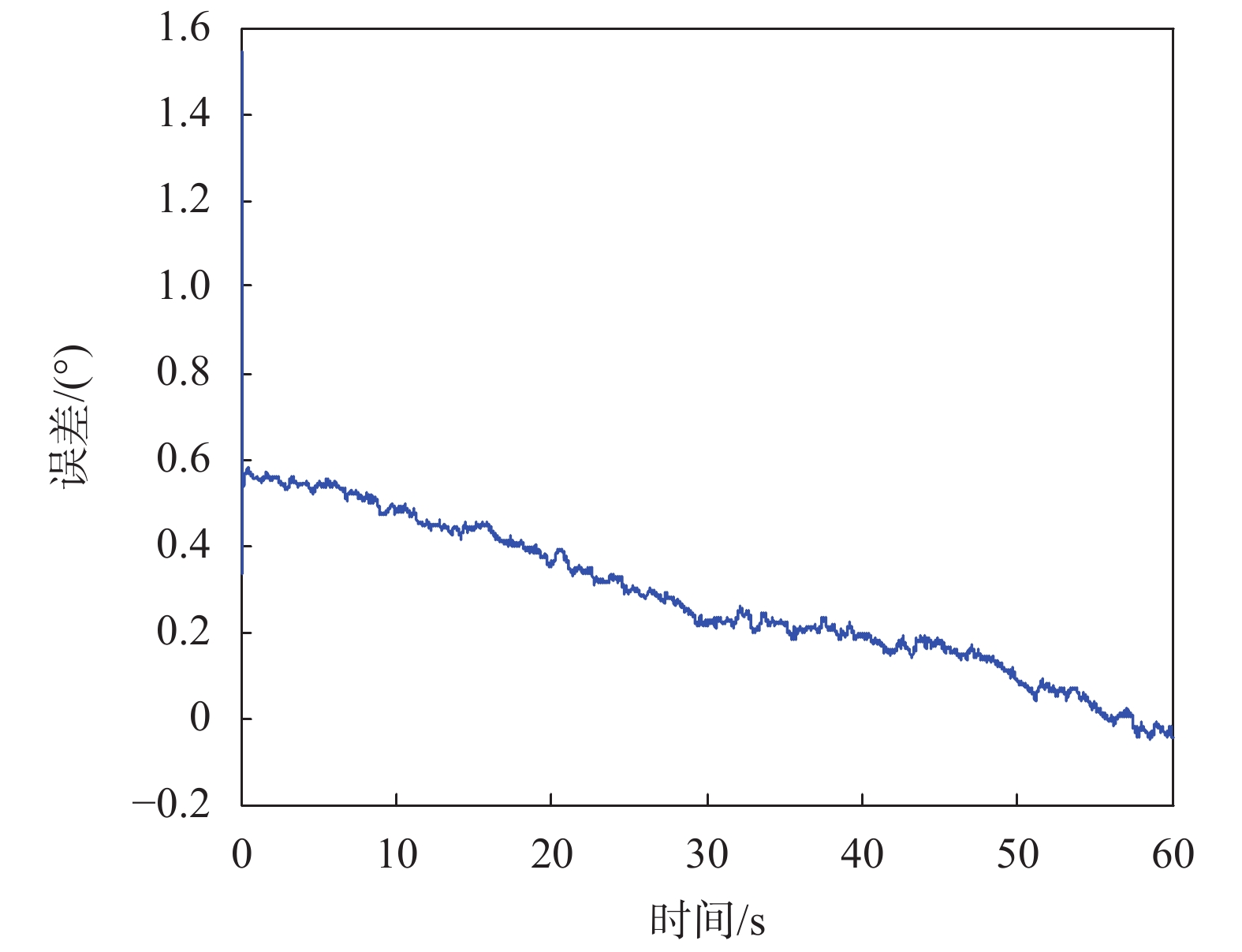
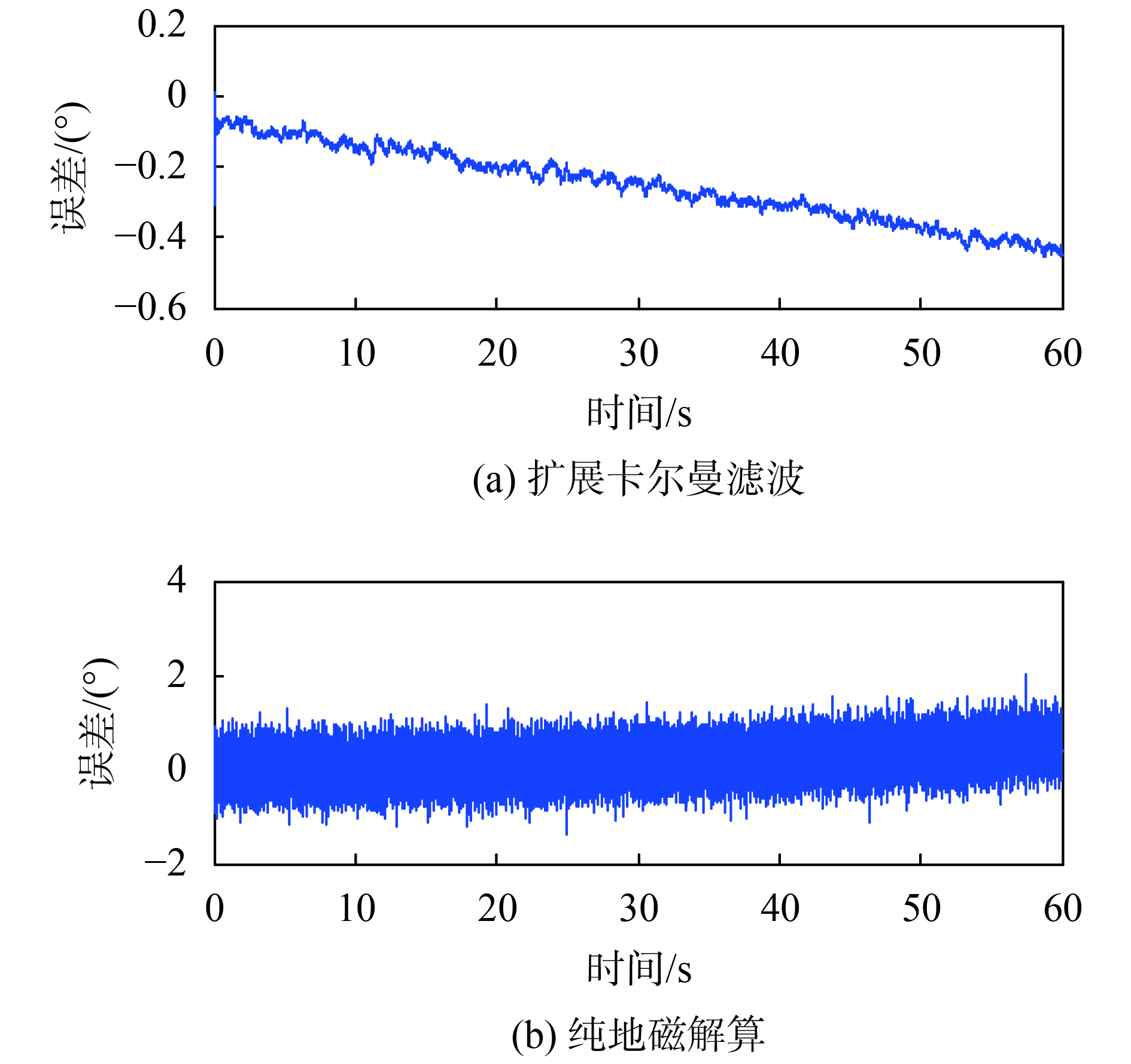
根据生成的三轴磁场信息和三轴陀螺信息运用EKF融合算法对其信息融合进行偏航角、俯仰角、滚转角的计算,并且与地磁解算的俯仰角和滚转角对比,得到如图7~图9所示误差曲线。
|
| 图 7 融合算法解算偏航角误差曲线 |
|
| 图 8 仿真试验俯仰角误差曲线 |
|
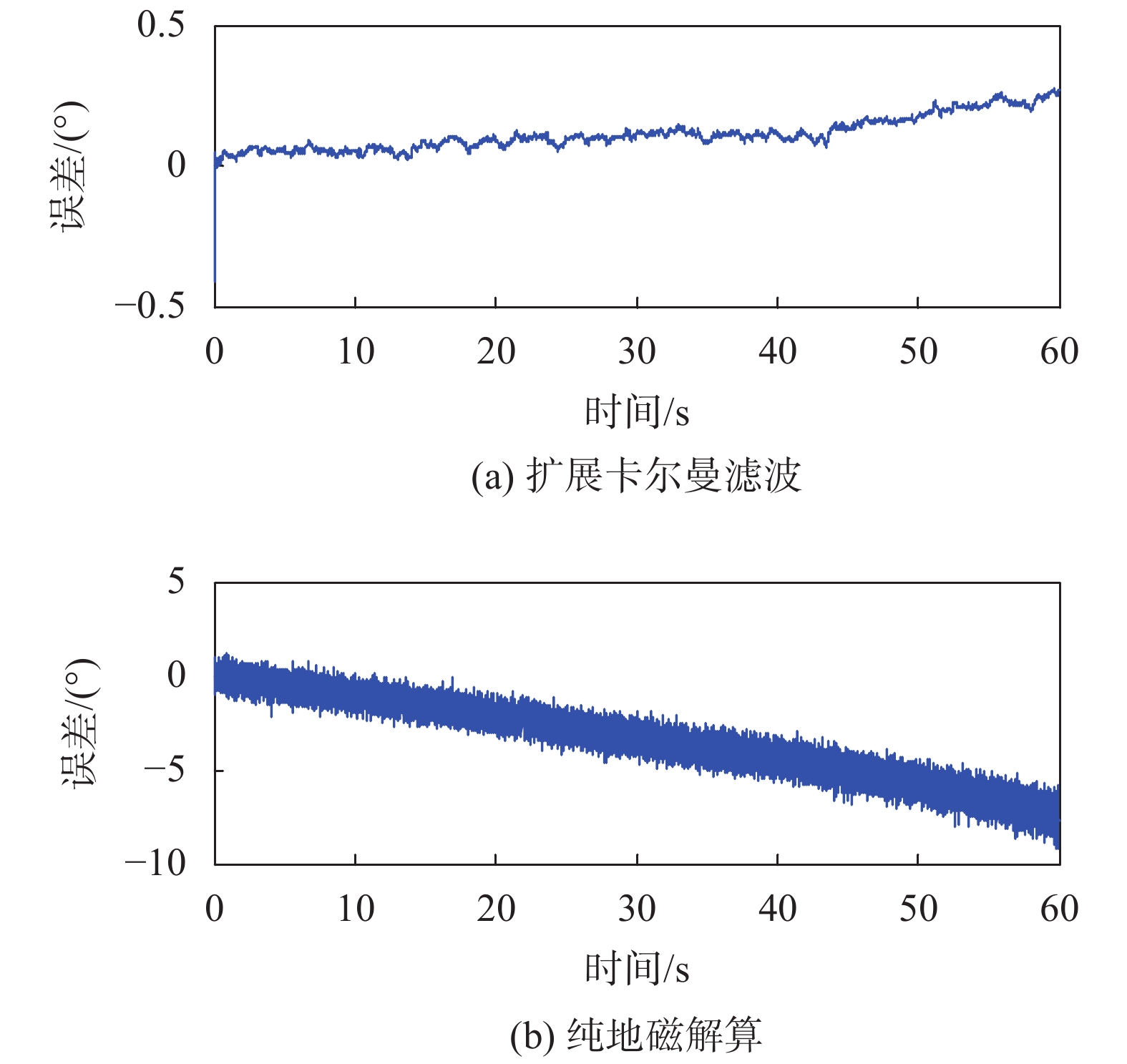
| 图 9 仿真试验滚转角误差曲线 |
根据图7~图9对于导弹飞行模型仿真结果显示,制导弹飞行60 s落地,全程导弹轴向正转,无反转。对比EKF融合算法和纯地磁解算算法,EKF解算滚转角的误差均值为0.113 3°,标准差为0.058 5°,而纯地磁解算滚转角的误差标准差为−3.377 6°,标准差为2.129 5°;所以EKF融合算法的滚转角解算精度提高一个数量级以上,此外纯地磁解算滚转角误差最大为−9.158°,而EKF算法的滚转角误差在最后阶段最大仅为0.267 1°,滚转角解算精度较高。此外EKF解算俯仰角的误差均值为−0.253 6°,标准差为0.104 2°,纯地磁解算俯仰角的误差均值为0.174 4°,标准差为0.365 2°,所以EKF融合算法的噪声水平降低约1/3,在57.5 s地磁解算俯仰角误差最大达到2.013°,而EKF解算俯仰角误差均不超过−0.6°。纯地磁无法解算偏航角,而EKF解算偏航角的误差均值为0.276 7°,标准差为0.171 7°,全程最大不超过1°,解算偏航角精度较高。此融合算法不仅可以解算弹载3个姿态角,弥补了地磁传感器滚转角、俯仰角测量受偏航影响的缺陷,而且解算得到的姿态角均具有较高的精度和较低的噪声水平。
2.2 半物理试验验证把集成了HMC1043地磁传感器、ITG-3701陀螺仪(两个传感器的测量精度均在1 mV以内)的系统捷联安装于转台上(见图10),在转台的零点位置上(内框、中框、外框均为转台零位)预先装载地磁场初始三分量,上电内框在1 s内加速到5 r/s,外框在1 s内转动到30°,之后内框以5 r/s的速度转动,中框和外框均按照

|
| 图 10 飞行仿真转台试验 |
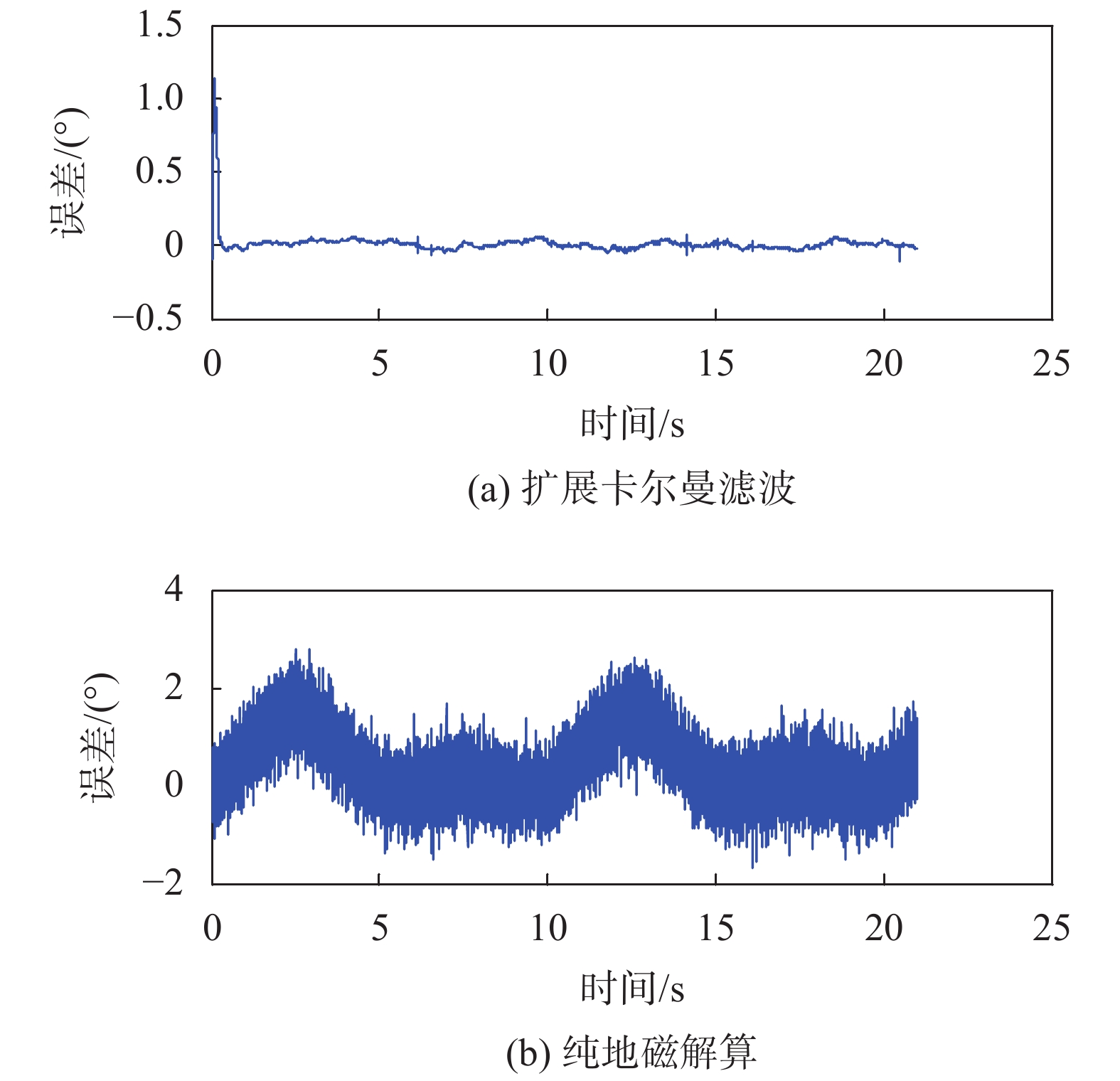
|
| 图 11 半物理试验滚转角误差曲线 |
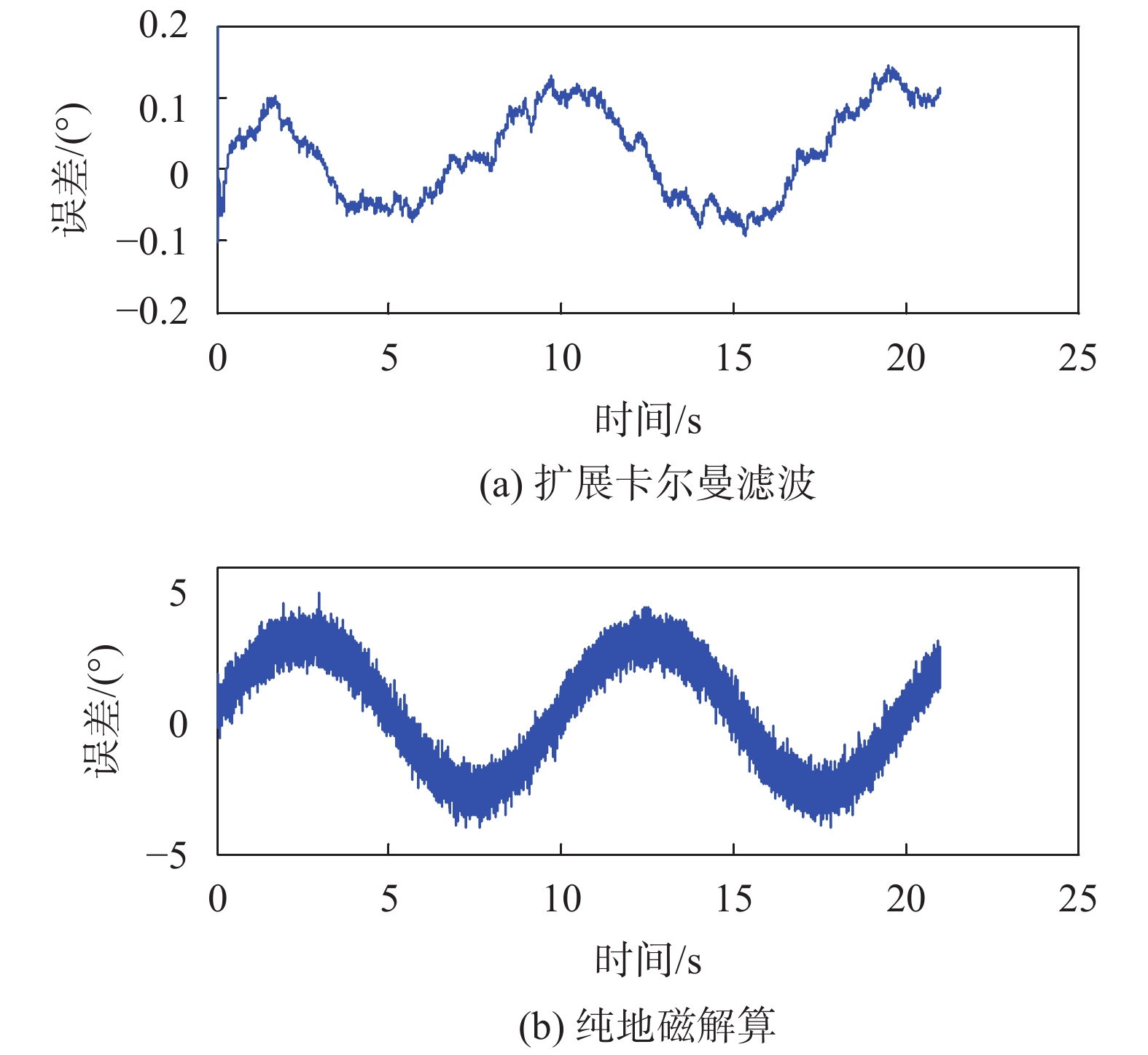
|
| 图 12 半物理试验俯仰角误差曲线 |
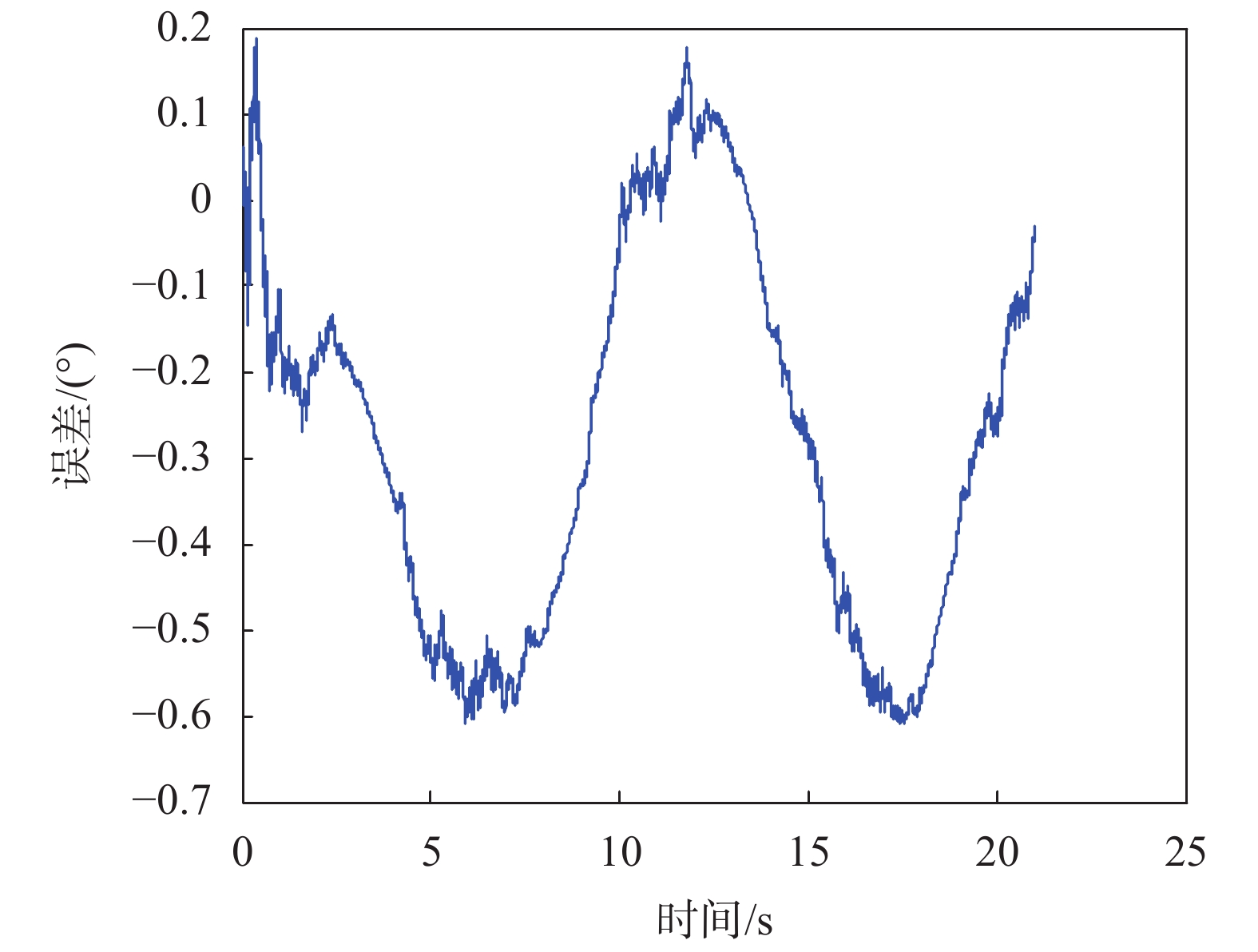
|
| 图 13 半物理试验偏航角误差曲线 |
由图11可以看出,EKF解算滚转角相比于纯地磁解算滚转角,精度得到明显改善,抗偏航和俯仰扰动能力提升,机动性较好。具体比较数据如表1所示。
由表1可得,EKF解算滚转角相比于纯地磁解算滚转角精度提高一个数量级以上,且标准差也减小为原来的1/10左右,噪声水平提高近一个数量级。
此外,由图12可以得出纯地磁解算俯仰角和EFK解算俯仰角均值相差不多,但从标准差和最大偏差来看,融合算法的俯仰角精度提高一个数量级以上,如表2所示。
从图13可以得出,EKF解算偏航角的误差均值为0.280 7°,标准差为0.222 8°,误差均在1°以内,进一步证明了EKF对于偏航角解算的准确度,可以融合地磁和陀螺信息实现全姿态角高精度解算。
3 结束语本文提出一种基于EKF的简单、高效、实时性、自适应的地磁/陀螺信息融合姿态测量方法。得到主要结论为:1)方法解算精度比地磁解算的滚转角和俯仰角提高一个数量级以上,而偏航角的解算误差在1°以内;2)采用信息融合后,外界干扰和全姿态机动的情况对解算精度影响较小,且解算姿态角误差较为稳定,变化幅度更小。
| [1] |
赵鑫炉. 基于MARG传感器的车辆姿态测量系统设计[D]. 太原:中北大学, 2014.
|
| [2] |
韩艳. 制导炮弹飞行姿态的陀螺/磁阻传感器组合测量方法研究[D]. 南京: 南京理工大学, 2010.
|
| [3] |
鲍亚琪, 陈国光, 吴坤, 等. 基于磁强计和MEMS陀螺的弹箭全姿态探测[J].
兵工学报, 2008, 29(10): 1227-1231.
DOI:10.3321/j.issn:1000-1093.2008.10.015 |
| [4] |
赵鑫炉, 张晓明, 龙达峰, 等. 旋转弹用滚转角磁测系统设计[J].
传感技术学报, 2013, 26(9): 1309-1313.
DOI:10.3969/j.issn.1004-1699.2013.09.025 |
| [5] |
龙达峰, 刘俊, 张晓明, 等. 高速旋转弹载体干扰磁场补偿算法[J].
弹箭与制导学报, 2016, 36(2): 151-156.
|
| [6] |
曹红松, 冯顺山, 赵捍东, 等. 地磁陀螺组合弹药姿态探测技术研究[J].
弹箭与制导学报, 2006, 26(3): 142-145.
DOI:10.3969/j.issn.1673-9728.2006.03.047 |
| [7] |
王嘉雨. 地磁/陀螺信息融合的姿态解算算法研究[D]. 太原: 中北大学, 2015
|
| [8] |
马秀丽. 基于磁阻/陀螺组合测量弹体飞行姿态的数据融合方法研究[D]. 南京: 南京理工大学, 2012.
|
| [9] |
代刚, 李枚, 苏伟, 等. 自旋导弹捷联式陀螺/地磁姿态测量方法[J].
中国惯性技术学报, 2010, 18(6): 702-705.
|
| [10] |
刘凯, 梁晓庚. 基于陀螺仪和磁强计的姿态解算方法研究[J].
计算机仿真, 2014(5): 39-41.
DOI:10.3969/j.issn.1006-9348.2014.05.010 |
| [11] |
赵鑫炉, 张晓明, 白渚铨, 等. 基于磁阻传感器的航姿测量系统罗差补偿技术研究[J].
传感技术学报, 2013(11): 1504-1507.
DOI:10.3969/j.issn.1004-1699.2013.11.007 |
| [12] |
GRANDVALLET B, ZEMOUCHE A, BOUTAYEB M, et al. Real-time attitude-independent three-axis magnetometer calibration for spinning projectiles: A sliding window approach[J].
IEEE Transactions on Control Systems Technology, 2013, 22(1): 255-264.
|
| [13] |
JULIER S J,UHLMANN J K ,DURRANT - WHYTE H F. A new method of the nonlinear transformation of means and covariance in filters and estimation[J].
IEEE Transactions on Automatic Control, 2000, 45(3): 477-428.
DOI:10.1109/9.847726 |
 2019, Vol. 45
2019, Vol. 45