0 引　言

模拟电路故障诊断是电子设备有效性验证的重要问题^[1-2]，模拟电路故障诊断方法依据仿真进行的时间划分为测前仿真方法和测后仿真方法^[3-4]。参数故障诊断通常采用测后仿真方法，通过求解测试方程得到待测元件的参数值，与标称值比对进行故障隔离定位。参数辨识法分为伴随网络法和多频诊断法^[5-6]。伴随网络法是根据Tellegen定理计算得到测点处各元件的灵敏度值，采用牛顿迭代方法和区间法等求解被测电路构成的多元非线性方程组，该方法计算量大。多频诊断法是指通过增加测试频率，得到更多的故障方程数，据此来确定元件值，该方法收敛效果差。近几年来参数辨识法取得了新的进展，He等^[7]将L1最优范数引入到非线性电路的参数估计，采用神经网络方法求解；Guo和Savir^[8]采用自回归模型和系统辨识工具进行模拟电路故障参数辨识；LONG等^[9]采用改进的灵敏度计算方法进行模拟电路的故障参数辨识。

对于复杂线性电路或非线性电路，电路代数方程很难求取或不存在、求解效率低等问题仍然存在，困扰着参数辨识方法的进一步发展。此外，由于元件容差影响，存在故障掩盖现象。同时，考虑方程的非线性，测试方程可能存在多解情况。综上分析，有必要寻求新技术途径来实现对模拟电路的故障参数辨识，本文针对容差条件下模拟电路的多软故障诊断问题开展研究，提出一种基于系统搜索的故障诊断和参数辨识方法。

1 算法原理

假设某被测电路中可能存在 $n$ 个参数故障，给该被测电路施加激励信号，同时在 $r$ 个测点处测量输出电压。对于 $m$ 个激励电压信号集合，测量得到 $mr$ 个输出电压，其中 $mr \geqslant n$ 。从中选取 $n$ 个测量电压，作为输出电压向量 ${{u}} = {[{u_1}, \cdots, {u_n}]^{\rm{T}}}$ 的元素，每个测量电压 ${u_i}$ 是电路可能故障参数 ${x_1}, \cdots ,{x_n}$ 的函数，表示为 ${u_i} = {{\hat f}_i}({ x}),i = 1,\cdots,n$ ，其中 ${{x}} = {[{x_1}, \cdots, {x_n}]^{\rm{T}}}$ 。得到的测试方程为

式中： $ {{f}}({{x}}) = {\hat{ f}}({{x}}) - {{u}}$ ；

$ {\hat{ f}}({{x}}) = {[{{\hat f}_1}({{x}}), \cdots, {{\hat f}_n}({{x}})]^{\rm{T}}}\text{。}$

实际电路中，往往无法得到非线性函数 ${\hat{ f}}({{x}})$ 的准确数学表达式，同时由于可用测点和激励点有限，测试方程中包含的信息往往不足以找到实际的故障参数集合，在数学上意味着式（1）包含多个解，因此需要找到一种能得到测试方程多解的方法。参照文献[10]，将代数问题转化为差分方程求解是一种有效寻找多解的方法。Chao等^[11]将该思想拓展为寻找非线性电阻电路多直流工作点的系统搜索方法。本文进一步将系统搜索的概念拓展应用于模拟电路故障诊断过程中测试方程的多解求解。

为了找到式（1）的多个解，将该问题转化为初值问题。设计差分方程为

由式（2）得到：

初值条件 ${{x}}(0)$ 的选择满足如下条件： ${f_i}({{x}}(0)) = 0$ ， $i = 1,\cdots,n - 1$ ，即 ${{x}}(0)$ 位于空间曲线 $l$ 上，该空间曲线为曲面 ${f_i}({{x}}) = 0$ ， $i = 1,\cdots,n - 1$ 的交叉部分。解式（3）中前 $n - 1$ 个方程得到：对于任意 ${{x}}(0) \in l$ ，跟踪点 ${{x}}(t)$ 保留在曲线 $l$ 上。初值问题式（3）的解 ${{x}}(t)$ 能够通过数值积分方法得到。任何位于曲线 $l$ 上的点 ${{x}}({t_k})$ ，满足 ${f_n}({{x}}({t_k})) = 0$ 都是式（1）的解。

由于 ${\rm d}{{f}}/{\rm d}t = ({\rm d}{{f}}/{\rm d}{{x}})({\rm d}{{x}}/{\rm d}t)$ ，式（2）在 ${{x}}$ 空间具有如下形式：

式中： ${{J}}({{x}}) = {\rm d}{{f}}/{\rm d}{{x}}$ 是 ${{f}}({{x}})$ 的雅克比矩阵；

$ {{w}}({{x}}) = {[ - {f_1}({ x}), \cdots, - {f_{n - 1}}({ x}), \pm {f_n}({ x})]^{\rm{T}}}$ 。

在文献[11]中，已经证明了 ${f_n}({ x})$ 在沿曲线 $l$ 方向的导数满足：

式中： ${\Delta _{ni}}({{x}})(i = 1,\cdots,n)$ 由 ${{J}}({{x}})$ 中最后一行元素组成。

由式（3）可知，式（2）中 ${f_n}({{x}})$ 取负号时， ${f_n}({{x}})$ 沿曲线 $l$ 吸引到0；式（2）中 ${f_n}({{x}})$ 取正号时， ${f_n}({{x}})$ 沿曲线 $l$ 远离0。文献[11]已证明在搜索过程中，式（2）中 ${f_n}({{x}})$ 的符号改变发生在雅克比矩阵 ${{J}}({{x}})$ 的行列式改变符号时或找到了方程的解时。

2 算法求解

兼顾截断精度和计算量，采用四阶显式龙格库塔法^[12]求解初值问题式（4）的数值解。因为隐式积分方法要求对电路进行二阶灵敏度分析，其无法对式（4）进行求解。考虑到测试式（1）的代数方程无法准确得到，测点电压 ${{\hat f}_i}({{x}})(i = 1,\cdots,n)$ 以及 ${{\hat f}_i}({{x}})$ 对参数 ${x_j}(j = 1,\cdots,n)$ 的偏导数需要通过对给定参数 ${x_1}, \cdots ,{x_n}$ 的电路进行仿真，通过直流和灵敏度分析得到，即得到了 ${{w}}({{x}})$ 和 ${{J}}({{x}})$ 。

为了找到测试方程的所有可行解，本文提出采用系统搜索方法，关键是找到简单的空间曲线 $l$ 。否则，如果曲线 $l$ 是多分枝的，可能会失去部分解。因此，本文提出了一种产生多个简单曲线的方法，生成的每条曲线都可能找到多个解。考虑含 $n - 1$ 个方程的系统：

选择某参数取标称值，其余参数为变量，对该方程组进行 $n$ 次求解。例如，首先设置 ${x_n} = x_n^{\rm{nom}}$ ，针对参数 ${x_1},{x_2}, \cdots ,{x_{n - 1}}$ ，采用牛顿法解式（6），得到解 $x_1^ * ,x_2^ * , \cdots ,x_{n - 1}^ * $ ，与 $x_n^{\rm{nom}}$ 组成初值向量 ${ x}(0)$ ，该向量在空间曲线 $l$ （标记为 ${l^{(1)}}$ ，见式（2））上定义了起始点，使用第1节描述的搜索方法，产生空间曲线 ${l^{(1)}}$ ，得到式（1）的一个或多个解；为找到其他可能的解，设置 ${x_{n - 1}} = x_{n - 1}^{\rm{nom}}$ ，针对参数 ${x_1},{x_2}, \cdots ,{x_{n - 2}},{x_n}$ ，解式（6），得到新的向量，采用上述过程产生空间曲线 ${l^{(2)}}$ 。最后是设置 ${x_1} = x_1^{\rm{nom}}$ ，考虑参数 ${x_2},\cdots,{x_n}$ 。上述 $n$ 次求解方程组的过程中，如果遇到牛顿法发散，则舍弃该结果。

为简化说明，式（6）的系统用以下形式描述： ${{p}}({{x}}) = 0$ ，其中 ${{p}}({{x}}) = {[{f_1}({{x}}),\cdots,{f_{n - 1}}({{x}})]^{\rm{T}}}$ 。此外，用 ${{{x}}_{ - k}}$ 表示向量 ${[{x_1}, \cdots ,{x_{k - 1}},x_k^{\rm{nom}},{x_{k + 1}}, \cdots, {x_n}]^{\rm{T}}}$ ，由解 ${{x}}_{ - k}^ * $ 得到的空间曲线表示为 ${l^{(n - k + 1)}}$ 。沿着曲线 ${l^{(n - k + 1)}}$ ， $k \in \{ n,n - 1,\cdots,1\} $ ，采用系统搜索方法能够找到方程 ${{f}}({{x}}) = 0$ 的解。该方法从空间曲线的初始点开始，分别从两个方向进行跟踪。首先，将负号赋予 ${f_n}({{x}})$ ，求解式（4），跟踪曲线，该曲线标记为N部分；之后，将正号赋予 ${f_n}({{x}})$ ，选择同样的起始点，求解式（4），跟踪曲线，该曲线标记为P部分。当获得一个解时，搜索过程暂时锁定，检验是否满足物理限制条件。如果解不被接受，过程解锁并继续。如果计算步长m达到最大值 ${\tilde{ M}}$ ，该过程从起始点开始搜索曲线的P部分。当总步长 ${ m = M} = 2{\tilde{ M}}$ 时，方法锁定。因此，模块的输出量是搜索次数 $m$ 和方程解（ $m < M$ 时）。 $M$ 的选择基于数值仿真实验。

实际应用中测量精度有限，且考虑元件存在容差，因此对上述方法进行修正。对于曲线上的任何点 $x$ ，检测是否满足 ${{\hat f}_n}({{x}}) \in [{u_n} - \Delta {u_n},{u_n} + \Delta {u_n}]$ ，其中 $\Delta {u_n}$ 依赖于测量精度，而不是检测是否满足 ${f_n}({{x}}) = $ $ {{\hat f}_n}({{x}}) - {u_n} = 0$ 。基于大量数值仿真实验， $\Delta {u_n}$ 设置为 $5\varepsilon $ ，其中 $\varepsilon $ 为测量精度。通常，曲线上的若干点满足这一条件，而且所有点都必须视为测试方程的合适解。因此，不同于理想情况，得到参数范围集合 $\{ [x_1^ - ,x_1^ + ],\cdots,[x_n^ - ,x_n^ + ]\} $ 而不是一系列具体值。计算中值 ${\bar x_i} = (1/2)(x_i^ - + x_i^ + ),i = 1,\cdots,n$ ，考虑 ${ x} = {[{\bar x_1}, \cdots, {\bar x_n}]^{\rm{T}}}$ 为方程的合适解。

3 故障辨识

诊断的目的是找到电路中满足测试方程的可能发生故障的参数 ${x_1},\cdots{x_n}$ 的实际值，它们是非线性代数式（1）的解。由于方程可能存在多解，因此需考虑如何从中找到真实解。采用上述广义系统搜索方法寻找到方程解后，利用文献[13]中方法进行故障验证。

考虑电路中所有元件参数在容差范围内扰动，由文献[13]得到：

式中：y_i——第i个激励信号下测量值与标称参数下测量值的偏差；

x_j——第j个元件的参数偏差；

a_ij——第i个激励信号下电压e_i对第j个元件参数的电压灵敏度；

m——激励信号数量。

容差模拟电路正常状态下的元件参数偏差满足 $ -\varepsilon _{j}^{\rm{-}}\leqslant {{x}_{j}}\leqslant \varepsilon _{j}^{+}$ （j=1,···, n），其中 $ \varepsilon _{j}^{\rm{+}}$ 和 $ -\varepsilon _{j}^{\rm{-}}$ 分别表示参数容差的上下限值。判断式（7）解中所有参数偏差是否在容差范围内即可定位到故障元件。考虑将电路故障状态验证转化为容差约束下的线性规划问题求解。

引入变量 $ {{\tilde x}_j} = {x_j} + \varepsilon _j^{\rm{ - }}$ ，带入式（7），得到：

为判断式（8）解的存在性，采用单纯形法的第一阶段方法进行求解。引入人工变量z_i，对疑似故障元件k和l的参数偏差限值 $ \left( { - \varepsilon _k^{\rm{ - }},\varepsilon _k^{\rm{ + }}} \right)$ 和 $ \left( { - \varepsilon _l^{\rm{ - }},\varepsilon _l^{\rm{ + }}} \right)$ 进行修正，得到修正后的偏差限值为 $ \left( { - \gamma _k^{\rm{ - }},\gamma _k^{\rm{ + }}} \right)$ 和 $ \left( { - \gamma _l^{\rm{ - }},\gamma _l^{\rm{ + }}} \right)$ ，得到辅助线性规划方程：

若修正后的式（9）存在最小目标值Z≈0，则表示元件k和l确实发生故障。电路中存在更多故障的诊断过程与此类似。

4 实例验证

本文提出的算法使用大量BJT和CMOS电路进行测试。为了说明算法的有效性，考虑两个数值例子。在所有例子中，BJT电路的步长为0.01，CMOS的步长为0.05，M=20 000。

4.1 案例一

在实验室条件下搭建的BJT电路^[14]如图1所示。该电路含5个BC108B晶体管，测试电压精度为1 mV。考虑到电阻R₂、R₅和R₆的参数变化对输出电压的影响很小，故障无法检测，因此仅考虑电阻R₁、R₃和R₄可能发生故障情况。实际测量电阻值为R₂=5.024 kΩ，R₅=10.12 kΩ，R₆=99.8 kΩ。采用算法仿真计算时，采用它们的标称值。晶体管采用G-P模型，参数设置如下：IS=7.59×10⁻¹⁵ A，BF=480，NF=1，VAF=19.3 V，IKF=0.071 A，ISE=7.477×10⁻¹⁵ A，NE=1.2，BR=5，NR=1，VAR=12.5 V，ISC=2.00×10⁻¹³ A，NC=1.3808，RB=0 Ω，RE=0 Ω，RC=0 Ω。选择 $\Delta {u_i}$ =5 mV。测试激励信号如表1所示，考虑两种故障情况，实验测量电压见表1。采用本文提出算法，计算得到结果如表2所示。可以看出，计算电阻范围基本涵盖了故障电阻实值，计算得最大误差为4.35%。

如果提高电压测量精度到0.01 mV，更多数量的参数故障能够被诊断出来。考虑R₁、R₂、R₃、R₄和R₅参数，激励信号、测量电压及计算结果如表3所示。可以看出，计算电阻范围基本涵盖了故障电阻实值，计算得最大误差为1.38%。在上述讨论的例子中，计算得到的结果都在曲线 ${l^{(1)}}$ 上。

仿真实验包括30个不同的故障模式，实验结果为：计算得到19个故障模式的参数值位于曲线 ${l^{(1)}}$ 上，11个故障模式的参数值位于曲线 ${l^{(2)}}$ 上。

4.2 案例二

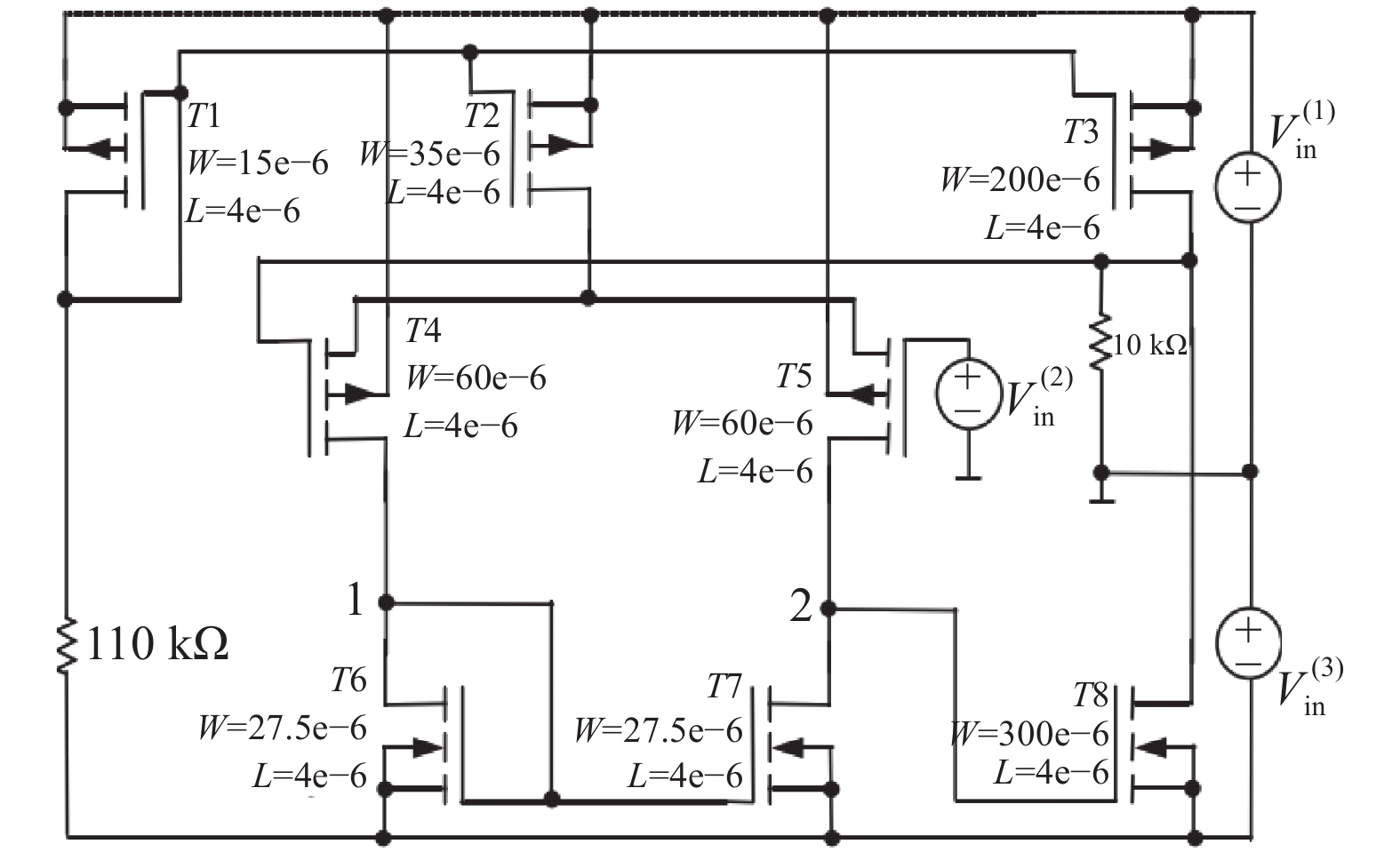
考虑如图2所示的含CMOS电压跟随器电路^[15]。MOS晶体管仿真采用PSPICE中的LEVEL 1模型，标称参数设置：pMOS-GAMMA=0.53 V^0.5，IS=10⁻¹⁶ A，KP=28.3 μA/V²，PHI=0.58 V，RD=RS=94 Ω，VTO=−0.84 V；nMOS-GAMMA=0.38 V^0.5，IS=10⁻¹⁶ A，KP=79.7 μA/V²，PHI=0.53 V，RD=RS=63 Ω，VTO=0.79 V。

晶体管标称每米的通道宽度和长度如图2所示。考虑沟道的宽度与长度的比值（W/L）偏差。晶体管的标称比值（W/L）为：3.750，8.750，50.000，15.000，15.000，6.875，6.875，75.000。

假设测点为1和2，测量精度取0.1 mV，测试安排如表4所示。假定晶体管T1、T5、T6、T7、T8可能发生故障，晶体管T2、T3、T4的宽度与长度的比值（W/L）取标称值，故障参数值位于曲线 ${l^{(2)}}$ 上，结果如表5所示。可以看出，W/L计算范围基本涵盖了实值，计算得最大误差为1.08%。

将测量精度提高到0.001 mV，测试安排如表6所示。假设所有的晶体管可能发生故障，该方法得到参数值范围（位于曲线 ${l^{(2)}}$ 上）如表7所示。可以看出，W/L计算范围基本涵盖了实值，计算得最大误差为1.16%。

仿真实验包括30个不同故障模式，实验结果为：计算得到24个故障模式的参数值位于曲线 ${l^{(1)}}$ 上，6个故障模式的参数值位于曲线 ${l^{(2)}}$ 上。

5 结束语

模拟电路参数故障诊断的关键是求解可能存在多解的非线性测试方程组，并从所有解中辨识出真解。本文研究将非线性测试方程的多解求解转化为差分方程的初值问题，提出一种系统搜索算法求解故障元件参数，将故障验证转化为线性规划问题最优解的存在性判断，BJT和CMOS电路实验验证了算法的有效性。本方法能够有效处理非线性模拟电路的软故障诊断问题，后续将进一步完善工程化的试验研究和对比分析。