中国测试  2019, Vol. 45 Issue (8): 93-99

文章信息

张涛, 王新华, ZIA Ullah
ZHANG Tao, WANG Xinhua, ZIA Ullah
测量多阶磁梯度张量的磁传感器阵列
A sensor array for multiple-order magnetic gradient tensor measurement
中国测试, 2019, 45(8): 93-99
CHINA MEASUREMENT & TEST, 2019, 45(8): 93-99
http://dx.doi.org/10.11857/j.issn.1674-5124.2018110073

文章历史

收稿日期: 2018-11-22
收到修改稿日期: 2019-01-18
 Abstract              PDF               Figures               Tables
引用本文 0
张涛, 王新华, ZIA Ullah. 测量多阶磁梯度张量的磁传感器阵列[J]. 中国测试, 2019, 45(8): 93-99.
ZHANG Tao, WANG Xinhua, ZIA Ullah. A sensor array for multiple-order magnetic gradient tensor measurement[J]. CHINA MEASUREMENT & TEST, 2019, 45(8): 93-99.
测量多阶磁梯度张量的磁传感器阵列
张涛 , 王新华 , ZIA Ullah     
北京工业大学机械工程与应用电子技术学院，北京 100124
收稿日期：2018-11-22; 收到修改稿日期：2019-01-18
基金项目：国家重点研发计划项目（2017YFC0805005-1）；北京市教育委员会科研计划项目资助（KZ201810005009）；中国博士后基金（2018T110020）
作者简介：张　涛（1989-），男，山西太原市人，博士研究生，研究方向为管道地磁检测。
通信作者：王新华（1969-），男，山东德州市人，教授，博士，研究方向为管道无损检测、流体传动与控制。
摘要：为实现多阶磁梯度张量的准确测量，提出一种磁传感器阵列。阵列由9个三轴磁传感器组成，在平面呈菱形排列。根据张量对称性，提出一阶及二阶磁梯度张量计算方法。采用Floater-Hormann有理插值完成测量盲点的修正。根据磁偶极子原理建立仿真模型，研究阵列在地磁场和噪声背景下的一阶及二阶磁梯度张量测量精度。仿真结果表明，提出阵列在磁梯度张量测量精度、完整性方面优于十字形阵列和六面体阵列。基于一阶和二阶磁梯度张量的定位应用也可证明所提出阵列的有效性。
关键词：传感器阵列    一阶磁梯度张量    二阶磁梯度张量    地磁场    插值    磁源定位    
A sensor array for multiple-order magnetic gradient tensor measurement
ZHANG Tao , WANG Xinhua , ZIA Ullah     
Department of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, China
Abstract: A magnetic sensor array was proposed to measure multiple-order magnetic gradient tensor (MGT) accurately. The array was composed of 9 three-axis magnetic sensors and arranged in the form of diamond on the plane. According to tensor symmetry, the calculation method of different-order MGT was proposed. Floater-Hormann rational interpolation was adopted to complete blind spot amendment. According to simulation model based on magnetic dipole theory, the effectiveness of first-order and second-order MGT was researched under geomagnetic field and noise backgrounds. The simulation results showed that the proposed array outperforms cross and hexahedron array in terms of measurement precision and integrity. The application of magnetic source positioning based on first-order and second-order MGT was carried out to illustrate the proposed array of effectiveness.
Key words: sensor array     first-order magnetic gradient tensor     second-order magnetic gradient tensor     geomagnetic field     interpolation     magnetic source positioning    
0 引　言

磁梯度张量由多阶磁场分量在不同方向上的空间变化率组成，相比于单分量磁场和总磁场，磁梯度张量包含丰富的磁场信息和诸多旋转不变量，被广泛应用于无损检测[1-2]、磁偶极子源定位[3-4]、磁性体几何参数反演[5]等领域。

磁梯度张量测量阵列通过捷联于载体上的多个磁传感器间接得到磁场梯度。一阶磁梯度张量是在实际应用中最常用的测量量。陈海龙等[6]采用两个三轴磁场传感器测量磁场，根据张量缩并理论求取磁梯度张量模量，并利用局部波数实现缺陷定位。但该阵列结构需保持磁传感器移动速度恒定，不具备实用性。于振涛等[7]利用等边三角形阵列，计算连续3个测量点的磁梯度张量，实现运动测量平面的磁偶极子源定位。但该阵列计算的磁梯度张量方法繁琐，误差较大。YIN等[8]利用十字形阵列计算单位磁矩向量和单位距离向量，在此基础上利用最小二乘法完成了磁性目标定位。LIU等[9]采用多组并联的十字形阵列结构，利用磁梯度张量各分量观测值与理论值差值的平方和作为目标优化函数，利用粒子群优化算法完成目标车辆位置的反演。万成彪等[10]通过十字形阵列计算磁梯度张量矩阵特征值，进一步得到位置方向矢量，实现磁性目标定位。NARA等[11]通过六面体阵列计算一阶磁梯度张量实现电磁线圈定位。但是，在遇到强噪声时，十字形阵列和六面体阵列会存在较大误差。

二阶磁梯度张量同样在定位中具有重要的应用，SUI等[12]利用安装在刻度盘上的单轴传感器和泰勒级数测量二阶磁梯度张量，实现了最大误差为0.8 cm的高精度定位。但是，此系统需要精确控制传感器旋转角度，缺乏实用性。YIN等[13]设计了十字形的磁梯度张量系统，利用一阶张量间的差分获得部分二阶磁梯度张量。但是，由于十字形阵列测量的一阶磁梯度张量存在较大误差，此方法会进一步扩大误差。此外，十字形阵列只能获取部分二阶磁梯度张量，导致其应用场合有限。

鉴于此，本文提出一种磁传感器测量阵列，研究了一阶及二阶磁梯度张量的计算方法。采用Floater-Hormann有理插值完成盲点的修正，并通过仿真验证了所提阵列能够完成高精度及完整的一阶及二阶磁梯度张量测量。此外，磁源定位应用的结果也表明所提阵列相比于其他阵列更加适合作为磁梯度张量测量阵列。

1 磁梯度张量

磁感应强度Bx, By，Bz在3个方向x, y, z的变化率为一阶磁梯度张量，其表达式[14]为

${{G}} = \left[ {\begin{aligned} {\displaystyle\frac{{\partial {{{B}}_x}}}{{\partial x}}}\quad{\displaystyle\frac{{\partial {{{B}}_x}}}{{\partial y}}}\quad{\displaystyle\frac{{\partial {{{{ B}}}_x}}}{{\partial {\textit z}}}} \\ {\displaystyle\frac{{\partial {{{B}}_y}}}{{\partial x}}}\quad{\displaystyle\frac{{\partial {{{B}}_y}}}{{\partial y}}}\quad{\displaystyle\frac{{\partial {{{B}}_y}}}{{\partial {\textit z}}}} \\ {\displaystyle\frac{{\partial {{{B}}_{\textit z}}}}{{\partial x}}}\quad{\displaystyle\frac{{\partial {{{B}}_{\textit z}}}}{{\partial y}}}\quad{\displaystyle\frac{{\partial {{{B}}_{\textit z}}}}{{\partial {\textit z}}}} \end{aligned}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{B}}_{xx}}}&{{{{B}}_{xy}}}&{{{{B}}_{x{\textit z}}}} \\ {{{{B}}_{yx}}}&{{{{B}}_{yy}}}&{{{{B}}_{y{\textit z}}}} \\ {{{{B}}_{{\textit z}x}}}&{{{{B}}_{{\textit z}y}}}&{{{{B}}_{{\textit z}{\textit z}}}} \end{array}} \right]$ (1)

在没有空间电流密度的观测区域，磁场的散度和旋度都为0，因此磁梯度张量分量具有对称性。式(1)可改写为

${{G}} = \left[ {\begin{array}{*{20}{c}} {{{{B}}_{xx}}}&{{{{B}}_{xy}}}&{{{{B}}_{{\textit z}x}}} \\ {{{{B}}_{yx}}}&{{{{B}}_{yy}}}&{{{{B}}_{{\textit z}y}}} \\ {{{{B}}_{{\textit z}x}}}&{{{{B}}_{{\textit z}y}}}&{ - {{{B}}_{xx}} - {{{B}}_{yy}}} \end{array}} \right]$ (2)

二阶磁梯度张量是一阶磁梯度张量9个分量的空间导数，拥有27个分量。二阶磁梯度张量分量同样具有对称性，可表示为

${{{S}}_x} = \frac{{\partial {{G}}}}{{\partial x}} = \left[ {\begin{array}{*{20}{c}} {{{{B}}_{xxx}}}&{{{{B}}_{xyx}}}&{{{{B}}_{x{\textit z}x}}} \\ {{{{B}}_{xyx}}}&{{{{B}}_{yyx}}}&{{{{B}}_{y{\textit z}x}}} \\ {{{{B}}_{x{\textit z}x}}}&{{{{B}}_{y{\textit z}x}}}&{ - {{{B}}_{xxx}} - {{{B}}_{yyx}}} \end{array}} \right]$ (3)
${{{S}}_y} = \frac{{\partial {{G}}}}{{\partial y}} = \left[ {\begin{array}{*{20}{c}} {{{{B}}_{xyx}}}&{{{{B}}_{yyx}}}&{{{{B}}_{y{\textit z}x}}} \\ {{{{B}}_{yyx}}}&{{{{B}}_{yyy}}}&{{{{B}}_{y{\textit z}y}}} \\ {{{{B}}_{y{\textit z}x}}}&{{{{B}}_{y{\textit z}y}}}&{ - {{{B}}_{xyx}} - {{{B}}_{yyy}}} \end{array}} \right]$ (4)
${{{S}}_{\textit z}} = \frac{{\partial {{G}}}}{{\partial {\textit z}}} = \left[ {\begin{array}{*{20}{c}} {{{{B}}_{x{\textit z}x}}}\!\!&\!\!{{{{B}}_{y{\textit z}x}}}\!\!&\!\!{ - {{{B}}_{xxx}} - {{{B}}_{yyx}}} \\ {{{{B}}_{y{\textit z}x}}}\!\!&\!\!{{{{B}}_{y{\textit z}y}}}\!\!&\!\!{ - {{{B}}_{xyx}} - {{{{ B}}}_{yyy}}} \\ { - {{{B}}_{xxx}} - {{{B}}_{yyx}}}\!\!&\!\!{ - {{{B}}_{xyx}} - {{{B}}_{yyy}}}\!\!&\!\!{ - {{{B}}_{x{\textit z}x}} - {{{B}}_{y{\textit z}y}}} \end{array}} \right]$ (5)
2 张量计算方法

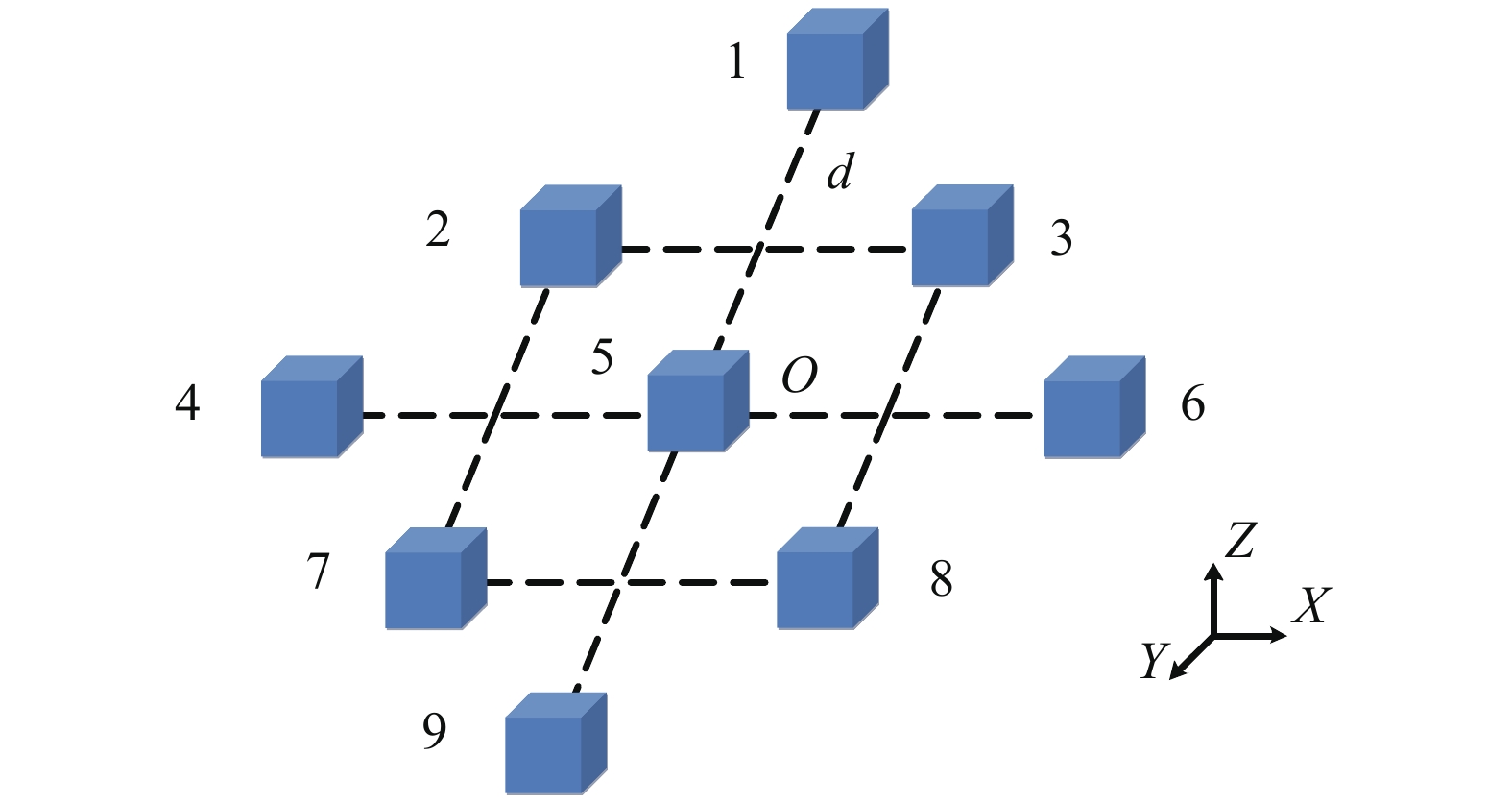
阵列由9个三轴磁场传感器构成，在平面形成菱形排列，其结构如图1所示。

图 1 磁梯度张量测量阵列
图选项

一阶磁梯度张量可表示为

${{{G}}_1} = \left[ {\begin{aligned} &{\frac{{{{M}}_x^3 - {{M}}_x^1}}{{2d}}}\quad{\frac{{{{M}}_x^2 - {{M}}_x^4}}{{2d}}}\quad\quad\quad\quad{\frac{{{{M}}_{\textit z}^3 - {{M}}_{\textit z}^1}}{{2d}}} \\ & {\frac{{{{M}}_y^3 - {{M}}_y^1}}{{2d}}}\quad{\frac{{{{M}}_y^2 - {{M}}_y^4}}{{2d}}}\quad\quad\quad\quad{\frac{{{{M}}_{\textit z}^2 - {{M}}_{\textit z}^4}}{{2d}}} \\ &{\frac{{{{M}}_{\textit z}^3 - {{M}}_{\textit z}^1}}{{2d}}}\quad{\frac{{{{M}}_{\textit z}^2 - {{M}}_{\textit z}^4}}{{2d}}}\quad{ - \frac{{{{M}}_x^3 - {{M}}_x^1}}{{2d}} - \frac{{{{M}}_y^2 - {{M}}_y^4}}{{2d}}} \end{aligned}} \right]$ (6)

其中，2d为基线距离； $j = x,y,{\textit z}$ ，代表笛卡尔坐标中的三轴方向。

$\left\{ \begin{gathered} {{M}}_j^1 = ({{B}}_j^2 + {{B}}_j^4 + {{B}}_j^5 + {{B}}_j^7)/4 \\ {{M}}_j^2 = ({{B}}_j^5 + {{B}}_j^7 + {{B}}_j^8 + {{B}}_j^9)/4 \\ {{M}}_j^3 = ({{B}}_j^3 + {{B}}_j^5 + {{B}}_j^6 + {{B}}_j^8)/4 \\ {{M}}_j^4 = ({{B}}_j^1 + {{B}}_j^2 + {{B}}_j^3 + {{B}}_j^5)/4 \end{gathered} \right.$ (7)

二阶磁梯度张量可表示为

$ {{S}}_x^1 = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{{B}}_x^6 - 2{{B}}_x^5 + {{B}}_x^4}}{{4{d^2}}}}&{\displaystyle\frac{{{{{ B}}}_x^8 - {{B}}_x^3 - {{B}}_x^7 + {{B}}_x^2}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^6 - 2{{B}}_{\textit z}^5 + {{B}}_{\textit z}^4}}{{4{d^2}}}}\\ {\displaystyle\frac{{{{B}}_y^6 - 2{{B}}_y^5 + {{B}}_y^4}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_y^8 - {{B}}_y^3 - {{B}}_y^7 + {{B}}_y^2}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^8 - {{B}}_{\textit z}^3 - {{B}}_{\textit z}^7 + {{B}}_{\textit z}^2}}{{4{d^2}}}} \\ {\displaystyle\frac{{{{B}}_{\textit z}^6 - 2{{B}}_{\textit z}^5 + {{B}}_{\textit z}^4}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^8 - {{B}}_{\textit z}^3 - {{B}}_{\textit z}^7 + {{B}}_{\textit z}^2}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_x^6 + 2{{B}}_x^5 - {{B}}_x^4 - {{B}}_y^8 + {{B}}_y^3 + {{B}}_y^7 - {{B}}_y^2}}{{4{d^2}}}} \end{array}} \right] $ (8)
${{S}}_y^1 = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{{B}}_x^8 - {{B}}_x^7 - {{B}}_x^3 + {{B}}_x^2}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_x^9 - 2{{B}}_x^5 + {{B}}_x^1}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^8 - {{B}}_{\textit z}^7 - {{B}}_{\textit z}^3 + {{B}}_{\textit z}^2}}{{4{d^2}}}} \\ {\displaystyle\frac{{{{B}}_y^8 - {{B}}_y^7 - {{B}}_y^3 + {{B}}_y^2}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_y^9 - 2{{B}}_y^5+ {{B}}_y^1}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^9 - 2{{B}}_{\textit z}^5 + {{B}}_{\textit z}^1}}{{4{d^2}}}} \\ {\displaystyle\frac{{{{B}}_{\textit z}^8 - {{B}}_{\textit z}^7 - {{B}}_{\textit z}^3 + {{B}}_{\textit z}^2}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^9 - 2{{B}}_{\textit z}^5 +{{B}}_{\textit z}^1}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_x^8 + {{B}}_x^7 + {{B}}_x^3 - {{B}}_x^2 - {{B}}_y^9 + 2{{B}}_y^5 - {{B}}_y^1}}{{4{d^2}}}} \end{array}} \right]$ (9)
${{S}}_{\textit z}^1 = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{{B}}_{\textit z}^6 - 2{{B}}_{\textit z}^5 + {{B}}_{\textit z}^4}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^8 - {{B}}_{\textit z}^7 - {{B}}_{\textit z}^3 + {{B}}_{\textit z}^2}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_x^6 + 2{{B}}_x^5 - {{B}}_x^4 - {{B}}_y^8 + {{B}}_y^3 + {{B}}_y^7 - {{B}}_y^2}}{{4{d^2}}}} \\ {\displaystyle\frac{{{{B}}_{\textit z}^8 - {{B}}_{\textit z}^7 - {{B}}_{\textit z}^3 + {{B}}_{\textit z}^2}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^9 - 2{{B}}_{\textit z}^5 +{{B}}_{\textit z}^1}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_x^8 + {{B}}_x^7 + {{B}}_x^3 - {{B}}_x^2 - {{B}}_y^9 + 2{{B}}_y^5 - {{B}}_y^1}}{{4{d^2}}}} \\ {\displaystyle\frac{{ - {{B}}_x^6 \!+\! 2{{B}}_x^5\! -\! {{B}}_x^4 \!-\! {{B}}_y^8 \!+\! {{B}}_y^3 \!+\! {{B}}_y^7 \!-\! {{B}}_y^2}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_x^8 \!+\! {{B}}_x^7 \!+\! {{B}}_x^3\!-\! {{B}}_x^2 \!-\! {{B}}_y^9 \!+\! 2{{B}}_y^5 \!-\! {{B}}_y^1}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_{\textit z}^6 \!+\! 4{{B}}_{\textit z}^5 \!-\! {{B}}_{\textit z}^4 \!-\! {{B}}_{\textit z}^9 \!-\! {{B}}_{\textit z}^1}}{{4{d^2}}}} \end{array}} \right]$ (10)

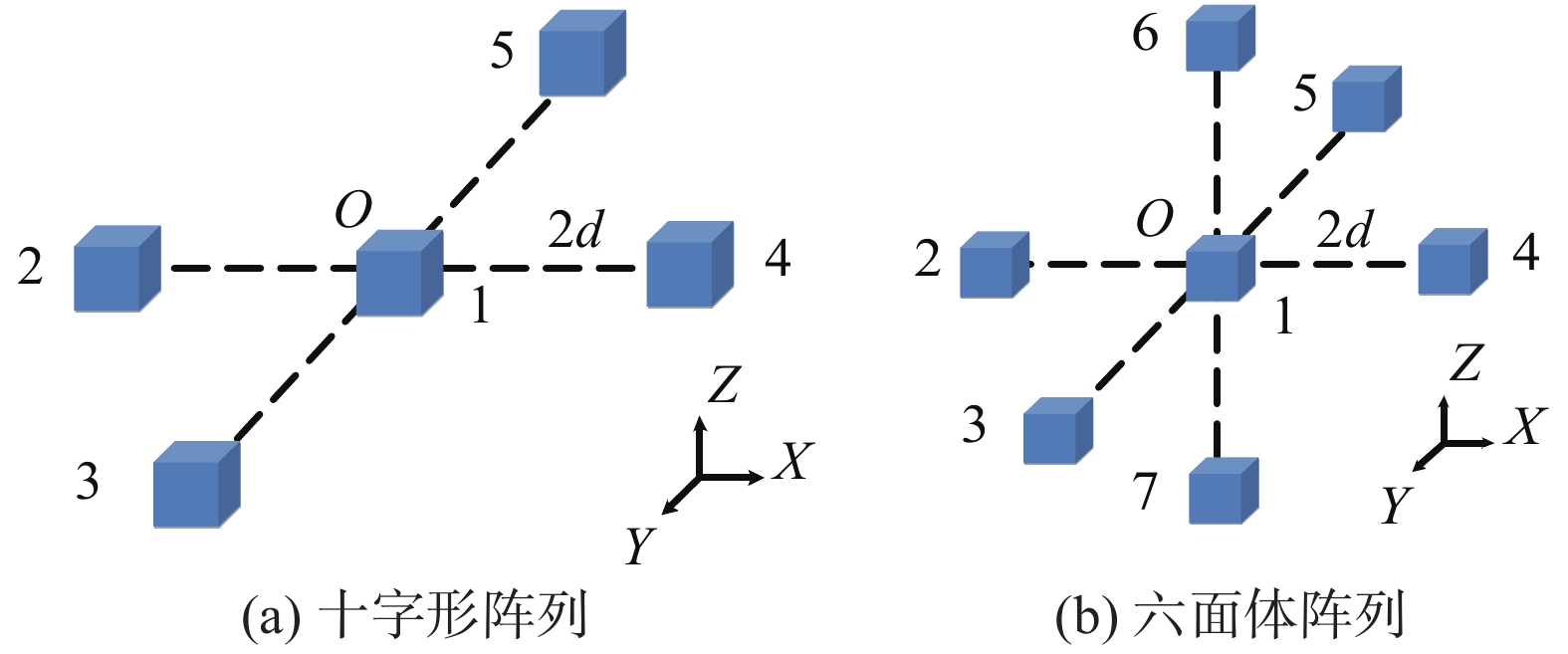
为更好地验证新阵列的有效性，引入十字形阵列和六面体阵列，其结构如图2所示。十字形阵列的一阶磁梯度张量可表示为

图 2 传统阵列结构
图选项

$ {{{G}}_2} = \left[ {\begin{array}{*{20}{c}} {{\rm{ }}\displaystyle\frac{{{{{ B}}}_x^4 - {{B}}_x^2}}{{4d}}}&{\displaystyle\frac{{{{B}}_x^3 - {{B}}_x^5}}{{4d}}}&{\displaystyle\frac{{{{B}}_{\textit z}^4 - {{B}}_{\textit z}^2}}{{4d}}} \\ {\displaystyle\frac{{{{B}}_y^4 - {{B}}_y^2}}{{4d}}}&{\displaystyle\frac{{{{B}}_y^3 - {{B}}_y^5}}{{4d}}}&{\displaystyle\frac{{{{B}}_{\textit z}^3 - {{B}}_{\textit z}^5}}{{4d}}} \\ {\displaystyle\frac{{{{B}}_{\textit z}^4 - {{B}}_{\textit z}^2}}{{4d}}}&{\displaystyle\frac{{{{B}}_{\textit z}^3 - {{B}}_{\textit z}^5}}{{4d}}}&{ - \displaystyle\frac{{{{B}}_x^4 - {{B}}_x^2}}{{4d}} - \frac{{{{B}}_y^3 - {{B}}_y^5}}{{4d}}} \end{array}} \right] $ (11)

十字形阵列无法计算完整二阶磁梯度张量，则部分二阶磁梯度张量的计算公式为

${{S}}_x^2 = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{{B}}_x^4 + {{B}}_x^2 - 2{{B}}_x^1}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_y^4 + {{B}}_y^2 - 2{{B}}_y^1}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^4 + {{B}}_{\textit z}^2 - 2{{B}}_{\textit z}^1}}{{4{d^2}}}} \\ {\displaystyle\frac{{{{B}}_y^4 + {{B}}_y^2 - 2{{B}}_y^1}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_x^3 + {{B}}_x^5 - 2{{B}}_x^1}}{{4{d^2}}}}&* \\ {\displaystyle\frac{{{{B}}_{\textit z}^4 + {{B}}_{\textit z}^2 - 2{{B}}_{\textit z}^1}}{{4{d^2}}}}&*&{\displaystyle\frac{{ - {{B}}_x^4 - {{B}}_x^2 + 4{{B}}_x^1 - {{B}}_x^3 - {{B}}_x^5}}{{4{d^2}}}} \end{array}} \right]$ (12)
${{S}}_y^2 = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{{B}}_y^4 + {{B}}_y^2 - 2{{B}}_y^1}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_x^3 + {{B}}_x^5 - 2{{B}}_x^1}}{{4{d^2}}}}&* \\ {\displaystyle\frac{{{{B}}_x^3 + {{B}}_x^5 - 2{{B}}_x^1}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_y^3 + {{B}}_y^5 - 2{{B}}_y^1}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^3 + {{B}}_{\textit z}^5 - 2{{B}}_{\textit z}^1}}{{4{d^2}}}} \\ *&{\displaystyle\frac{{{{B}}_{\textit z}^3 + {{B}}_{\textit z}^5 - 2{{B}}_{\textit z}^1}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_y^4 - {{B}}_y^2 + 4{{B}}_y^1 - {{B}}_y^3 - {{B}}_y^5}}{{4{d^2}}}} \end{array}} \right]$ (13)
${{S}}_ {\textit z}^2 = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{{B}}_{\textit z}^4 + {{B}}_{\textit z}^2 - 2{{B}}_{\textit z}^1}}{{4{d^2}}}}&*&{\displaystyle\frac{{ - {{B}}_x^4 - {{B}}_x^2 + 4{{B}}_x^1 - {{B}}_x^3 - {{B}}_x^5}}{{4{d^2}}}} \\ *&{\displaystyle\frac{{{{B}}_{\textit z}^3 + {{B}}_{\textit z}^5 - 2{{B}}_{\textit z}^1}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_y^4 - {{B}}_y^2 + 4{{B}}_y^1 - {{B}}_y^3 - {{B}}_y^5}}{{4{d^2}}}} \\ {\displaystyle\frac{{ - {{B}}_x^4 - {{B}}_x^2 + 4{{B}}_x^1 - {{B}}_x^3 - {{B}}_x^5}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_y^4 - {{B}}_y^2 + 4{{B}}_y^1 - {{B}}_y^3 - {{B}}_y^5}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_{\textit z}^4 - {{B}}_{\textit z}^2 + 4{{B}}_{\textit z}^1 - {{B}}_{\textit z}^3 - {{B}}_{\textit z}^5}}{{4{d^2}}}} \end{array}} \right]$ (14)

其中，*代表分量无法计算。同样的，六面体阵列的一阶磁梯度张量可表示为

${{{G}}_3} = \left[ {\begin{array}{*{20}{c}} { \displaystyle\frac{{{{B}}_x^4 - {{B}}_x^2}}{{4d}}}&{\displaystyle\frac{{{{B}}_x^3 - {{B}}_x^5}}{{4d}}}&{\displaystyle\frac{{{{B}}_x^6 - {{B}}_x^7}}{{4d}}} \\ {\displaystyle\frac{{{{B}}_y^4 - {{B}}_y^2}}{{4d}}}&{\displaystyle\frac{{{{B}}_y^3 - {{{\rm B}}}_y^5}}{{4d}}}&{\displaystyle\frac{{{{B}}_y^6 - {{B}}_y^7}}{{4d}}} \\ {\displaystyle\frac{{{{B}}_{\textit z}^4 - {{B}}_{\textit z}^2}}{{4d}}}&{\displaystyle\frac{{{{B}}_{\textit z}^3 - {{B}}_{\textit z}^5}}{{4d}}}&{\displaystyle\frac{{{{B}}_{\textit z}^6 - {{B}}_{\textit z}^7}}{{4d}}} \end{array}} \right]$ (15)

与十字形阵列相同，六面体阵列也只能计算部分二阶磁梯度张量，其中 ${{S}}_x^3$ 和 ${{S}}_y^3$ 与十字形阵列的 ${{S}}_x^2$ 和 ${{S}}_y^2$ 相同， ${{S}}_{\textit z}^3$ 可表示为

${{S}}_{\textit z}^3 = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{{B}}_{\textit z}^4 + {{B}}_{\textit z}^2 - 2{{B}}_{\textit z}^1}}{{4{d^2}}}}&*&{\displaystyle\frac{{{{B}}_x^6 + {{B}}_x^7 - 2{{B}}_x^1}}{{4{d^2}}}} \\ *&{\displaystyle\frac{{{{B}}_{\textit z}^3 + {{B}}_{\textit z}^5 - 2{{B}}_{\textit z}^1}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_y^6 + {{B}}_y^7 - 2{{B}}_y^1}}{{4{d^2}}}} \\ {\displaystyle\frac{{ - {{B}}_x^4 - {{B}}_x^2 + 4{{B}}_x^1 - {{B}}_x^3 - {{B}}_x^5}}{{4{d^2}}}}&{\displaystyle\frac{{ - {{B}}_y^4 - {{B}}_y^2 + 4{{B}}_y^1 - {{B}}_y^3 - {{B}}_y^5}}{{4{d^2}}}}&{\displaystyle\frac{{{{B}}_{\textit z}^6 + {{B}}_{\textit z}^7 - 2{{B}}_{\textit z}^1}}{{4{d^2}}}} \end{array}} \right]$ (16)
3 一阶磁梯度张量测量精度研究

设置仿真条件为：磁源位置为坐标原点，磁矩大小 ${{M}} = ( - 12500,12500,10000)\;{\rm{A}} \cdot {{\rm{m}}^2}$ 。测量平面为 $2\;{\rm{m}} \times 2\;{\rm{m}}$ 的正方形区域，测量高度为 $1\;{\rm{m}}$ ，每隔 $0.05\;{\rm{m}} \times 0.05\;{\rm{m}}$ 作为一个测量点。阵列基线距离 $d = 0.01\;{\rm{m}}$ ，误差公式为

$e = \frac{{\displaystyle\sum {\left| {({{{G}}_{ij - a}} - {{{G}}_{ij - t}})/{{{G}}_{ij - t}}} \right|} }}{9} \times 100\text{%} $ (17)

其中， ${{{G}}_{ij - a}}$ 和 ${{{G}}_{ij - t}}$ 分别为一阶磁梯度张量测量值和理论值。

3.1 Floater-Hormann有理插值

在测量过程中，某些点会使式(17)失去意义，这些点被称为盲点。采用Floater-Hormann有理插值方法[15]实现盲点的修正。区间 $[a,b]$ 有离散点：

$a = {x_0} < {x_1} < \cdots < {x_n} = b$ (18)

设 $0 \leqslant d \leqslant n$ ， ${p_i}(i = 0,1, \cdots n - d)$ 为在 $d + 1$ 个节点 ${x_i},{x_{i + 1}}, \cdots {x_{i + d}}$ 上的插值多项式，令：

$r(x) = \frac{{\displaystyle\sum\limits_{i = 0}^{n - d} {{\gamma _i}(x){p_i}(x)} }}{{\displaystyle\sum\limits_{i = 0}^{n - d} {{\gamma _i}(x)} }}$ (19)

其中：

${\gamma _i}(x) = \frac{{{{( - 1)}^i}}}{{(x - {x_i}) \cdots (x - {x_{i + d}})}}$ (20)

$r(x)$ 为多项式插值 ${p_0}, \cdots ,{p_{n - d}}$ 的融合函数。将多项式 $p_i$ 写成拉格朗日形式：

${p_i}(x) = \sum\limits_{k = i}^{i + d} {\prod\limits_{j = i,j \ne k}^{i + d} {\frac{{x - {x_j}}}{{{x_k} - {x_j}}}f({x_k})} } $ (21)

式(19)的分子和分母可表示为

$\begin{split} \sum\limits_{i = 0}^{n - d} {{\gamma _i}(x){p_i}(x)} =& {\sum\limits_{i = 0}^{n - d} {{{( - 1)}^i}} } \sum\limits_{k = i}^{i + d} {\frac{1}{{x - {x_k}}}} \prod\limits_{j = i,j \ne k}^{i + d} {\frac{1}{{{x_k} - {x_j}}}f({x_k})} = \\ & \sum\limits_{k = 0}^n {\frac{{{\omega _k}}}{{x - {x_k}}}f({x_k})} \end{split} $ (22)
$\sum\limits_{i = 0}^{n - d} {{\gamma _i}(x) = } \sum\limits_{k = 0}^n {\frac{{{\omega _k}}}{{x - {x_k}}}} $ (23)

其中：

${\omega _k} = {( - 1)^{k - d}}\sum\limits_{i \in {J_k}} {\prod\limits_{j = i,j \ne k}^{i + d} {\frac{1}{{\left| {{x_k} - {x_j}} \right|}}} } $ (24)

式中， ${J_k} = \left\{ {i \in I:k - d \leqslant i \leqslant k} \right\}$ ， $I = \left\{ {0,1, \cdots ,n - d} \right\}$ 。本文选用 $d = 4$ 进行有理插值，其权值系数为

$\left| {{\omega _k}} \right| = 1,5,11,15,16,16, \cdots ,16,16,15,11,5,1$ (25)
3.2 地磁场背景（一阶）

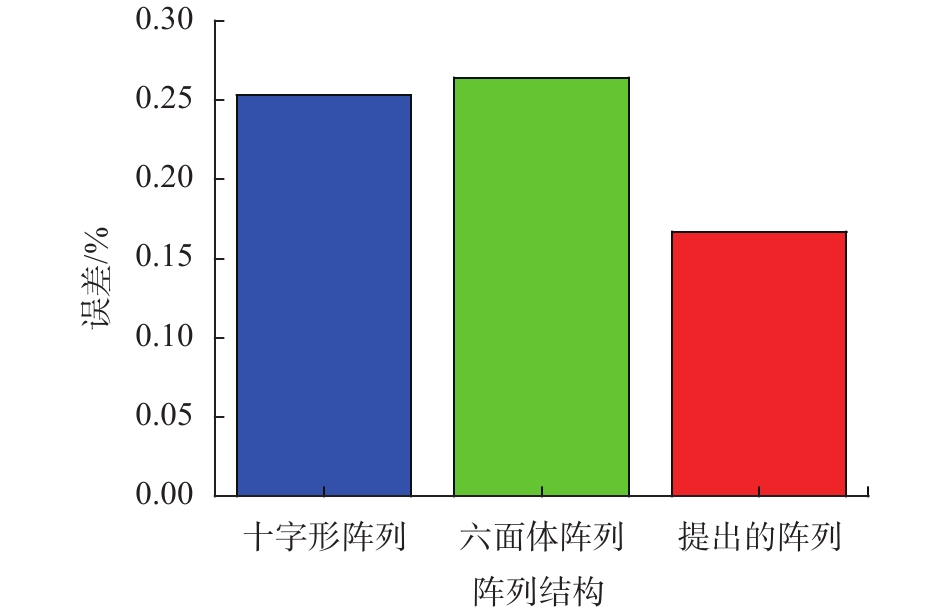
设置地磁场磁感应磁强度B= （27 961.9, −2 938.9, 46 792.8） nT。图3为十字形阵列、六面体阵列、提出阵列在地磁场背景下一阶磁梯度张量的平均测量误差。由图可知，十字形阵列平均误差为0.25%，六面体阵列平均误差为0.26%，而提出阵列平均误差仅为0.16%。综上所述，在地磁场背景下，提出阵列相比于十字形阵列和六面体阵列的一阶磁梯度张量测量精度更高。

图 3 地磁场背景下3种阵列的一阶磁梯度张量测量误差
图选项

3.3 噪声背景（一阶）

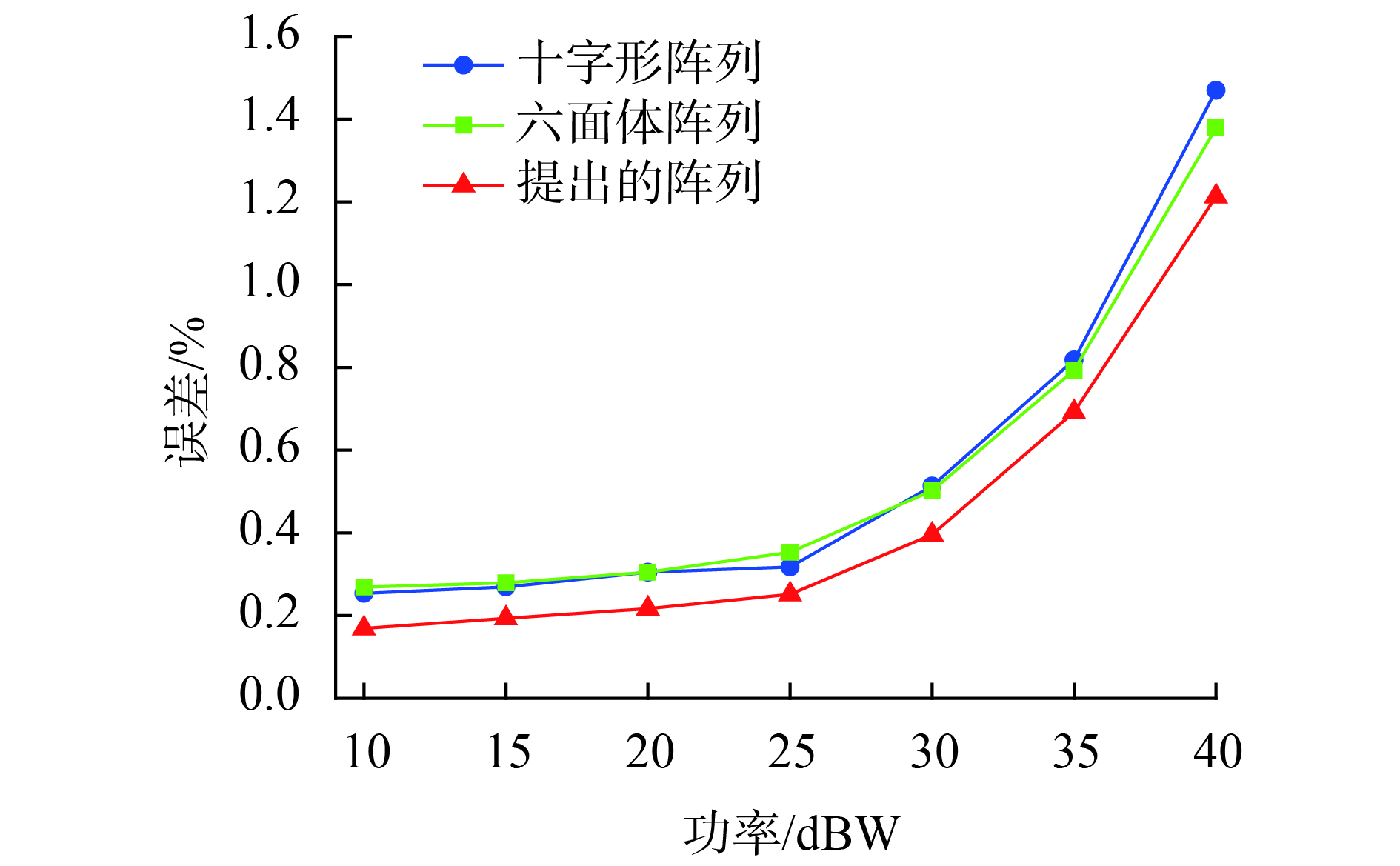
在实际检测中，测量信号中通常包含外界噪声。为了更全面地研究提出阵列的有效性，在地磁场背景下依次叠加噪声强度为10，15，20，25，30，35，40 dBW高斯白噪声，计算3种阵列的一阶磁梯度张量测量误差，其结果如图4所示。可以看出，随着噪声强度的增加，3种阵列的测量误差也逐渐增加。在任何强度的噪声背景下，十字形阵列和六面体阵列的平均误差相差很小，但提出阵列明显减小。特别地，在最高强度40 dBW情况下，提出阵列的误差分别小于十字形阵列17.5%和六面体阵列12%。因此，提出阵列能够更加精确地测量噪声背景下的一阶磁梯度张量。

图 4 噪声背景下3种阵列的一阶磁梯度张量测量误差
图选项

4 二阶磁梯度张量测量精度研究

二阶磁梯度张量分量测量值 ${{{G'}}_{ijk - a}}$ 与理论值 ${{{G'}}_{ijk - t}}$ 间误差公式为

$e = \frac{{\displaystyle\sum {\left| {({{{{G'}}}_{ijk - a}} - {{{{G'}}}_{ijk - t}})/{{{{G'}}}_{ijk - t}}} \right|} }}{{21}} \times 100\text{%} $ (26)

根据式(12)~式(14)和式(16)，十字形阵列和六面体阵列无法测量 ${ B_{xy{\textit z}}}$ ，所以设置式(26)的分母为21。

4.1 地磁场背景（二阶）

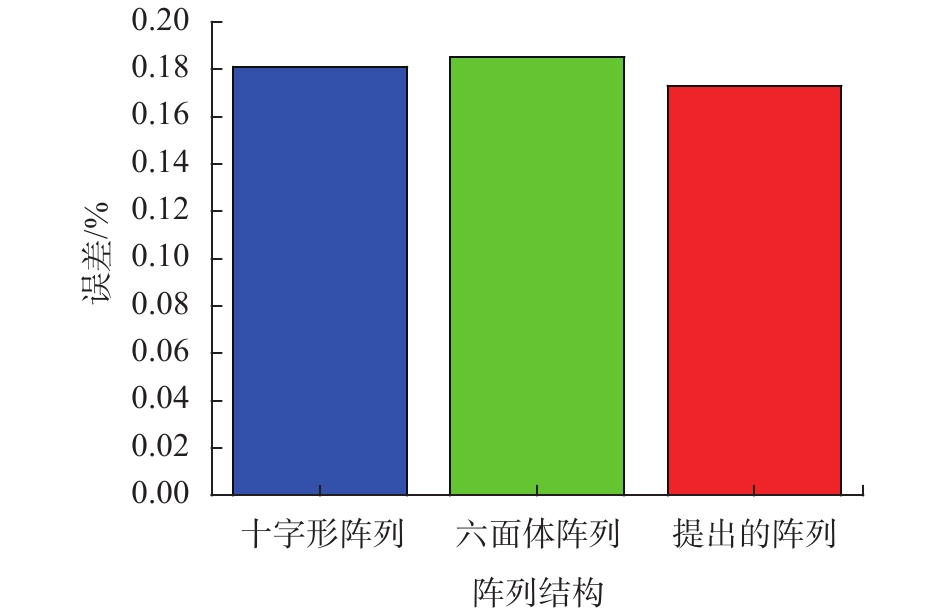
采用与3.2节相同的仿真条件，计算地磁场背景下3种阵列的二阶磁梯度张量的平均测量误差，其结果如图5所示。可以看出，十字形和提出阵列的平均误差分别为0.180%和0.185%，提出阵列的最大误差为0.173%。因此，提出阵列的二阶磁梯度张量的测量精度相比于其他两种阵列有了进一步提高。

图 5 地磁场背景下3种阵列的二阶磁梯度张量测量误差
图选项

4.2 噪声背景（二阶）

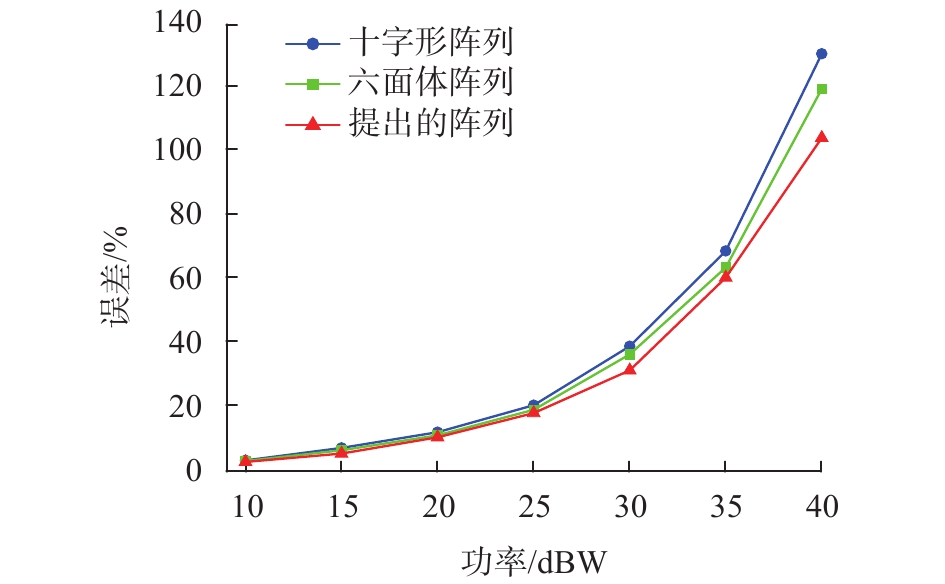
采用与3.3节相同的仿真条件，计算不同强度噪声背景下3种阵列的二阶磁梯度张量测量误差，其结果如图6所示。可以看出，在任何强度的噪声背景下，提出阵列的误差都要比十字形阵列和六面体阵列的小。在噪声环境最复杂的情况（40 dBW）下，提出阵列的平均误差分别小于十字形阵列20.4%和六面体阵列12.8%。同时，由于提出阵列能够完整计算二阶张量各分量，因此更适合作为二阶磁梯度张量的测量阵列。

图 6 噪声背景下3种阵列的二阶磁梯度张量的测量误差
图选项

5 应　用 5.1 定位原理

利用基于一阶及二阶磁梯度张量的磁源定位验证提出阵列有效性。当磁源与测量点距离远大于磁源尺寸的2.5倍时，磁源可认为是磁偶极子。磁偶极子定位[16]可以表示为

$ \begin{split} &{{r}} = \left[ {\begin{array}{*{20}{c}} {{{{r}}_x}} \\ {{{{r}}_y}} \\ {{{{r}}_{\textit z}}} \end{array}} \right] = - 4{\left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{\partial {{{B}}_{xx}}}}{{\partial i}}}&{\displaystyle\frac{{\partial {{{B}}_{xy}}}}{{\partial i}}}&{\displaystyle\frac{{\partial {{{B}}_{x{\textit z}}}}}{{\partial i}}} \\ {\displaystyle\frac{{\partial {{{B}}_{yx}}}}{{\partial j}}}&{\displaystyle\frac{{\partial {{{B}}_{yy}}}}{{\partial j}}}&{\displaystyle\frac{{\partial {{{B}}_{y{\textit z}}}}}{{\partial j}}} \\ {\displaystyle\frac{{\partial {{{B}}_{{\textit z}x}}}}{{\partial k}}}&{\displaystyle\frac{{\partial {{{B}}_{{\textit z}y}}}}{{\partial k}}}&{\displaystyle\frac{{\partial {{{B}}_{{\textit z}{\textit z}}}}}{{\partial k}}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{\partial {{{B}}_x}}}{{\partial i}}} \\ {\displaystyle\frac{{\partial {{{B}}_y}}}{{\partial j}}} \\ {\displaystyle\frac{{\partial {{{B}}_{\textit z}}}}{{\partial k}}} \end{array}} \right] \end{split} $ (27)

式(27)为超定方程，可以通过最小二乘法求解。考虑只有提出阵列能够测量 ${{ B}_{xy{\textit z}}}$ ，所以十字形阵列和六面体阵列的定位公式可简化为

${{r}} = \left[ {\begin{array}{*{20}{c}} {{{{r}}_x}} \\ {{{{r}}_y}} \\ {{{{r}}_{\textit z}}} \end{array}} \right] = - 4{\left[ {\begin{array}{*{20}{c}} {{{{B}}_{xxx}}}&{{{{B}}_{xyx}}}&{{{{B}}_{x{\textit z}x}}} \\ {{{{B}}_{yxy}}}&{{{{B}}_{yyy}}}&{{{{B}}_{y{\textit z}y}}} \\ {{{{B}}_{{\textit z}x{\textit z}}}}&{{{{B}}_{{\textit z}y{\textit z}}}}&{{{{B}}_{{\textit z}{\textit z}{\textit z}}}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{{{B}}_{xx}}} \\ {{{{B}}_{yy}}} \\ {{{{B}}_{{\textit z}{\textit z}}}} \end{array}} \right]$ (28)
5.2 结果与讨论

设置磁源位置为坐标原点，磁矩大小 ${{M}} = ( - 12\;500,12\;500,10\;000)\;{\rm{A}} \cdot {{\rm{m}}^2}$ 。测量平面为10 m×10 m 的正方形区域，测量高度为 $1\;{\rm{m}}$ ，每隔 $0.1\;{\rm{m}} \times 0.1\;{\rm{m}}$ 作为一个测量点。阵列基线距离 $d = 0.01\;{\rm{m}}$ 。定位误差可表示为

$e = \sqrt {\sum {{{({L_{mi}} - {L_{ti}})}^2}} } $ (29)

其中， ${L_{mi}}$ 和 ${L_{ti}}$ 分别为测量与实际的磁源位置。

1）地磁场背景

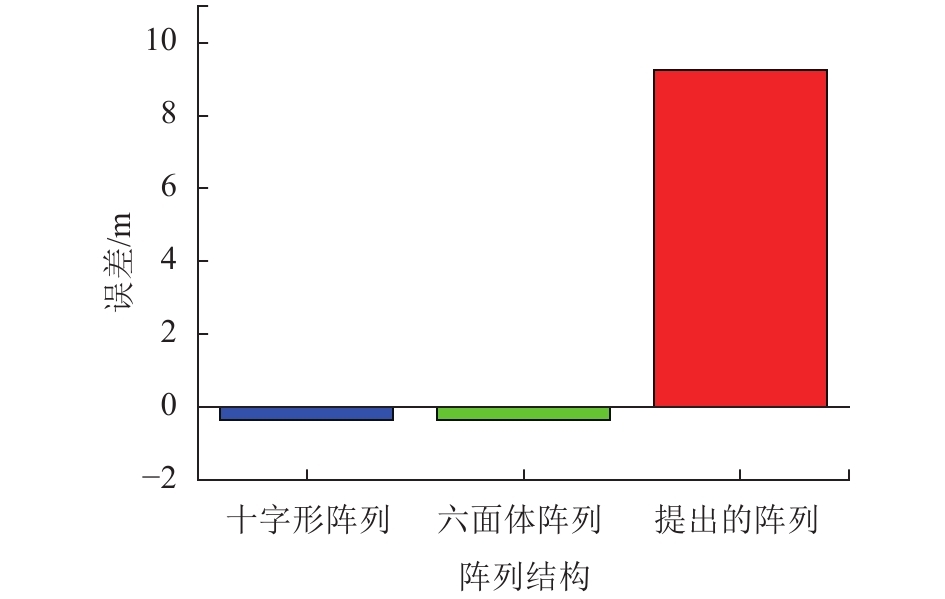
设置地磁场背景同3.2节一致，计算地磁场背景下3种阵列的定位误差。由于提出阵列的平均误差远小于其他两个阵列，所以对平均误差进行对数并取反运算，结果如图7所示。优化后误差越大代表实际定位误差越小。可以看出，3种阵列优化后的平均误差分别为−0.361 6 m、−0.352 8 m、9.250 8 m。因此，在地磁场背景下提出阵列的定位精度高于其他两种阵列。

图 7 地磁场背景下3种阵列的定位误差
图选项

2）噪声背景

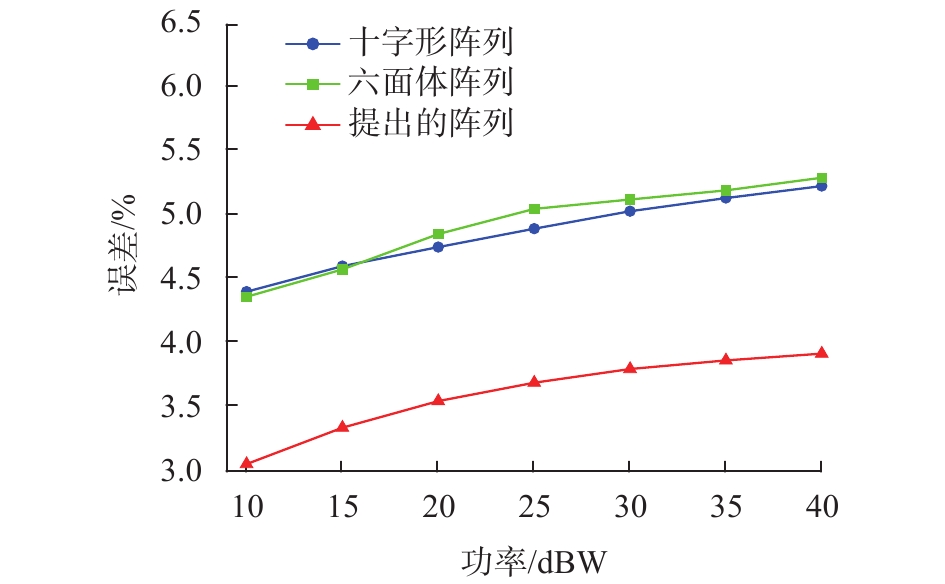
设置噪声背景与3.3节相同。噪声背景下3种阵列的定位误差如图8所示。可以看出，在不同噪声环境下，提出阵列的定位误差比其他两种阵列的误差小。在最高强度40 dBW的情况下，提出阵列的平均定位误差分别小于十字形阵列25.1%和六面体阵列26%。相比于十字形阵列和六面体阵列，由于提出阵列能够完整测量二阶磁梯度张量，因此能够完成更加精确的磁源定位。

图 8 噪声背景下3种阵列的定位误差
图选项

6 结束语

本文提出一种传感器阵列用于测量多阶磁梯度张量。根据磁梯度张量性质，提出了一阶及二阶磁梯度张量计算方法。采用Floater-Hormann有理插值完成盲点修正，通过仿真得到了如下结论：

1）在地磁场及不同强度噪声的背景场下，提出阵列的一阶磁梯度张量平均测量误差小于十字形阵列和六面体阵列。

2）提出阵列相比于十字形阵列和六面体阵列在完整性及测量精度方面更适合作为二阶磁梯度张量的测量阵列。

3）在不同背景场下的磁源定位的应用中，提出阵列的位置反演误差相比于十字形阵列和六面体阵列小，也证明了提出阵列能够完成高精度的多阶磁梯度张量测量。

参考文献
[1]
陈海龙, 王长龙, 左宪章, 等. 磁记忆梯度张量测量信号预处理方法[J]. 系统工程与电子技术, 2017, 39(3): 488-493. DOI:10.3969/j.issn.1001-506X.2017.03.05
[2]
SONG Q, DING W, PENG H, et al. A new magnetic testing technology based on magnetic gradient tensor theory[J]. Insight - Non-Destructive Testing and Condition Monitoring, 2017, 59(6): 325-329. DOI:10.1784/insi.2017.59.6.325
[3]
LEE K, LI M. Magnetic tensor sensor for gradient-based localization of ferrous object in geomagnetic field[J]. IEEE Transactions on Magnetics, 2016, 52(8): 1-10.
[4]
张朝阳, 肖昌汉, 阎辉. 磁性目标的单点磁梯度张量定位方法[J]. 探测与控制学报, 2009, 31(4): 44-48. DOI:10.3969/j.issn.1008-1194.2009.04.011
[5]
MA G, DU X. An improved analytic signal technique for the depth and structural index from 2D magnetic anomaly data[J]. Pure & Applied Geophysics, 2012, 169(12): 2193-2200.
[6]
陈海龙, 王长龙, 朱红运. 基于磁梯度张量的金属磁记忆检测方法[J]. 仪器仪表学报, 2016, 37(3): 602-609. DOI:10.3969/j.issn.0254-3087.2016.03.017
[7]
于振涛, 吕俊伟, 许素芹, 等. 运动平台的磁性目标实时定位方法[J]. 哈尔滨工程大学学报, 2015, 36(5): 606-610.
[8]
YIN G, ZHANG Y, LI Z, et al. Detection of ferromagnetic target based on mobile magnetic gradient tensor system[J]. Journal of Magnetism & Magnetic Materials, 2016, 402: 1-7.
[9]
LIU R, WANG H. Detection and localization of improvised explosive devices based on 3-axis magnetic sensor array system[J]. Procedia Engineering, 2010, 7(12): 1-9.
[10]
万成彪, 潘孟春, 张琦, 等. 基于张量特征值和特征向量的磁性目标定位[J]. 吉林大学学报(工), 2017, 47(2): 655-660.
[11]
NARA T, SUZUKI S, ANDO S. A closed-form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3291-3293. DOI:10.1109/TMAG.2006.879151
[12]
SUI Y, LESLIE K, CLARK D. Multiple-order magnetic gradient tensors for localization of a magnetic dipole[J]. IEEE Magnetics Letters, 2017, 8: 1-5.
[13]
YIN G, ZHANG Y, FAN H, et al. Magnetic dipole localization based on magnetic gradient tensor data at a single point[J]. Journal of Applied Remote Sensing, 2014, 8(1): 1-18.
[14]
李光, 随阳轶, 刘丽敏, 等. 基于差分的磁偶极子单点张量定位方法[J]. 探测与控制学报, 2012, 34(5): 50-54.
[15]
FLOATER M, HORMANN K. Barycentric rational interpolation with no poles and high rates of approximation[J]. Numerische Mathematik, 2007, 107(2): 315-331. DOI:10.1007/s00211-007-0093-y
[16]
于振涛, 吕俊伟, 樊利恒, 等. 基于磁梯度张量的目标定位改进方法[J]. 系统工程与电子技术, 2014, 36(7): 1250-1254.