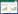文章信息
- 于涛, 王益博, 孙汉旭, 赵伟
- YU Tao, WANG Yibo, SUN Hanxu, ZHAO Wei
- 基于干扰观测器的球形移动机器人直线运动控制
- Linear motion control of a spherical mobile robot based on disturbance observer
- 中国测试, 2019, 45(9): 123-129
- CHINA MEASUREMENT & TEST, 2019, 45(9): 123-129
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018100021
-
文章历史
- 收稿日期: 2018-10-10
- 收到修改稿日期: 2018-11-23
2. 北京邮电大学自动化学院,北京 100876;
3. 北京印刷学院 信息工程学院,北京 102600
2. School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. School of Information Engineering, Beijing Institute of Graphic Communication, Beijing 102600, China
随着科技发展,移动机器人在不同的应用领域中发挥着日益重要的作用。球形移动机器人是一种具有球形外壳,并且通过滚动方式穿越地表环境的移动机器人。球形机器人移动时不需要借助任何可见的外部驱动,而且在工作空间中滚动时必须服从球——平面非完整约束。因此,球形移动机器人需要采用相对新颖的运动机构、巧妙复杂的动态分析方法和先进的控制算法[1-3]。球形外壳赋予球形移动机器人耐用、不会倾倒、与外界环境完全隔离的优点,在巡逻监视[4]、外星探测[5]、环境监测[6]、水下作业[7],甚至儿童教育[8]等方面球形移动机器人都有着广泛的应用。
球形移动机器人在工作空间内的滚动模式可以分为二维平面滚动模式和三维空间滚动模式。在二维平面滚动模式下,球形移动机器人进行典型的直线运动。从球形移动机器人直线运动控制方法的研究现状[9-14]来看,大部分现有方法[9-13]采用被控对象的标称模型[9-11]或标称模型的线性化模型[12-13]来设计控制器;但由于实际对象中不可避免地存在着很多无法用数学模型精确描述的不确定性,并且在设计控制系统时忽略了这些不确定性对控制性能的不良影响,导致基于上述方法[9-13]的控制器在实际中很难实现预期的性能品质。由此可知,球形移动机器人直线运动的鲁棒控制问题是目前该领域中亟待解决的重要问题之一。
针对球形移动机器人直线运动的鲁棒控制问题,本文设计一种基于滑模干扰观测器和双幂次趋近律的分层滑模控制器。具体而言,首先基于第一层滑动变量设计球壳和单摆子系统的滑模干扰观测器,然后提出一种改进的双幂次趋近律以使第二层滑动变量快速收敛于零,最后基于改进的双幂次趋近律和滑模干扰观测器设计连续的分层滑模控制器。并通过理论分析与仿真实验验证本文所设计的分层滑模控制器确保闭环控制系统的鲁棒稳定性。
1 球形机器人直线运动的动力学模型LGQ-I型三驱动球形机器人的三维模型如图1所示,其本体结构主要包括球壳、内框、单摆和直流电机。与BYQ-XII型三驱动球形机器人[14]相比,LGQ-I型三驱动球形机器人内框的尺寸和质量较小,而单摆的质量和摆杆的长度较大。因此,LGQ-I型三驱动球形机器人的单摆质量相对总体质量的占比很高,因而能够提供较大的偏心力矩,可以实现更迅速、更灵活的滚动运动。
|
| 图 1 LGQ-I型球形机器人的三维模型 |
当球壳内的长轴电机带动内框和单摆相对球壳转动时,球形机器人能够进行向前或向后的直线滚动。当轨道电机带动内框和单摆相对球壳转动时,球形机器人能够完成原地转向动作。当短轴电机带动单摆相对内框转动时,球形机器人能够在进行滚动运动时向左或向右转向。由此可见,LGQ-I型三驱动球形机器人具有一定的容错能力。当短轴电机或轨道电机出现故障时,球形机器人仍能实现全方位的滚动运动。
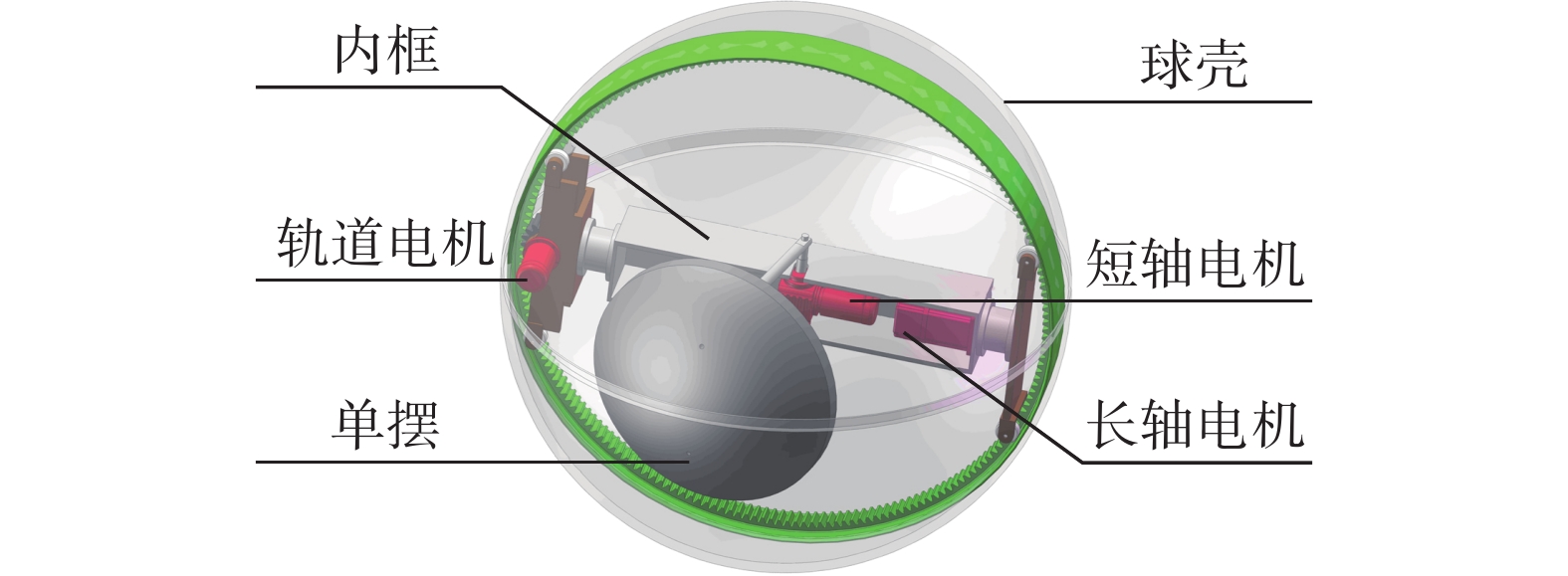
LGQ-I型三驱动球形机器人直线运动的简化模型如图2所示,在长轴电机输出力矩τ的作用下,球形机器人在XOZ平面内滚动。其中,球壳的质量为
|
| 图 2 LGQ-I型球形机器人直线运动的简化模型 |
基于拉格朗日法建立球形移动机器人直线运动的动力学模型,球形机器人系统的动能
| $U = \left( {\frac{1}{2}M + \frac{1}{3}{m_1}} \right){r^2}{\dot \theta ^2} + \frac{1}{2}J{\dot \phi ^2} + {m_3}rl\dot \theta \dot \phi \cos \phi $ | (1) |
其中
球形机器人系统的势能
| $V = - {m_3}gl\cos \phi $ | (2) |
利用含耗散函数的拉格朗日方程,由式(1)和式(2)可得球形移动机器人直线运动的运动方程为
| $ \left\{ {\begin{array}{*{20}{l}} \!\!{\left( {M + \frac{2}{3}{m_1}} \right){r^2}\ddot \theta + {m_3}rl\ddot \phi \cos \phi + \mu \left( {\dot \theta + \dot \phi } \right) - {m_3}rl{{\dot \phi }^2}\sin \phi = \tau }\\ \!\!{{m_3}rl\ddot \theta \cos \phi + \left( {{m_3}{l^2} + I} \right)\ddot \phi + \mu \left( {\dot \theta + \dot \phi } \right) + {m_3}gl\sin \phi = \tau } \end{array}} \right. $ | (3) |
其中
假设球壳在地面滚动时不打滑,则有如下关系式成立:
| $\begin{array}{*{20}{c}} {\dot \theta = {{\dot x}/ r}}&{}&{\ddot \theta = } \end{array}{{\ddot x} / r} $ | (4) |
将式(4)代入式(3),可得球形移动机器人直线运动的动力学模型为
| $ \bar {{M}}\left( {{q}} \right)\ddot {{q}} + {{N}}\left( {{{q}}, \dot {{q}}} \right) = {{F}}\tau $ | (5) |
式中:
| $ \begin{array}{*{20}{c}} &{\bar {{M}}\left( {{q}} \right) = \left[ {\begin{array}{*{20}{c}} {\frac{1}{3}\left( {5{m_1} + 3{m_2} + 3{m_3}} \right){r^2}}&{{m_3}{r^2}l\cos \phi }\\ {{m_3}rl\cos \phi }&{\left( {{m_3}{l^2} + I} \right)r} \end{array}} \right]} \\ &{{{q}} = \left[ {\begin{array}{*{20}{c}} x \\ \phi \end{array}} \right]} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{{N}}\left( {{{q}}, \dot {{q}}} \right) = \left[ {\begin{array}{*{20}{c}} {\mu \left( {\dot x + r\dot \phi } \right) - {m_3}{r^2}l{{\dot \phi }^2}\sin \phi } \\ {\mu \left( {\dot x + r\dot \phi } \right) + {m_3}grl\sin \phi } \end{array}} \right]}\\{{{F}} = \left[ {\begin{array}{*{20}{c}} r \\ r \end{array}} \right]} \end{array} $ |
由动力学模型式(5),可得直线运动时球形机器人系统的非完整约束条件为
| $ {g_1}\left( \phi \right)\ddot x + {g_2}\left( \phi \right)\ddot \phi - {g_3}\left( {\phi , \dot \phi } \right) = 0 $ | (6) |
式中:
| $ {g_1}\left( \phi \right) = \frac{1}{3}\left( {5{m_1} + 3{m_2} + 3{m_3}} \right)r - {m_3}l\cos \phi $ |
| $ {g_2}\left( \phi \right) = {m_3}rl\cos \phi - {m_3}{l^2} - I $ |
| ${g_3}\left( {\phi , \dot \phi } \right) = {m_3}rl{\dot \phi ^2}\sin \phi + {m_3}gl\sin \phi $ |
将球形移动机器人直线运动的动力学模型式(5)表示成如下形式:
| $\begin{array}{*{20}{c}} {\ddot x\left( t \right) = {f_1}\left( {\dot x, \phi , \dot \phi } \right) + {b_1}\left( \phi \right)\tau \left( t \right) + {d_1}\left( t \right)} \\ {\ddot \phi \left( t \right) = {f_2}\left( {\dot x, \phi , \dot \phi } \right) + {b_2}\left( \phi \right)\tau \left( t \right) + {d_2}\left( t \right)} \end{array}$ | (7) |
式中
| ${\left[ {\begin{array}{*{20}{c}} {{f_1}\left( {\dot x, \phi , \dot \phi } \right)}&{{f_2}\left( {\dot x, \phi , \dot \phi } \right)} \end{array}} \right]^{\rm T}} = - {\bar {{M}}^{ - 1}}\left( {{q}} \right){{N}}\left( {{{q}}, \dot {{q}}} \right)$ |
| ${\left[ {\begin{array}{*{20}{c}} {{b_1}\left( \phi \right)}&{{b_2}\left( \phi \right)} \end{array}} \right]^{\rm T}} = {\bar {{M}}^{ - 1}}\left( {{q}} \right){{F}}$ |
对于球形移动机器人,其直线运动的控制目标是:通过合理地设计控制律
| $ \begin{array}{*{20}{c}} {{s_1}\left( t \right) = {{\dot e}_x}\left( t \right) + {k_1}{e_x}\left( t \right)}&{{s_2}\left( t \right) = {{\dot e}_\phi }\left( t \right) + {k_2}{e_\phi }\left( t \right)} \end{array} $ | (8) |
式中
注1:由于球心的运动轨迹
由式(7)和式(8),进一步可得
| $ \begin{array}{*{20}{c}} {{{\dot s}_1}\left( t \right) = {h_1} + {b_1}\tau + {d_1}}&{{{\dot s}_2}\left( t \right) = {h_2} + {b_2}\tau + {d_2}} \end{array} $ | (9) |
式中
基于所设计的第一层各滑动变量
| ${s_3}\left( t \right) = {c_1} \cdot {s_1}\left( t \right) + {c_2} \cdot {s_2}\left( t \right)$ | (10) |
式中
对式(10)求导并由式(9),可得
| ${\dot s_3}\left( t \right) = {c_1}{\dot s_1} + {c_2}{\dot s_2} = {h_3} + {b_3}\tau + {c_1}{d_1} + {c_2}{d_2}$ | (11) |
式中
至此,球形移动机器人直线运动的控制目标转化为:在被控机器人系统式(7)存在未知扰动
首先采用滑模干扰观测器对未知扰动
定义辅助滑动变量
| $\begin{array}{*{20}{c}} {{\sigma _i}\left( t \right) = {s_i}\left( t \right) + {{\textit{z}}_i}\left( t \right),}&{{{\dot z}_i}\left( t \right) = - {h_i} - {b_i}\tau - {u_i},}&{i = 1, 2} \end{array}$ | (12) |
式中
由式(9)和式(12),可以得到
| $ {\dot \sigma _i}\left( t \right) = {\dot s_i} + {\dot {\textit{z}}_i} = {d_i} - {u_i} $ | (13) |
基于式(13)所示的辅助滑动变量
| $ \begin{array}{*{20}{c}} {{u_i}\left( t \right) = {\varepsilon _i}{\rm{sign}}\left( {{\sigma _i}} \right),}&{{\varepsilon _i} = {L_i} + {\rho _i}} \end{array} $ | (14) |
式中
设滑模干扰观测器i的注入项
实际中,采用干扰观测器注入项
| ${\gamma _i}{\dot {\bar u}_{{\rm eq}, i}}\left( t \right) + {\bar u_{{\rm eq}, i}}\left( t \right) = {u_i}\left( t \right)$ | (15) |
式中
在式(15)中,选取很小的滤波时间常数
| $\begin{array}{*{20}{c}} {{{\bar u}_{{\rm eq}, i}}\left( t \right) = {d_i}\left( t \right),}&{\forall t \geqslant {t_{{\rm r}, i}}} \end{array}$ | (16) |
记
| $\begin{array}{*{20}{c}} {{{\dot s}_3}\left( t \right) = {h_3} + {b_3}\tau + {c_1}{{\bar u}_{{\rm eq}1}} + {c_2}{{\bar u}_{{\rm eq}2}},}&{\forall t \geqslant {t_{{\rm r}3}}} \end{array}$ | (17) |
为使第二层滑动变量
基于文献[16]提出的双幂次趋近律,设计改进的双幂次趋近律为
| ${\dot s_3}\left( t \right) = - {\lambda _1}{\left| {{s_3}} \right|^\alpha }{\rm{sign}}\left( {{s_3}} \right) - {\lambda _2}{\left| {{s_3}} \right|^\beta }{\rm{sign}}\left( {{s_3}} \right) - {\lambda _3}{s_3}$ | (18) |
式中
注2:在改进的双幂次趋近律式(18)中,前2项为幂次趋近项,第3项为指数趋近项。如果不考虑控制增益
由式(17)和式(18),可得分层滑模控制器为
| $\tau \left( t \right) = - \dfrac{{{\lambda _1}{{\left| {{s_3}} \right|}^\alpha }{\rm{sign}}\left( {{s_3}} \right) + {\lambda _2}{{\left| {{s_3}} \right|}^\beta }{\rm{sign}}\left( {{s_3}} \right) + {\lambda _3}{s_3} + {h_3} + {c_1}{{\bar u}_{{\rm eq}1}} + {c_2}{{\bar u}_{{\rm eq}2}}}}{{{b_3}}}$ | (19) |
分析1:对于式(7)所示的球形机器人系统,按式(8)和式(10)设计各层滑动变量,并按式(12)和式(14)设计滑模干扰观测器,如果采用式(19)所示的分层滑模控制器,那么第二层滑动变量
证明:将控制律式(19)代入式(11),可以得到
| $\begin{split} {{\dot s}_3}\left( t \right) = &- {\lambda _1}{\left| {{s_3}} \right|^\alpha }{\rm{sign}}\left( {{s_3}} \right) - {\lambda _2}{\left| {{s_3}} \right|^\beta }{\rm{sign}}\left( {{s_3}} \right) - \\ &{\lambda _3}{s_3} + {c_1}\left( {{d_1} - {{\bar u}_{{\rm eq}1}}} \right) + {c_2}\left( {{d_2} - {{\bar u}_{{\rm eq}2}}} \right) \\ \end{split} $ | (20) |
为便于分析,将第二层滑动变量
第2阶段是第二层滑动变量
| $ \begin{array}{*{20}{c}} {{{\dot s}_3} \cdot {s_3} = - {\lambda _1}{{\left| {{s_3}} \right|}^{\alpha + 1}} - {\lambda _2}{{\left| {{s_3}} \right|}^{\beta + 1}} - {\lambda _3}s_3^2 < 0,}&{\forall t \geqslant {t_{{\rm r}3}}} \end{array} $ | (21) |
由式(21)可见,第二层滑动变量
考虑到
| ${t_{{\rm r}5}} \leqslant \frac{{1 - {{\left| {{s_3}\left( {{t_{{\rm r}3}}} \right)} \right|}^{1 - \alpha }}}}{{{\lambda _1}\left( {\alpha - 1} \right)}} + \frac{1}{{{\lambda _2}\left( {1 - \beta } \right)}} < \frac{1}{{{\lambda _1}\left( {\alpha - 1} \right)}} + \frac{1}{{{\lambda _2}\left( {1 - \beta } \right)}}$ | (22) |
由式(22),进一步可得第二层滑动变量
| $\begin{split} {t_{{\rm r}4}} =& {t_{{\rm r}3}} + {t_{{\rm r}5}} < \max \left( {\frac{{\left| {{\sigma _1}\left( 0 \right)} \right|}}{{{\rho _1}}}, \frac{{\left| {{\sigma _2}\left( 0 \right)} \right|}}{{{\rho _2}}}} \right) +\\& \frac{1}{{{\lambda _1}\left( {\alpha - 1} \right)}} + \frac{1}{{{\lambda _2}\left( {1 - \beta } \right)}} \\ \end{split} $ | (23) |
注3:在对第2阶段的时间
分析2:对于式(7)所示的球形机器人系统,按式(8)和式(10)设计各层滑动变量,并按式(12)和式(14)设计滑模干扰观测器,如果采用式(19)所示的分层滑模控制器,那么第一层滑动变量
对于按式(8)设计的第一层各滑动变量,由文献[18]定理4.2的证明可知,在分层滑模控制器式(19)的作用下,滑动变量
为验证本文提出的控制方法的有效性,利用Matlab/Simulink仿真环境进行球形移动机器人直线运动的速度控制实验。LGQ-I型三驱动球形机器人的各参数分别为:
设球形移动机器人的初始状态为:
为检验本文提出的控制方法的控制性能和鲁棒性,假设实际球形机器人带有10%的参数不确定性,在此基础上与文献[14]提出的控制方法进行对比分析。将文献[14]提出的控制方法应用于直线运动的速度控制问题时,需要将球形移动机器人的期望轨迹
| $\begin{array}{*{20}{c}} {{y_{\rm{d}}} = {x_{\rm ref}}\left( t \right)}&{}&{{\tau _{{\rm{eq}}1}} = - \frac{{{g_1} + {\lambda _1}{{\dot e}_y}}}{{{b_1}}}} \end{array}$ | (24) |
为确保两种控制方法均能提供最优的控制性能,对基于两种控制方法的控制器各参数进行充分整定。在进行仿真对比时,基于本文方法的控制器各参数分别为:
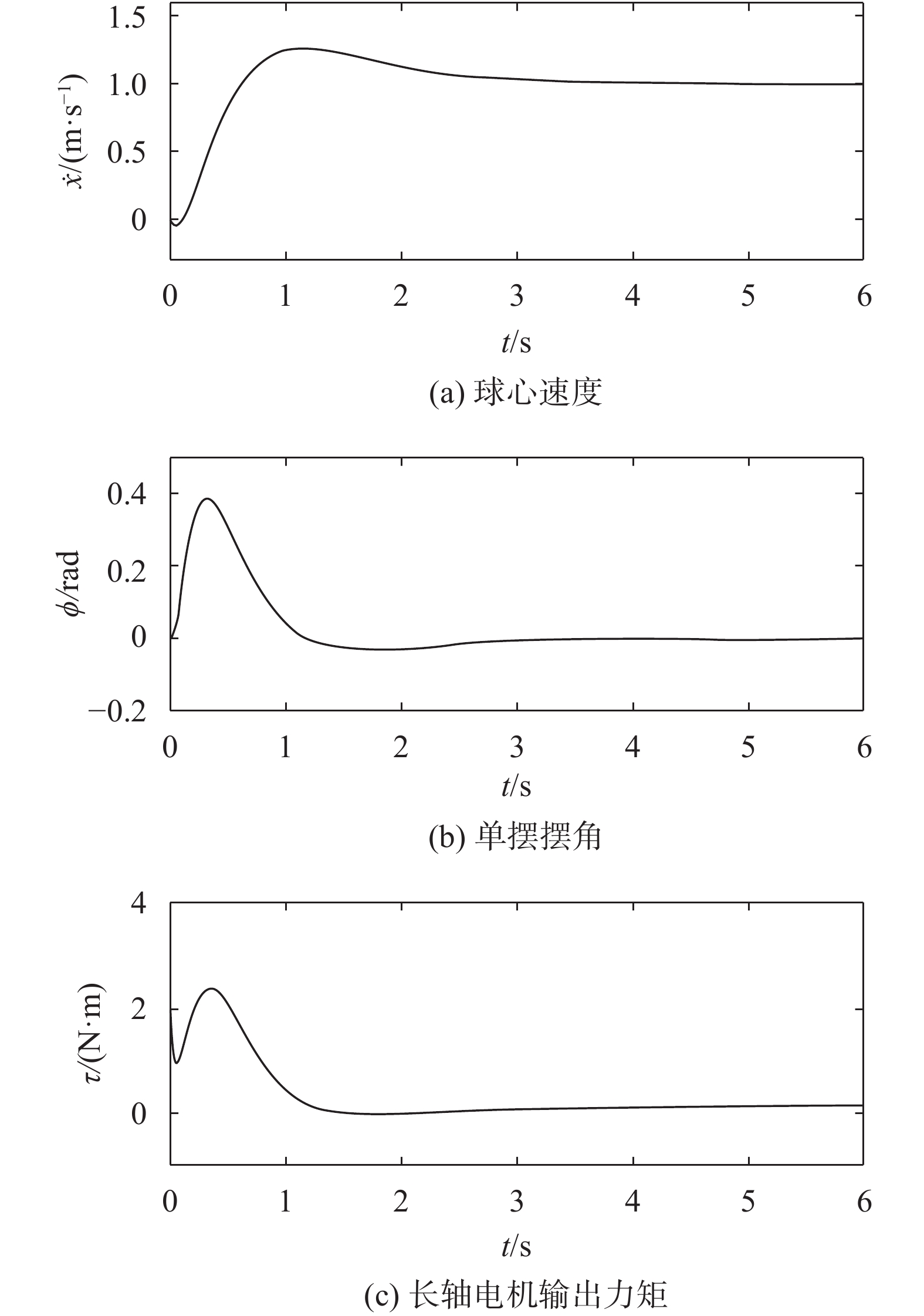
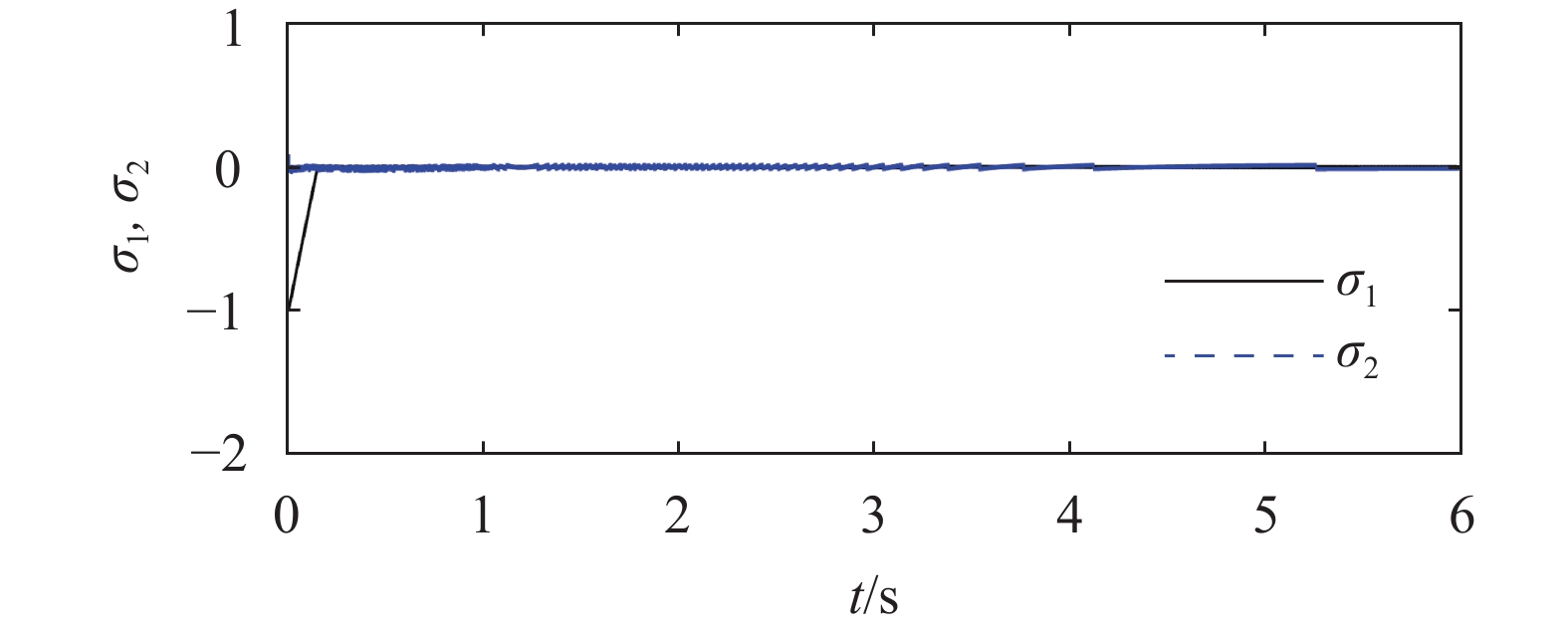
基于本文方法的控制器的控制效果如图3至图5所示。图3为球心速度、单摆摆角和长轴电机输出力矩的变化曲线,可见在基于本文方法的连续分层滑模控制器式(19)作用下,球心速度和单摆摆角分别于3.122 s和3.039 s收敛至各自的期望值。仿真实验结果表明,本文方法能够有效实现球形移动机器人直线运动的连续鲁棒控制。图4和图5分别为各辅助滑动变量和各层滑动变量的变化曲线,可见各滑动变量均能快速地收敛于零。具体而言,由图4可见辅助滑动变量的整体收敛时间为
|
| 图 3 基于本文方法的控制器的控制效果 |

|
| 图 5 各层滑动变量的变化曲线 |
|
| 图 4 各辅助滑动变量的变化曲线 |
基于文献[14]方法的控制器的控制效果如图6所示。可以看出,在基于文献[14]方法的控制器作用下,球心速度和单摆摆角分别于3.48 s和2.891 s收敛至各自的期望值。需要指出的是,虽然两种控制方法均能实现被控球形机器人系统的连续鲁棒控制,但本文方法采用的是连续的控制律,而文献[14]方法采用的是连续化的控制律,这也是两种控制方法的重要区别之一。此外,由仿真实验结果可见:当球心速度趋于稳定后,长轴电机仍需提供一定的平衡力矩以补偿内框与球壳之间的粘滞摩擦力。由动力学模型式(5)可以推得,长轴电机输出的平衡力矩为
为评价球形机器人速度控制器的控制性能,分别定义球心速度平均跟踪误差
| $\begin{array}{*{20}{c}} {E\left( {\dot x} \right) = \frac{1}{n} \cdot \displaystyle\sum\limits_{i = 1}^n {\left| {{{\dot e}_x}\left( {{t_i}} \right)} \right|} }&{}&{E\left( \phi \right) = \frac{1}{n} \cdot \displaystyle\sum\limits_{i = 1}^n {\left| {{e_\phi }\left( {{t_i}} \right)} \right|} } \end{array}$ | (25) |
式中
由式(25)可以分别求得在基于本文方法的控制器作用下和基于文献[14]方法的控制器作用下,球心速度平均跟踪误差
由表可以看出,相较于基于文献[14]方法的控制器,在基于本文方法的控制器作用下,球心速度平均跟踪误差
本文探讨了带有未知扰动的球形移动机器人的直线运动控制问题,提出一种基于滑模干扰观测器和改进的双幂次趋近律的分层滑模控制方法。本文提出的控制方法利用干扰观测器注入项的等效控制对被控机器人系统的未知扰动进行在线估计,并且采用基于干扰观测器注入项的等效控制和改进的双幂次趋近律的连续分层滑模控制器实现被控机器人系统的快速稳定。从理论上证明了各辅助滑动变量和各层滑动变量的收敛性,仿真实验结果表明本文设计的分层滑模控制器能够提供良好的控制性能和鲁棒性。
| [1] |
ARMOUR R H, VINCENT J F V. Rolling in nature and robotics: a review[J].
Journal of Bionic Engineering, 2006, 3(4): 195-208.
DOI:10.1016/S1672-6529(07)60003-1 |
| [2] |
CROSSLEY V A. A literature review of the design of spherical rolling robots[R]. Pittsburgh, Carnegie Mellon University, 2006.
|
| [3] |
CHASE D, PANDYA A. A review of active mechanical driving principles of spherical robots[J].
Robotics, 2012, 1(1): 3-23.
DOI:10.3390/robotics1010003 |
| [4] |
WU F, VIBHUTE A, SOH G S, et al. A compact magnetic field-based obstacle detection and avoidance system for miniature spherical robots[J].
Sensors, 2017, 17(6): 1-20.
DOI:10.1109/JSEN.2017.2656005 |
| [5] |
HOGAN F R, FORBES J R, BARFOOT T D. Rolling stability of a power-generating tumbleweed rover[J].
Journal of Spacecraft and Rockets, 2015, 51(6): 1895-1906.
|
| [6] |
HERNANDEZ J D, BARRIENTOS J, CERRO J D, et al. Moisture measurement in crops using spherical robots[J].
Industrial Robot: An International Journal, 2013, 40(1): 59-66.
DOI:10.1108/01439911311294255 |
| [7] |
LI Y, YANG M, SUN H, et al. A novel amphibious spherical robot equipped with flywheel, pendulum, and propeller[J].
Journal of Intelligent and Robotic Systems, 2017, 2: 1-17.
|
| [8] |
MICHAUD F, LAPLANTE J F, LAROUCHE H, et al. Autonomous spherical mobile robot for child-development studies[J].
IEEE Transactions on Systems, Man, and Cybernetics, 2005, 35(4): 1-10.
|
| [9] |
MADHUSHANI T W U, MAITHRIPALA D H S, BERG J M. Feedback regularization and geometric PID control for trajectory tracking of mechanical systems: hoop robots on an inclined plane[C]//American Control Conference, 2017.
|
| [10] |
ZHAN Q, CHI X, XI X. Linear motion control of an underactuated spherical mobile robot[J].
Applied Mechanics and Materials, 2014, 644-650: 351-355.
DOI:10.4028/www.scientific.net/AMM.644-650.351 |
| [11] |
IVANOVA T B, PIVOVAROVA E N. Dynamics and control of a spherical robot with an axisymmetric pendulum actuator[J].
Physics, 2015, 9(3): 507-520.
|
| [12] |
YE P, SUN H, QIU Z, et al. Design and motion control of a spherical robot with stereovision[C]//IEEE Conference on Industrial Electronics and Applications, 2016.
|
| [13] |
YUE M, LIU B. Disturbance adaptive control for an underactuated spherical robot based on hierarchical sliding-mode technology[C]// Chinese Control Conference, 2012.
|
| [14] |
于涛, 孙汉旭, 赵伟, 等. 基于自适应分级滑模控制的球形机器人定位控制[J].
中国测试, 2018, 44(5): 97-102.
DOI:10.11857/j.issn.1674-5124.2018.05.019 |
| [15] |
UTKIN V, GULDNER J, SHI J M. Sliding mode control in electro-mechanical systems[M]. Boca Raton: CRC, 2009: 216.
|
| [16] |
梅红, 王勇. 快速收敛的机器人滑模变结构控制[J].
信息与控制, 2009, 38(5): 552-557.
|
| [17] |
张合新, 范金锁, 孟飞, 等. 一种新型滑模控制双幂次趋近律[J].
控制与决策, 2013, 28(2): 289-293.
|
| [18] |
QIAN D, YI J. Hierarchical sliding mode control for under-actuated cranes: design, analysis and simulation[M]. Berlin: Springer-Verlag , 2016.
|
 2019, Vol. 45
2019, Vol. 45