文章信息
- 王见, 王作学, 张波
- WANG Jian, WANG Zuoxue, ZHANG Bo
- 振动系统PID零极点配置理论
- PID poles and zeros assignment theory in vibration system
- 中国测试, 2019, 45(1): 121-127
- CHINA MEASUREMENT & TEST, 2019, 45(1): 121-127
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018030012
-
文章历史
- 收稿日期: 2018-03-09
- 收到修改稿日期: 2018-04-16
2. 中国石油西南油气田分公司(重庆气矿工艺研究所),重庆 401147
2. Petro China Southwest Oil and Gasfield Company (Chongqing Gas District), Chongqing 401147, China
由于系统的振动特性由其极点及零点值决定,因此系统的零极点特征值赋值问题是系统主动振动控制的中心研究问题之一。在传统主动振动控制问题中常通过有限元法分析系统的理论模型获得系统的质量、阻尼和刚度矩阵,进而求得极点配置问题最优解[1-4]。鉴于有限元法存在难以获得实际结构精确阻尼模型的缺陷,近年来Mottershead等[5]开发了基于柔度法的线性系统主动振动控制方法以精确分配系统极点和零点到指定数值。该方法的一个重要优点是振动控制过程完全基于模态测试数据,无需通过有限元法获取系统的精确质量、阻尼和刚度矩阵。Ghandchi Tehrani 等[6]采用输入反馈算法在使非重要极点不可控或不可观测的情况下,实现了将系统部分极点分配到预定值而保持其他极点不变的效果。Mottershead等[7]展示了输入反馈控制零极点配置算法具有可实现传感器与作动器并置的优点。除了以上研究,许多其他类型的反馈控制也被引入到了主动振动控制中。如Zhang等[8]提出了将加速度反馈与位置反馈应用到无阻尼系统中实现部分极点配置;H. Ouyang[9]研究了将加速度和速度反馈用于主动振动控制。从这些研究结果可以看出,目前主动振动控制零极点配置算法多使用加速度、速度和位移反馈及其各种组合来实现。然而,当系统引入加速度反馈时,振动系统不可避免地将可能变成奇异系统而导致动柔度法不可使用,为此本文引入了积分控制以避免该情况的发生;同时在保留速度控制及加速度控制基础上研究了基于动柔度法的PID输入反馈主动振动控制,保证了控制系统的非奇异性,拓展了主动振动控制的适用系统范围,补充了动柔度法在微分控制方面的研究。另外结合本零极点配置算法,本文提出系统可配置极点数目、最佳传感器及反馈增益配置方法的概念及其相关算法。
1 PID输入反馈控制极点分配理论 1.1 基于动柔度法的极点分配多自由度线性系统自由振动方程[4]一般表示为
| ${{M\ddot x}}\left( t \right) + {{C\dot x}}\left( t \right) + {{Kx}}\left( t \right) = {\bf{0}}$ | (1) |
其中
对上述线性系统实施单输入PID控制,则控制方程如下:
| ${{M\ddot x}} + {{C\dot x}} + {{Kx}} = {{b}}u\left( t \right)$ | (2) |
其中
| $u\left( t \right) = {{g}}_1^{\rm{T}}{{x}}\left( t \right) + {{g}}_2^{\rm{T}}\int\limits_0^t {{{x}}\left( \tau \right){\rm{d}}\tau } + {{g}}_3^{\rm{T}}{{\dot x}}\left( t \right)$ | (3) |
式中
对式(2)进行拉普拉斯变换,得:
| $\left[ {{{M}}{s^2} + {{C}}s + {{K}}} \right]{{x}}\left( s \right) = {{b}}\left( {{{g}}_1^{\rm{T}} + \frac{{{{g}}_2^{\rm{T}}}}{s} + s{{g}}_3^{\rm{T}}} \right){{x}}\left( s \right)$ | (4) |
移项得:
| $\left[ {{{M}}{s^2} + {{C}}s + {{K}} - {{b}}\left( {{{g}}_1^{\rm{T}} + \frac{{{{g}}_2^{\rm{T}}}}{s} + s{{g}}_3^{\rm{T}}} \right)} \right]{{x}}\left( s \right) = {\bf{0}}$ | (5) |
从式(5)可知:系统刚度矩阵的最高阶
对式(5),利用Sherman-Morrison公式得到闭环系统柔度矩阵为
| ${{\hat H}}(s) = {{H}}(s) + \frac{{{{H}}(s){{b}}{{\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{s} + s{{{g}}_3}} \right)}^{\rm{T}} }{{H}}(s)}}{{1 - {{\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{s} + s{{{g}}_3}} \right)}^{\rm{T}} }{{H}}(s){{b}}}}$ | (6) |
其中
| $p(s) = 1 - {\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{s} + s{{{g}}_3}} \right)^{\rm{T}} }{{H}}(s){{b}}$ | (7) |
闭环系统的极点即为下式的根:
| $p(s) = 0$ | (8) |
因此,将闭环系统极点分配到设定值
| $p({\mu _i}) = 0$ | (9) |
求增益向量
令矩阵
| $1 - {\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{s} + s{{{g}}_3}} \right)^{\rm{T}} }\frac{{{{A}}(s)}}{{d(s)}}{{b}} = 0$ | (10) |
由于对
| $sd(s) - {\left( {s{{{g}}_1} + {{{g}}_2} + {s^2}{{{g}}_3}} \right)^{\rm{T}} }{{A}}(s){{b}} = 0$ | (11) |
令:
| $q(s) = {\left( {s{{{g}}_1} + {{{g}}_2} + {s^2}{{{g}}_3}} \right)^{\rm{T}} }{{A}}(s){{b}}$ | (12) |
则
实际上闭环系统引入积分控制后将不再是常规系统,而成为广义系统。则
由式(7),
| ${{Gg}} = {{\gamma }}$ | (13) |
其中:
| $\begin{gathered} {{G}} = \left[ {\begin{array}{*{20}{c}} {{\bf{\psi }}_1^{\rm{T}} }&{\frac{{{\bf{\psi }}_1^{\rm{T}} }}{{{\mu _1}}}}&{{\mu _1}{\bf{\psi }}_1^{\rm{T}} } \\ {{\bf{\psi }}_2^{\rm{T}} }&{\frac{{{\bf{\psi }}_2^{\rm{T}} }}{{{\mu _2}}}}&{{\mu _2}{\bf{\psi }}_2^{\rm{T}} } \\ \vdots & \vdots & \vdots \\ {{\bf{\psi }}_N^{\rm{T}} }&{\frac{{{\bf{\psi }}_N^{\rm{T}} }}{{{\mu _N}}}}&{{\mu _N}{\bf{\psi }}_N^{\rm{T}} } \end{array}} \right],{{\bf{\psi }}_i} = {{H}}({\mu _i}){{b}}, \hfill \\ {{{g}}^{\rm{T}} } = \left[ {\begin{array}{*{20}{c}} {{{g}}_1^{\rm{T}} }&{{{g}}_2^{\rm{T}} }&{{{g}}_3^{\rm{T}} } \end{array}} \right],{{{\gamma }}^{\rm{T}} } = \left[ {\begin{array}{*{20}{c}} 1& \cdots &1 \end{array}} \right], \end{gathered} $ |
即针对式(2)所提出的极点配置问题可由式(13)进行求解。其中式(13)的一种求解实现形式为
| ${{{g}}^ * } = {{{G}}^ + }{{\gamma }}$ | (15) |
考虑到对实际系统控制时附加质量要求的限制,用于测量系统运动参数的传感器数量应尽可能少。因此
当预设极点序列
由式(5)知闭环柔度矩阵
| ${{\hat H}}(s) = {{\varOmega }} {(s)^{ - 1}}$ | (18) |
其中,
| ${{\varOmega }}(s) = {{M}}{s^2} + {{C}}s + {{K}} - {{b}}\left( {{{g}}_1^{\rm{T}} + \frac{{{{g}}_2^{\rm{T}}}}{s} + s{{g}}_3^{\rm{T}}} \right)$ | (19) |
验证确定的某种
由此,可以归纳验证过程为:确定特定的输入反馈方法
由于零点分配在振动控制中具有重要意义[5-7],因此本文给出了闭环系统零点分配方法。
由表达式(6)可知,通过选择合适的增益向量
闭环系统(i,j)处的柔度表达式为
| ${\hat H_{i{\rm{ }}j}}(s) = {{e}}_i^{\rm{T}} \left( {{{H}}(s) + \frac{{{{H}}(s){{b}}{{\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{s} + s{{{g}}_3}} \right)}^{\rm{T}} }{{H}}(s)}}{{1 - {{\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{s} + s{{{g}}_3}} \right)}^{\rm{T}} }{{H}}(s){{b}}}}} \right){{{e}}_j}$ | (20) |
其中
因此将闭环系统柔度
| $\begin{split} &{{e}}_i^{\rm{T}} \left\{ {\left[ {1 - {{\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{{{\xi _k}}} + {\xi _k}{{{g}}_3}} \right)}^{\rm{T}} }{{H}}({\xi _k}){{b}}} \right]{{H}}({\xi _k})} \right. + \\ &\quad \left. {{{H}}({\xi _k}){{b}}{{\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{{{\xi _k}}} + {\xi _k}{{{g}}_3}} \right)}^{\rm{T}} }{{H}}({\xi _k})} \right\}{{{e}}_j} = 0 \end{split} $ | (21) |
求解
将式(18)变形得:
| $\begin{split} & \left[ {{{\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{{{\xi _k}}} + {\xi _k}{{{g}}_3}} \right)}^{\rm{T}} }{{H}}({\xi _k}){{b}}} \right]{{e}}_i^{\rm{T}} {{H}}({\xi _k}){{{e}}_j} - \\ & {{e}}_i^{\rm{T}} {{H}}({\xi _k}){{b}}{\left( {{{{g}}_1} + } {\frac{{{{{g}}_2}}}{{{\xi _k}}} + {\xi _k}{{{g}}_3}} \right)^{\rm{T}} }{{H}}({\xi _k}){{{e}}_j} = {{e}}_i^{\rm{T}} {{H}}({\xi _k}){{{e}}_j} \end{split} $ | (22) |
即:
| $\begin{split} &{H_{i{\rm{ }}j}}({\xi _k})\left[ {{{\left( {{{{g}}_1} + \frac{{{{{g}}_2}}}{{{\xi _k}}} + {\xi _k}{{{g}}_3}} \right)}^{\rm{T}} }{{H}}({\xi _k}){{b}}} \right] - \\ &{{e}}_i^{\rm{T}}{{{H}}({\xi _k}){{b}}\left( {{{{g}}_1} + } {\frac{{{{{g}}_2}}}{{{\xi _k}}} + {\xi _k}{{{g}}_3}} \right)^{\rm{T}} }{{H}}({\xi _k}){{{e}}_j} = {H_{i{\rm{ }}j}}({\xi _k}) \end{split} $ | (23) |
其中
| ${{{t}}_k} = {H_{i{\rm{ }}j}}({\xi _k}){{H}}({\xi _k}){{b}} - {{e}}_i^{\rm{T}} {{H}}({\xi _k}){{bH}}({\xi _k}){{{e}}_j}$ | (24) |
故当将闭环系统零点分配为
| $\left[ {\begin{array}{*{20}{c}} {{{t}}_1^{\rm{T}} }&{\displaystyle\frac{{{{t}}_1^{\rm{T}} }}{{{\xi _1}}}}&{{\xi _1}{{t}}_1^{\rm{T}} } \\ {{{t}}_2^{\rm{T}} }&{\displaystyle\frac{{{{t}}_2^{\rm{T}} }}{{{\xi _2}}}}&{{\xi _2}{{t}}_2^{\rm{T}} } \\ \vdots & \vdots & \vdots \\ {{{t}}_r^{\rm{T}} }&{\displaystyle\frac{{{{t}}_r^{\rm{T}} }}{{{\xi _r}}}}&{{\xi _r}{{t}}_r^{\rm{T}} } \end{array}} \right]\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{g}}_1}} \\ {{{{g}}_2}} \\ \end{array}} \\ {{{{g}}_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{H_{i{\rm{ }}j}}({\xi _1})} \\ {{H_{i{\rm{ }}j}}({\xi _2})} \\ \vdots \\ {{H_{i{\rm{ }}j}}({\xi _r})} \end{array}} \right)$ | (25) |
其中,令:
| ${{T}} = \left[ {\begin{array}{*{20}{c}} {{{t}}_1^{\rm{T}} }&{\displaystyle\frac{{{{t}}_1^{\rm{T}} }}{{{\xi _1}}}}&{{\xi _1}{{t}}_1^{\rm{T}} } \\ {{{t}}_2^{\rm{T}} }&{\displaystyle\frac{{{{t}}_2^{\rm{T}} }}{{{\xi _2}}}}&{{\xi _2}{{t}}_2^{\rm{T}} } \\ \vdots & \vdots & \vdots \\ {{{t}}_r^{\rm{T}} }&{\displaystyle\frac{{{{t}}_r^{\rm{T}} }}{{{\xi _r}}}}&{{\xi _r}{{t}}_r^{\rm{T}} } \end{array}} \right]$ | (26) |
由式(22)可知当预设零点
工程应用中,有时需要同时对零点与极点进行分配,结合式(13)与式(22)可对闭环系统同时进行零极点分配,此时应注意零极点分配总数目
为验证上述理论,考虑如下三自由度阻尼-质量-弹簧系统进行数值仿真:
| $\begin{aligned}&{{M = }}\left[ {\begin{array}{*{20}{c}} 2&{}&{} \\ {}&2&{} \\ {}&{}&3 \end{array}} \right]\quad{{C}} = \left[ {\begin{array}{*{20}{c}} {2.5}&{ - 2}&0 \\ { - 2}&3&{ - 1} \\ 0&{ - 1}&1 \end{array}} \right]\\&{{K}} = \left[ {\begin{array}{*{20}{c}} {10}&{ - 3}&{ - 4} \\ { - 3}&3&0 \\ { - 4}&0&4 \end{array}} \right] \end{aligned} $ |
则可得系统开环系统极点:–0.030 5±0.589 4i,– 0.850 3±1.011 9i,–0.660 9±2.120 0i。
现用本文所提出的理论对系统极点进行配置,以改善系统闭环响应。设
由式(15)可得
| $\begin{gathered} {{{g}}_1} = {\left[ {\begin{array}{*{20}{c}} { - 38.181\;7}&{ - 6.781\;0}&{11.376\;5} \end{array}} \right]^{\rm{T}} } \hfill \\ {{{g}}_2} = {\left[ {\begin{array}{*{20}{c}} {3.739\;6}&{ - 14.448\;7}&{2.420\;3} \end{array}} \right]^{\rm{T}} } \hfill \\ {{{g}}_3} = {\left[ {\begin{array}{*{20}{c}} { - 4.135\;7}&{ - 4.590\;4}&{ - 10.660\;8} \end{array}} \right]^{\rm{T}} } \hfill \\ \end{gathered} $ |
同时经1.4中验证方法验证知:系统可配置闭环系统极点可被
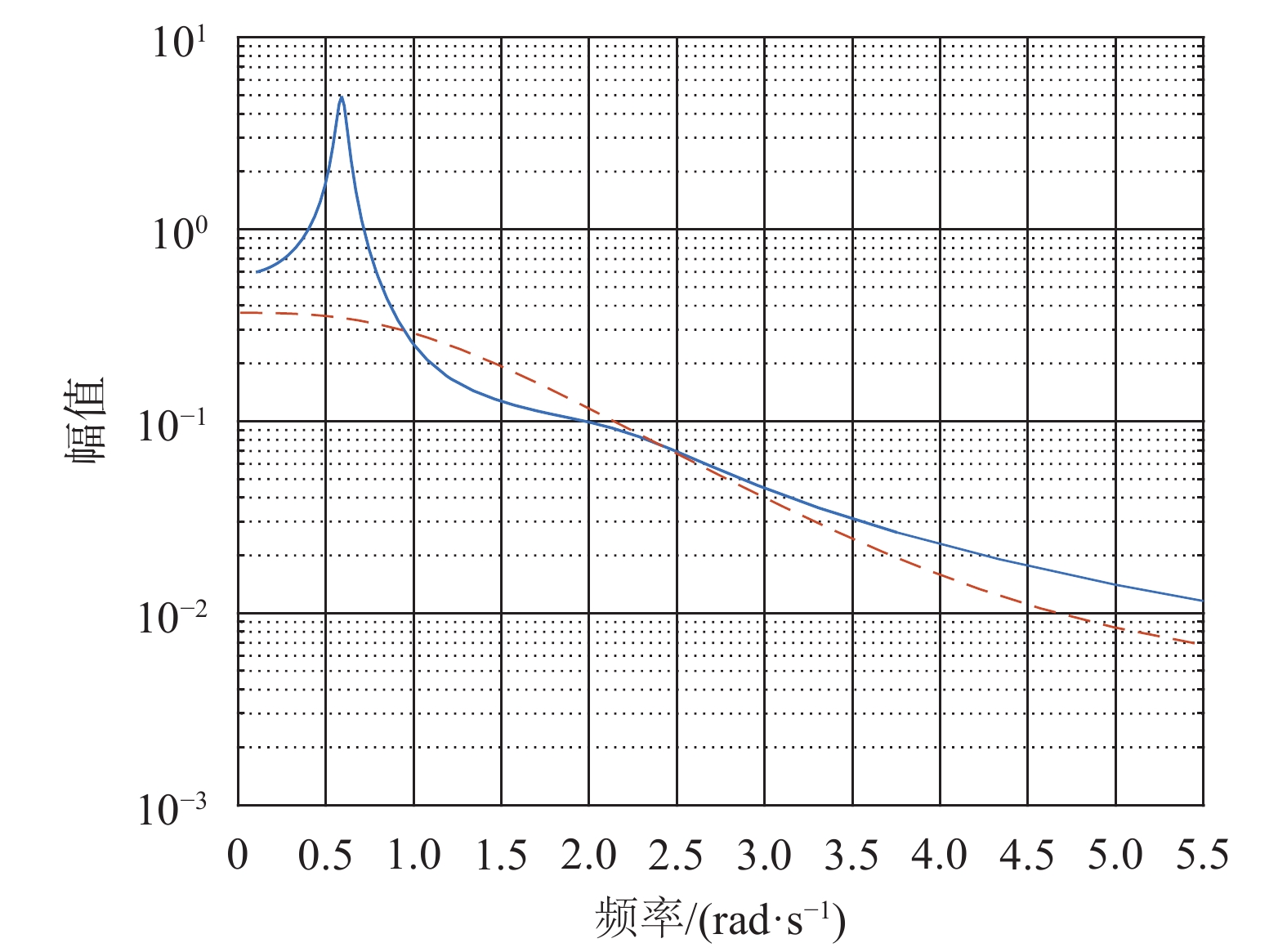
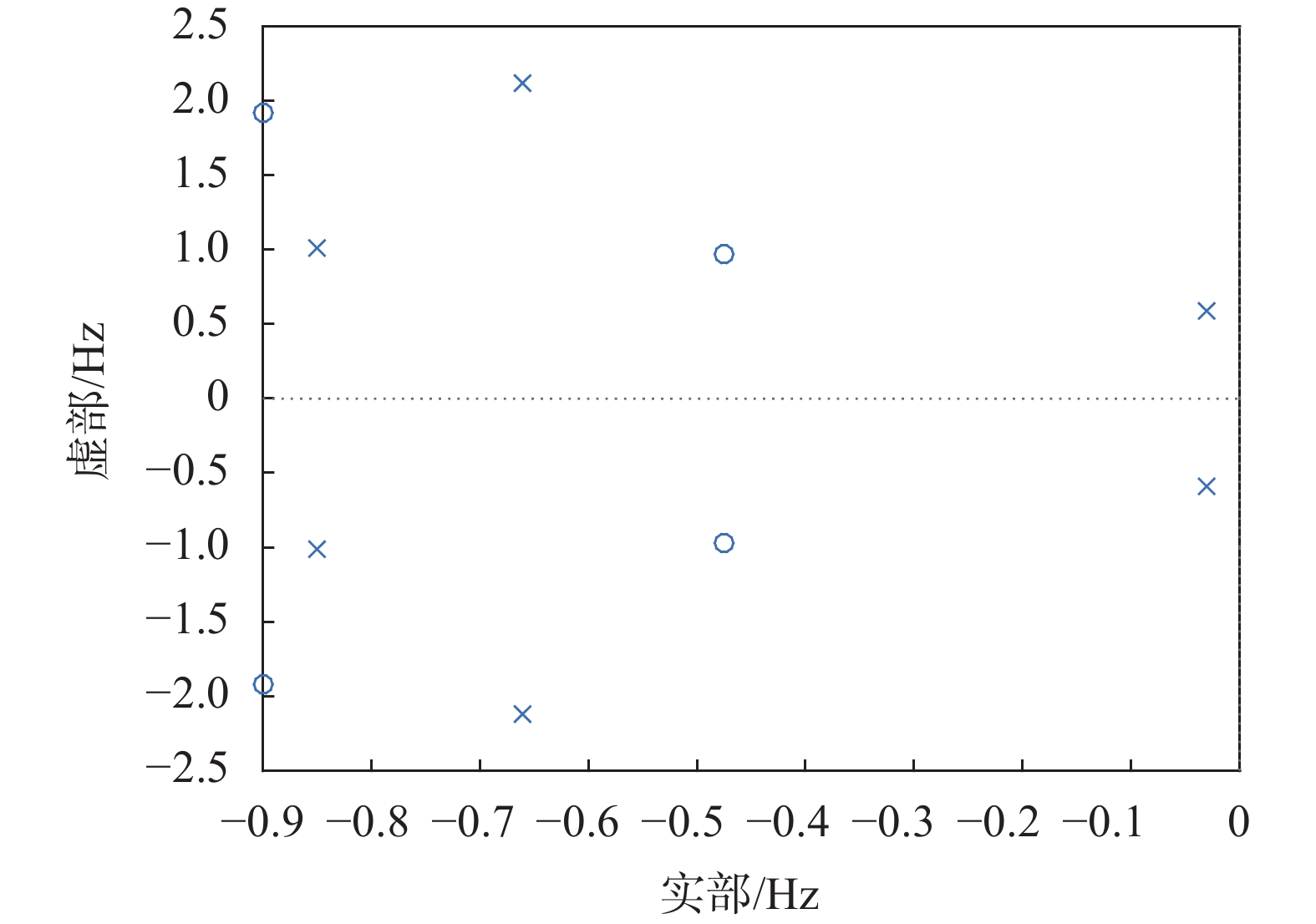
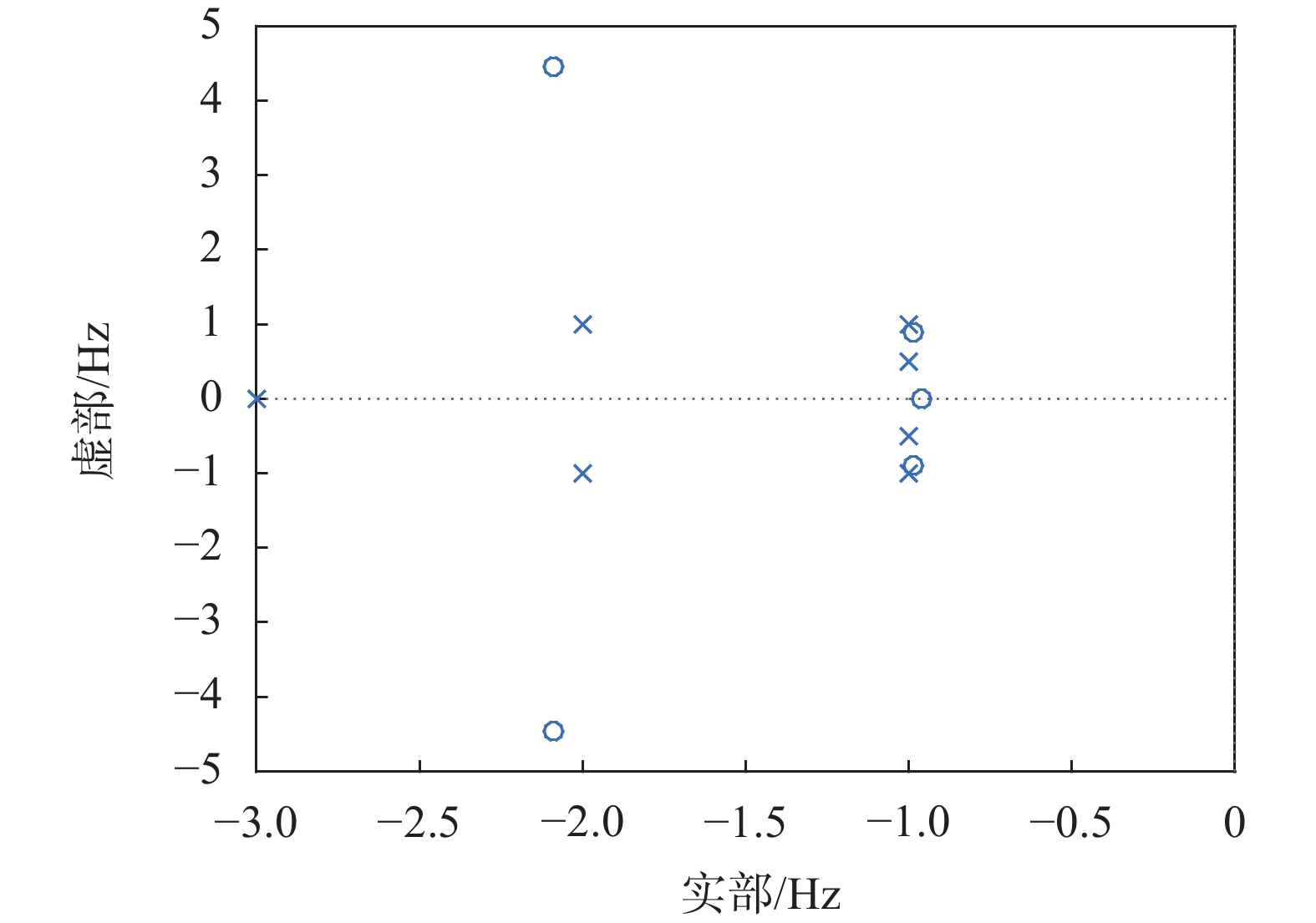
为突出极点分配效果,给出原系统及修改后系统H33处的频率响应曲线、零极点分布图及奈奎斯特图如图1~图5所示。由图3及图2对比可知系统极点被分配到了预设位置。且由于积分反馈的引入,修改后系统增加了一个闭环极点。在工程实际中此极点的引入增加了配置闭环系统极点值的灵活性。结合图1、图4、图5可看出系统极点重分配后闭环系统的特征频率增大,阻尼增大,系统稳定性增强,系统固有特性得到改变。
|
| 图 1 原系统H33(实线)及修改系统H33(虚线)频率响应 Fig. 1 The original system H33(solid line) and modification system H33(dotted line) frequency response |
|
| 图 2 原系统H33零极点分布 Fig. 2 The original system H33 zero-pole map |
|
| 图 3 修改系统H33零极点分布 Fig. 3 The modification system H33 pole-zero map |

|
| 图 4 原系统H33奈奎斯特曲线 Fig. 4 The original system H33Nyquist curve |

|
| 图 5 修改系统H33奈奎斯特曲线 Fig. 5 The modification system H33Nyquist curve |
3.2 传感器合理配置数值实例
在3.1节极点分配的基础上,可利用1.3节末尾的方法来寻找本例的最少传感器布置方案,并用1.4节的方法进行验证。表1给出了可将3.1节所示系统极点分配至
| 方法 | G 中零向量所替换的列 |
| W1 | {1},{2},{3 },{4},{5},{6},{7},{8},{9} |
| W2 | {1,2},{1,3},{2,3},{1,4},{2,4},{3,4},{1,5},{2,5},{3,5},{4,5},{1,6},{2,6},{3,6},{4,6},{5,6},{1,7},{2,7},{3,7},{4,7},{5,7},{6,7},{1,8},{2,8},{3,8},{4,8},{5,8},{6,8},{7,8},{1,9},{2,9},{3,9},{4,9},{5,9},{6,9},{7,9},{8,9} |
| 方法 | 控制增益 |
| W1 | g1=[ 0 −64.649 9 33.375 5] T g2=[ 55.159 0 −68.253 5 18.766] T g3=[ 5.111 5 −31.213 1 15.402 3] T |
| W2 | g1=[ 0 0 −23.193 1] T g2=[ 301.636 7 −56.131 7 −191.435 6] T g3=[ 37.436 5 9.193 1 −93.694 4] T |
进一步对系统作缺少极点分配计算(表3所示分配缺陷极点数为
| 预设极点序列 | 反馈增益向量 | 实际极点 |
|
|
g1=[ −8.845 5 0.998 7 11.564 6] T g2=[ 4.907 5 1.194 8 −1.561 9] T g3=[ −13.096 3 1.724 8 5.581 9] T |
|
3.3 零点分配数值实例
基于3.1中三自由度阻尼-质量-弹簧系统,设
由式(22)可得此时
| $\begin{gathered} {{{g}}_1} = {\left[ {\begin{array}{*{20}{c}} {1.962\;3}&{ - 3.044\;8}&0 \end{array}} \right]^{\rm{T}} } \\ {{{g}}_2} = {\left[ {\begin{array}{*{20}{c}} { - 1.321\;5}&{ - 0.491\;2}&0 \end{array}} \right]^{\rm{T}} } \\ {{{g}}_3} = {\left[ {\begin{array}{*{20}{c}} { - 6.379\;1}&{ - 1.468\;2}&0 \end{array}} \right]^{\rm{T}} } \\ \end{gathered} $ |
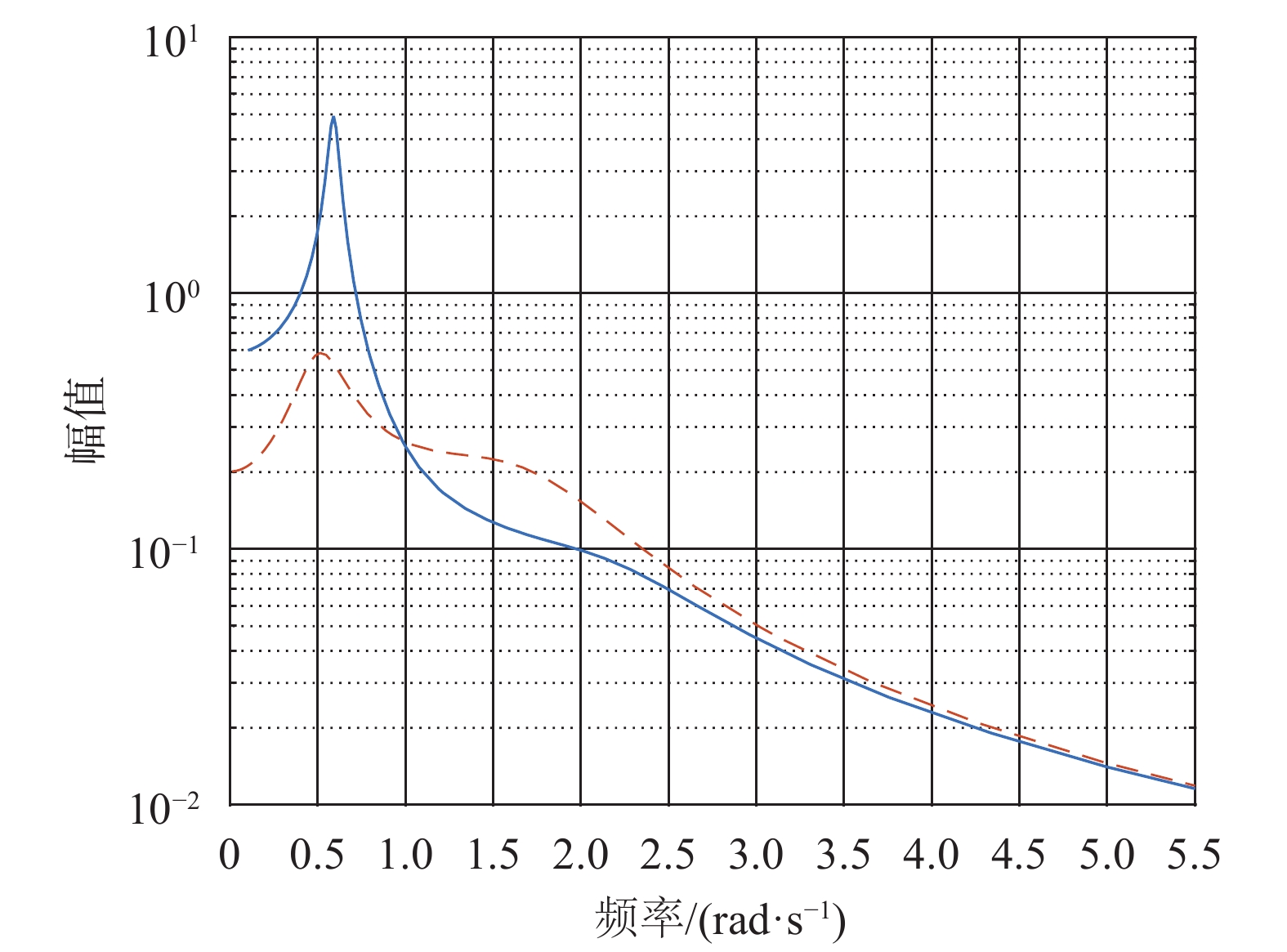
同时计算此时闭环极点为:–0.143 9±0.504 7i,–0.619 5±1.682 4i,–1.019 9±0.952 2i,–3.440 4。极点均分布于虚轴左半平面,闭环系统稳定。同样给出修改后系统H33处的频率响应曲线、零极点分布图及奈奎斯特图如图6~图8所示。由图7及图2对比可知系统零点被准确地分配至预设值。结合图6、图4、图8可看出重分配零点后,系统稳定性增强。证实了方法的有效性。
|
| 图 6 原系统H33(实线)及修改系统H33(虚线)频率响应 Fig. 6 The original system H33 (solid line) and modification system H33 (dotted line) frequency response |

|
| 图 7 修改系统H33零极点分布 Fig. 7 The modification system H33 pole-zero map |
|
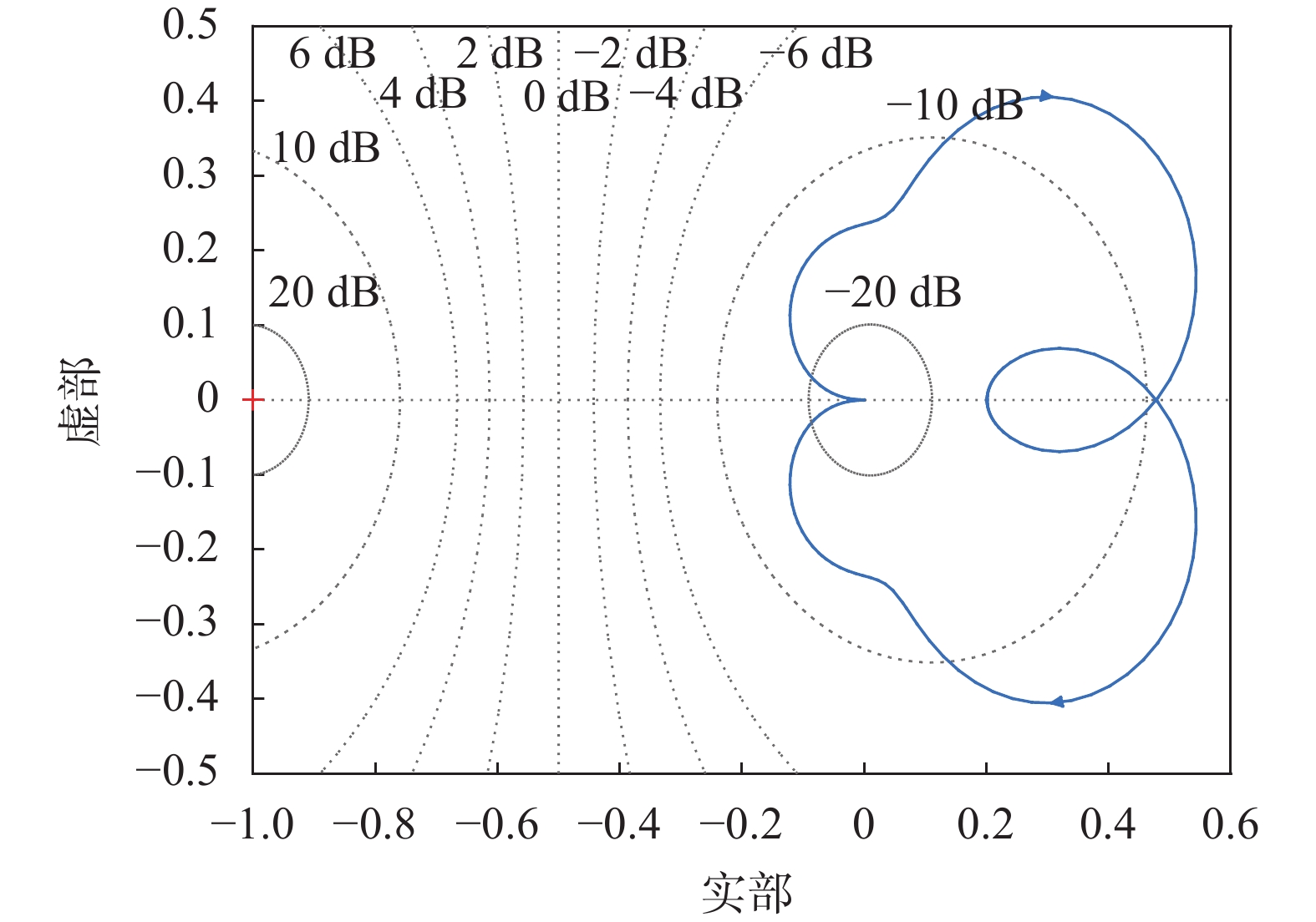
| 图 8 修改系统H33奈奎斯特曲线 Fig. 8 The modification system H33 Nyquist curve |
3.4 零极点分配数值实例
考虑例3.1中三自由度阻尼-质量-弹簧系统,设
联合式(14)及式(22)可得此时
| $\begin{gathered} {{{g}}_1} = {\left[ {\begin{array}{*{20}{c}} {1.962\;3}&{ - 3.044\;8}&0 \end{array}} \right]^{\rm{T}} } \\ {{{g}}_2} = {\left[ {\begin{array}{*{20}{c}} { - 1.321\;5}&{ - 0.491\;2}&0 \end{array}} \right]^{\rm{T} }} \\ {{{g}}_3} = {\left[ {\begin{array}{*{20}{c}} { - 6.379\;1}&{ - 1.468\;2}&0 \end{array}} \right]^{\rm{T}} } \\ \end{gathered} $ |
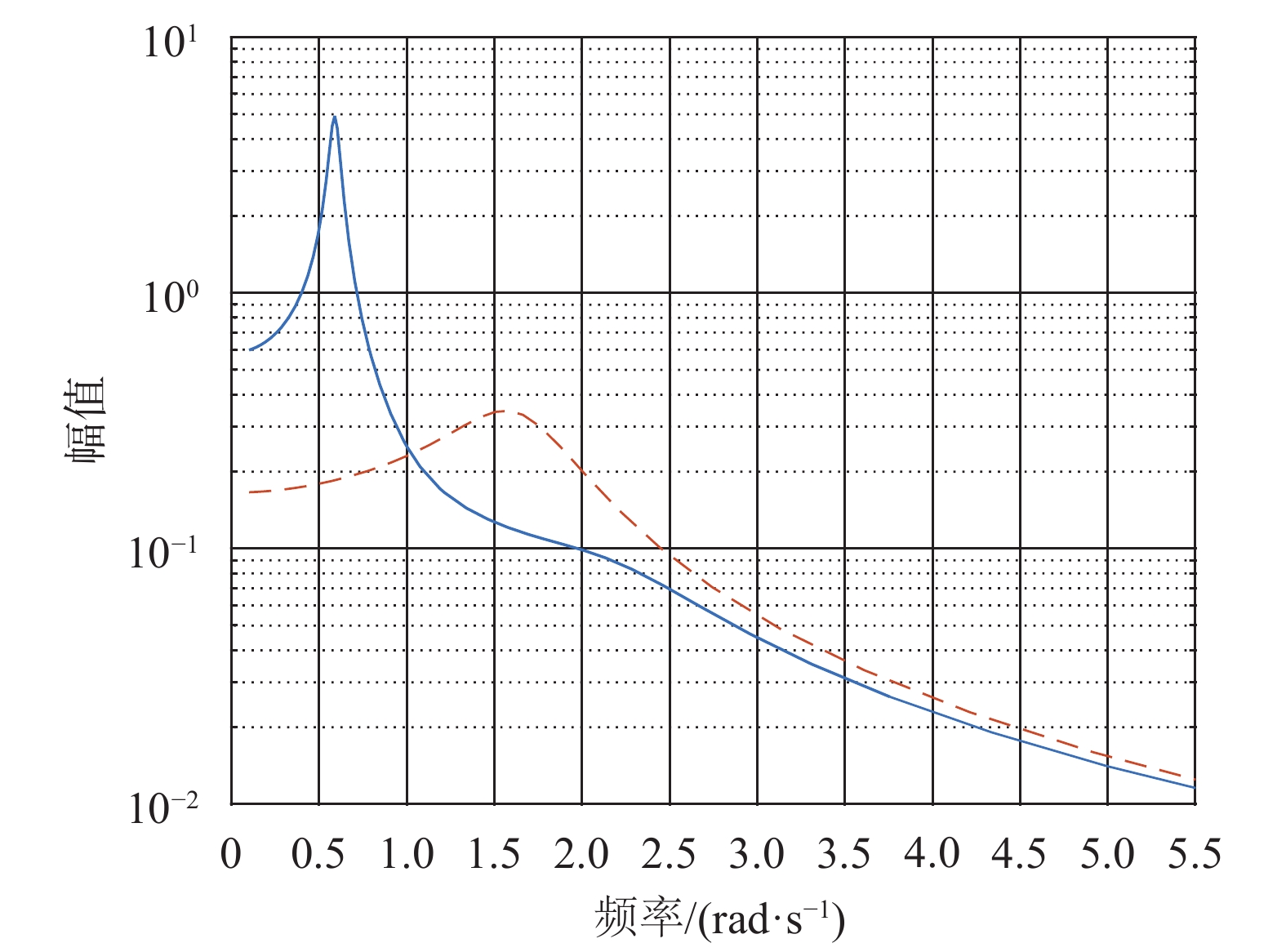
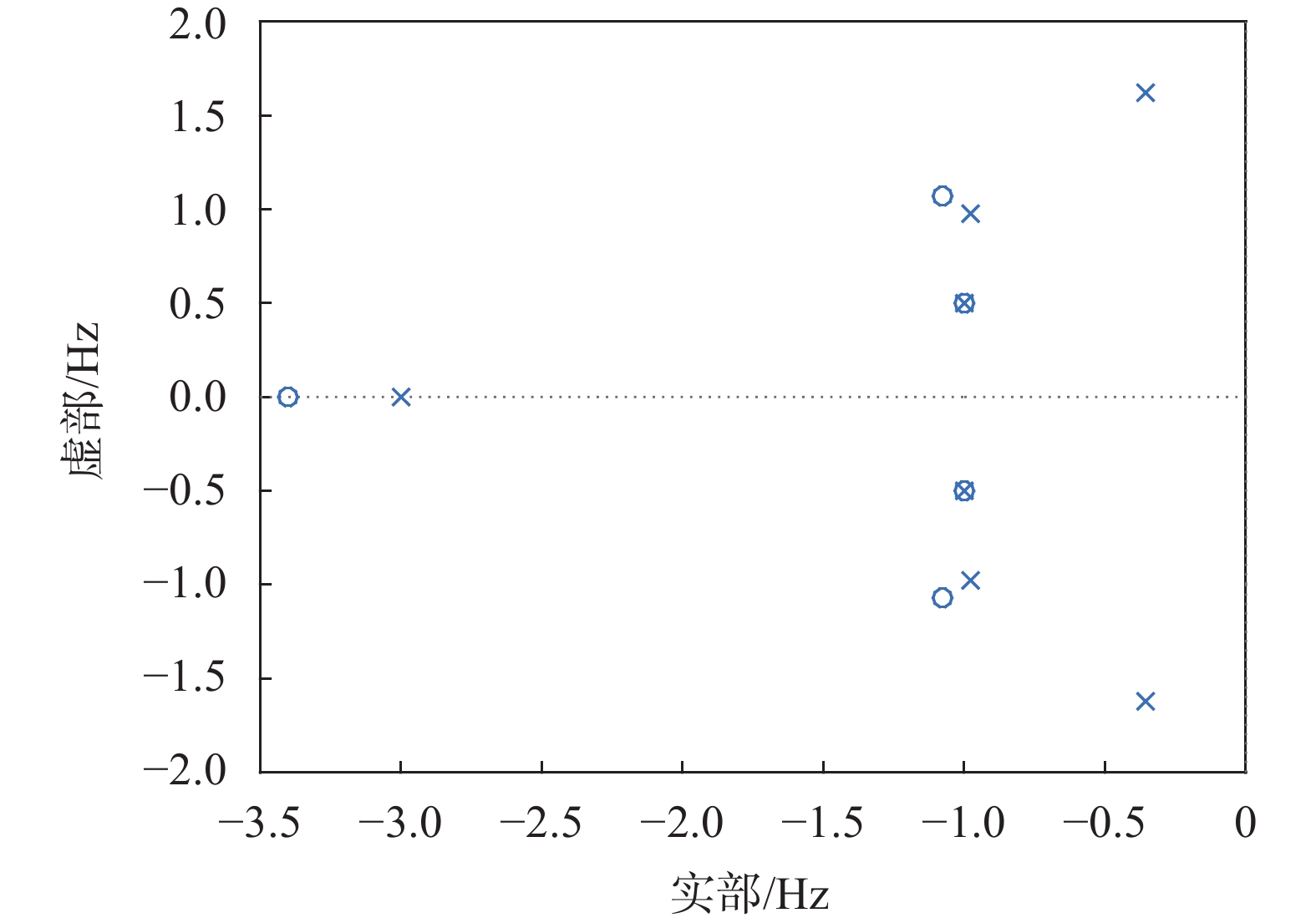
计算此时闭环极点为:–0.356 3±1.621 3i,–0.977 8±0.976 9i,–1±0.5i,–3,均分布于虚轴左半平面,闭环系统稳定。修改后系统H33处的频率响应曲线、零极点分布图及奈奎斯特图如图9~图11所示。由图10及图2对比可知系统极点与零点被准确地分配至预设值。结合图9、图4、图11可看出重分配零点后,系统稳定性增强。证实了方法的有效性。
|
| 图 9 原系统H33(实线)及修改系统H33(虚线)频率响应 Fig. 9 The original system H33 (solid line) and modification system H33 (dotted line) frequency response |
|
| 图 10 修改系统H33零极点分布 Fig. 10 The modification system H33 pole-zero map |

|
| 图 11 修改系统H33奈奎斯特曲线 Fig. 11 The modification system H33 Nyquist curve |
4 结束语
本文通过理论推导得到了基于动柔度法的PID主动振动控制零极点配置算法。本方法用于闭环系统极点及零点的分配,以获得良好的阻尼比及模态频率。修改后的闭环系统固有特性得到控制及改善,从而可以在工作频率段达到避振的控制效果。另外该方法由于引入了积分控制,从而避免了系统成为非奇异系统保证了系统的正定性并拓展了动柔度法的应用范围。同时提出确定可配置闭环极点数目的重要性及计算方法,并讨论了缺少极点分配的情况。最后讨论了选择性分配反馈增益的方法,为后文在实践中获取最佳的反馈控制方案做了初步探索。
| [1] |
BAUOMY H S. Active vibration control of a dynamical system via negative linear velocity feedback[J].
Nonlinear Dynamics, 2014, 77(1-2): 1-11.
DOI:10.1007/s11071-014-1248-x |
| [2] |
JIFFRI S, LI D, XIANG J, et al. Feedback linearisation of nonlinear vibration problems: A new formulation by the method of receptances[J].
Mechanical Systems & Signal Processing, 2018, 98: 1056-68.
|
| [3] |
WEI X J. Active vibration control in linear time-invariant and nonlinear systems[D]. Liverpool: University of Liverpool, 2015.
|
| [4] |
WEI X, MOTTERSHEAD J E. Block-decoupling vibration control using eigenstructure assignment[J].
Mechanical Systems & Signal Processing, 2016, 74: 11-28.
|
| [5] |
RAM Y M, MOTTERSHEAD J E. Receptance method in active vibration control[J].
Aiaa Journal, 2006, 45(3): 562-567.
|
| [6] |
MOTTERSHEAD J E, TEHRANI M G, RAM Y M. Assignment of eigenvalue sensitivities from receptance measurements[J].
Mechanical Systems & Signal Processing, 2009, 23(6): 1931-9.
|
| [7] |
MOTTERSHEAD J E, TEHRANI M G, JAMES S, et al. Active vibration suppression by pole-zero placement using measured receptances[J].
Journal of Sound & Vibration, 2008, 311(3-5): 1391-408.
|
| [8] |
ZHANG J, OUYANG H, YANG J. Partial eigenstructure assignment for undamped vibration systems using acceleration and displacement feedback[J].
Journal of Sound & Vibration, 2014, 333(1): 1-12.
|
| [9] |
OUYANG H. Pole assignment of friction-induced vibration for stabilisation through state-feedback control[J].
Journal of Sound & Vibration, 2010, 329(11): 1985-91.
|
| [10] |
SAMIN R, TEHRANI M G, MOTTERSHEAD J E. Active vibration suppression by the receptance method: partial pole placement, robustness and experiments[C]//Vibration Problems ICOVP 2011, Springer Proceedings in Physics. Dordrecht: Springer, 2011.
|
| [11] |
ISHIHARA J Y, TERRA M H. On the Lyapunov theorem for singular systems[J].
IEEE Transactions on Automatic Control, 2002, 47(11): 1926-30.
DOI:10.1109/TAC.2002.804463 |
| [12] |
RAM Y M. Pole-zero assignment of vibratory systems by state feedback control[J].
Journal of Vibration & Control, 1998, 4(2): 145-65.
|
 2019, Vol. 45
2019, Vol. 45



