文章信息
- 黄慧杰, 孙百祎, 任学平, 刘淮全
- HUANG Huijie, SUN Baiyi, REN Xueping, LIU Huaiquan
- 基于CEEMDAN和1.5维谱的滚动轴承早期故障诊断方法
- Early fault diagnosis of rolling bearing based on CEEMDAN and1.5 dimension spectrum
- 中国测试, 2019, 45(2): 151-156
- CHINA MEASUREMENT & TEST, 2019, 45(2): 151-156
- http://dx.doi.org/10.11857/j.issn.1674-5124.2017100076
-
文章历史
- 收稿日期: 2017-10-23
- 收到修改稿日期: 2018-02-01
2. 山东交通职业学院泰山校区,山东 泰安 271000
2. Taishan Campus of Shandong Transport Vocational College, Taian 271000, China
轴承在机械设备运行中发挥无可替代的作用,发生损伤后,会影响机械设备中其他元件的正常工作,损伤的扩大会导致一系列故障,造成严重经济损失,所以能够对轴承早期故障进行及时地检测和诊断具有重要意义。但轴承出现早期故障时,其故障特征十分微弱,周围环境的干扰会使振动信号复杂化,导致故障特征难以提取[1-3]。
经验模态分解[4](EMD)作为处理复杂信号的工具,得到广泛应用,但是EMD存在模态混叠现象。为了解决这一问题,EEMD[5-6]被提出来,通过向信号中增加高斯白噪声,显著减少模态混叠,但是该方法运算量大,对添加高斯白噪声的标准差以及次数依赖比较大。Torres等[7]提出了一种自适应白噪声的完备总体经验模态分解(CEEMDAN),它能够自适应地选择加噪参数,不仅改善了分解的效果,而且提高了分解的速率。
CEEMDAN作为复杂信号的前处理工具,需要与合适的后处理方法结合才能更好提取故障特征[8]。1.5维谱[9-11]具有基频分量加强特性、耦合谐波分量检测性质以及抑制白噪声等优良特性,这些特性说明1.5维谱在信号的特征提取方面具有一定优势,十分适合作为CEEMDAN的后处理方法。
结合自适应白噪声的完备总体经验模态分解在抗模态混叠方面的优点,以及1.5维谱在特征提取方面的优势,本文提出了将CEEMDAN和1.5维谱相结合的滚动轴承早期故障诊断的方法,并通过仿真信号以及工程实验数据分析验证方法的有效性。
1 基础理论介绍 1.1 CEEMDANEMD将复杂信号分解为多个IMF与残量之和。EEMD是在EMD基础上在每次分解前加入预先设定好的高斯白噪声。CEEMDAN是在每次分解前加入自适应的高斯白噪声来计算唯一残余信号,在该算法中,y(t)为原始信号,用
1)利用EEMD算法分解得到第1个模态分量:
| $ \overline {\rm IMF{_1}} = \frac{1}{N}\sum\limits_i^1 {{\rm IMF}{_i}} $ | (1) |
2)计算第1个残余分量:
| $ {R_1}(t) = y(t) - \overline {\rm IMF{_1}} $ | (2) |
3)进行i次试验每次对R1(t)+
| $ \overline {\rm IMF{_2}} = \frac{1}{N}\sum\limits_i^1 {{E_1}} \left\{ {{R_1}(t) + \varepsilon {E_1}[{n_i}(t)]} \right\} $ | (3) |
4)对于k=2, 3, …, K,计算第k个残余分量:
| $ {R_k}(t) = {y_{k - 1}}(t) - \overline {{\rm IMF}{_k}} $ | (4) |
5)再分别对第k个信号Rk(t)+
| $ \overline {{\rm IMF}{_{{k} + {\rm{1}}}}} = \frac{1}{N}\sum\limits_i^1 {{E_k}} \left\{ {{R_k}(t) + \varepsilon {E_k}[{n_i}(t)]} \right\} $ | (5) |
6)令k=k+1,执行步骤4),直到最后残余量不能再被分解时终止分解。最后的残余量:
| $ \overline {R(t)} = y(t) - \sum\limits_{k = 1}^K {\overline {{\rm IMF}{_{k}}} } $ | (6) |
原始信号:
| $ y(t) = \overline {R(t)} + \sum\limits_{k = 1}^K {\overline {{\rm IMF}{_{k}}} } $ | (7) |
c(
| $\begin{split} {C({\rm{\omega }}_{\rm{0}}}) =& \int_{ - \infty }^{ + \infty } \left[ {\int_{ - \infty }^{ + \infty } {y(t)} {y^2}(t + \tau ){\rm{d}}t} \right]{{\rm e}^{ - {\rm j}{{\rm{\omega }}_{\rm{0}}}\tau }}{\rm{d}}\tau =\\ & {Y^{\rm{*}}}({\omega _{\rm{0}}})[Y({\omega _{\rm{0}}}){\rm *}Y({\omega _{\rm{0}}})] \end{split}$ | (8) |
其中:Y(
1)基频分量加强性质
设振动信号x(t)是均值为零的m次谐波信号,其基频为
| $ B({{\rm{\omega }}_{{i}}}) > B({{\rm{\omega }}_j}) $ | (9) |
其中
2)高斯白噪声的抑制性质
若n(t)为零均值高斯白噪声,则有:
| $ B({{\rm{\omega }}_{\rm{0}}}) = 0 $ | (10) |
表明1.5维谱可以有效抑制高斯白噪声。
3)谐波分量检测性质
设y(t)为一个谐波信号,
这充分说明了经过1.5维谱处理的信号,不存在有3个波形的耦合谐波部分将被消除,存在有3个波形的耦合谐波部分会被提取。
1.3 基于CEEMDAN和1.5维谱的滚动轴承早期故障诊断方法本文将自适应白噪声的完备总体经验模态分解和1.5维谱相结合,提出了一种解决滚动轴承早期故障特征难识别问题的方法,该方法具体实现过程如下:
1)首先利用CEEMDAN将信号分解成一系列IMF分量。
2)根据峭度原则以及相关系数原则选择一个包含主要故障信息的IMF分量。
3)对提取的IMF分量进行Hilbert解调处理得到其包络信号。
4)对提取的IMF分量的包络信号进行1.5维谱分析,得到其1.5维包络谱。
5)通过分析1.5维包络谱来判断轴承的故障类型。
2 仿真信号分析根据滚动轴承外圈故障机理和其振动数学模型[12-13],构造强噪背景下滚动轴承外圈故障振动信号:
| $ \left\{ \begin{array}{l} y(t) = {y_{\rm c}}{{\rm e}^{ - \xi 2\pi {f_{\rm n}}t}}\sin 2\pi {f_{\rm n}}\sqrt {1 - {\varphi ^2}t} \\ x(t) = y(t) + n(t) \end{array} \right. $ | (11) |
其中,轴承固有频率fn=3 000 Hz,位移常数yc=5,阻尼系数
图1(a)为仿真冲击信号。图1(b)为染噪后的仿真信号,从图中可以看出,染噪后的信号十分混乱,冲击特征已经完全被覆盖,毫无规律可寻。
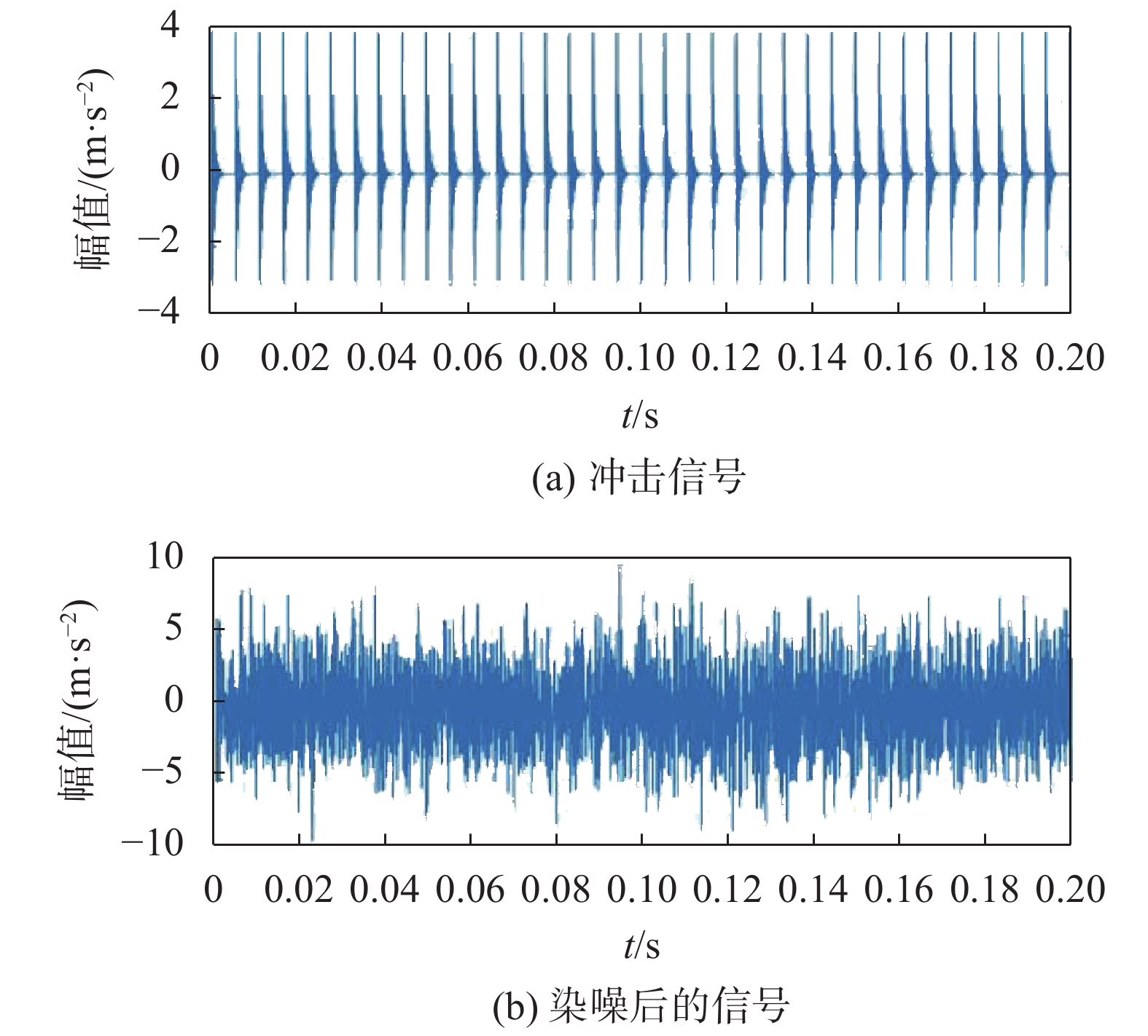
|
| 图 1 仿真信号 |
首先,用CEEMDAN对信号进行自适应分解,得到11个IMF分量以及1个残余分量,如图2所示。然后根据峭度准则以及相关系数准则提取一个包含主要故障信息的IMF分量作为后续分析对象,本次提取的分量为IMF2。图3为IMF2的时域图,从图中可以看到有比较明显的周期性冲击。

|
| 图 2 CEEMDAN分解结果 |
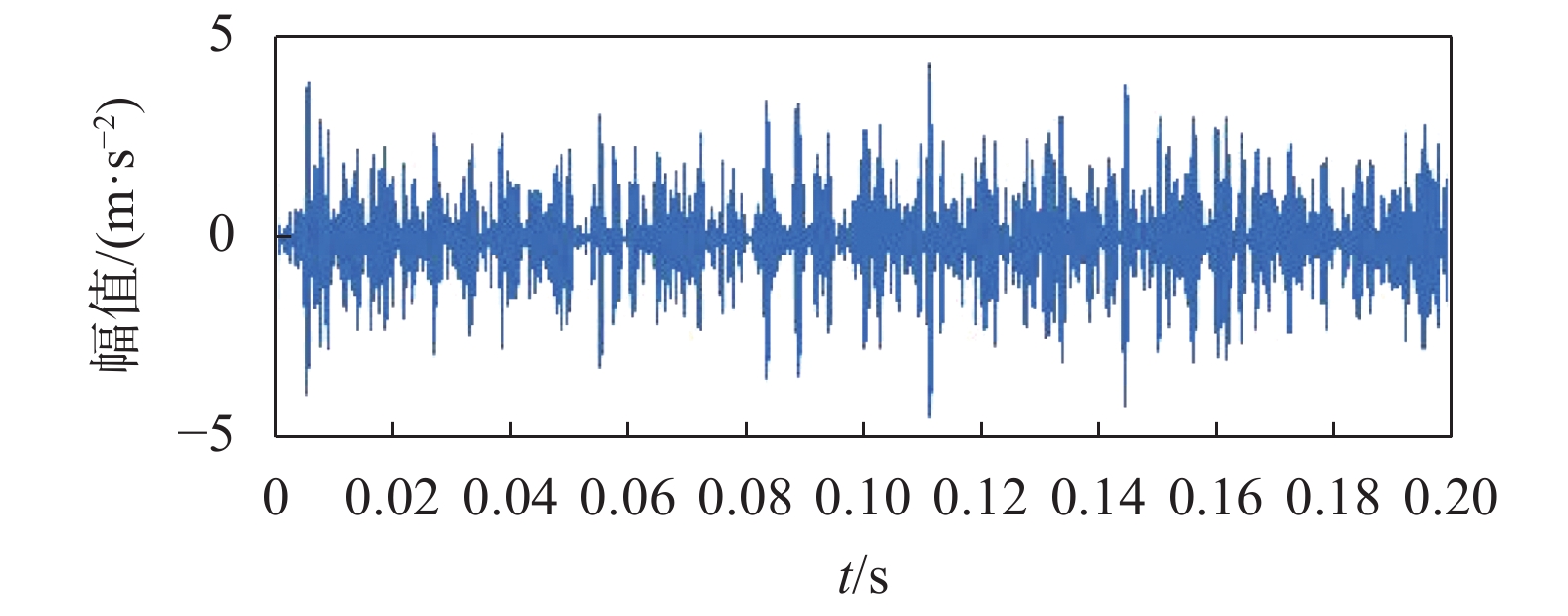
|
| 图 3 提取的分量IMF2 |
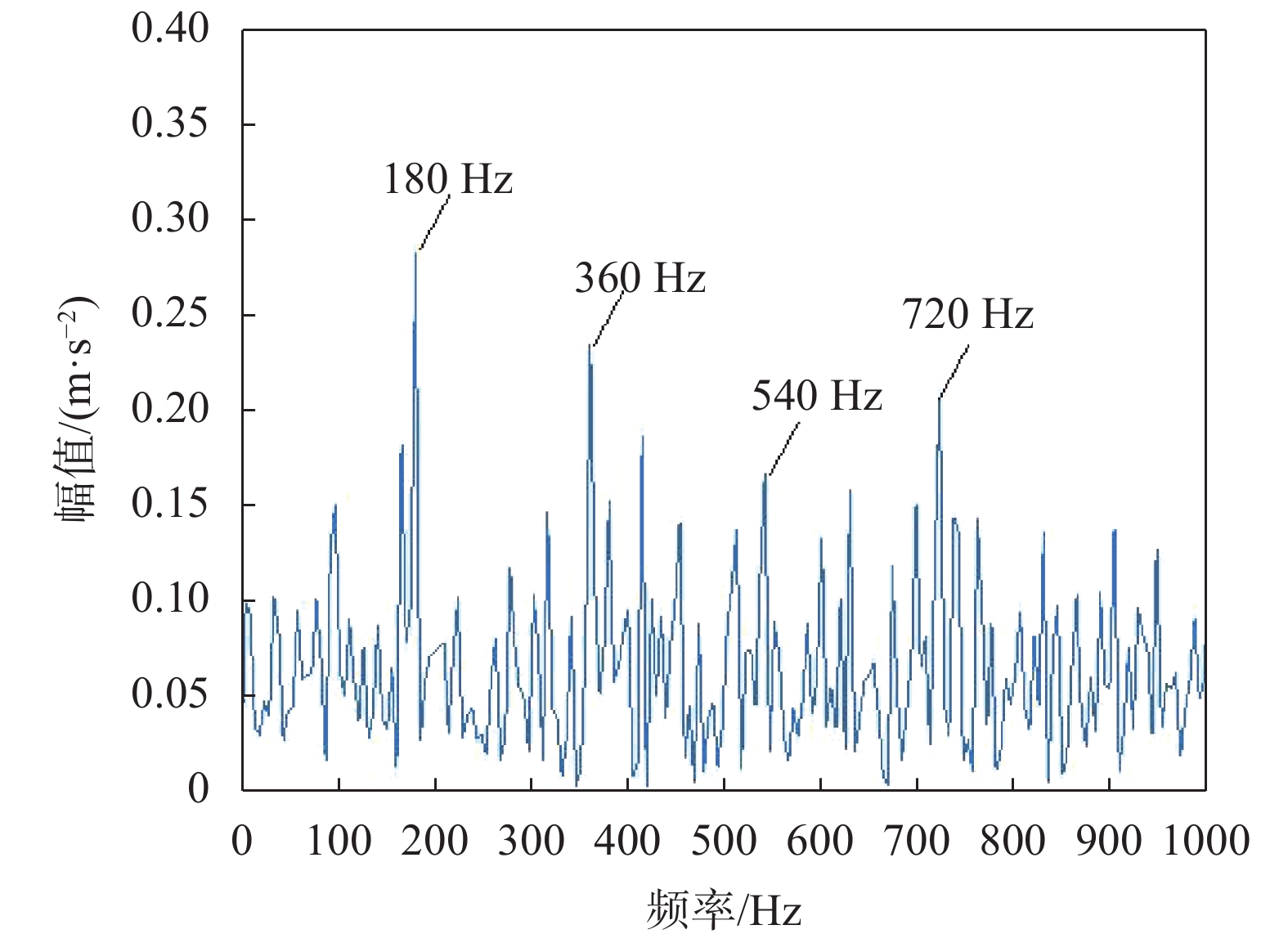
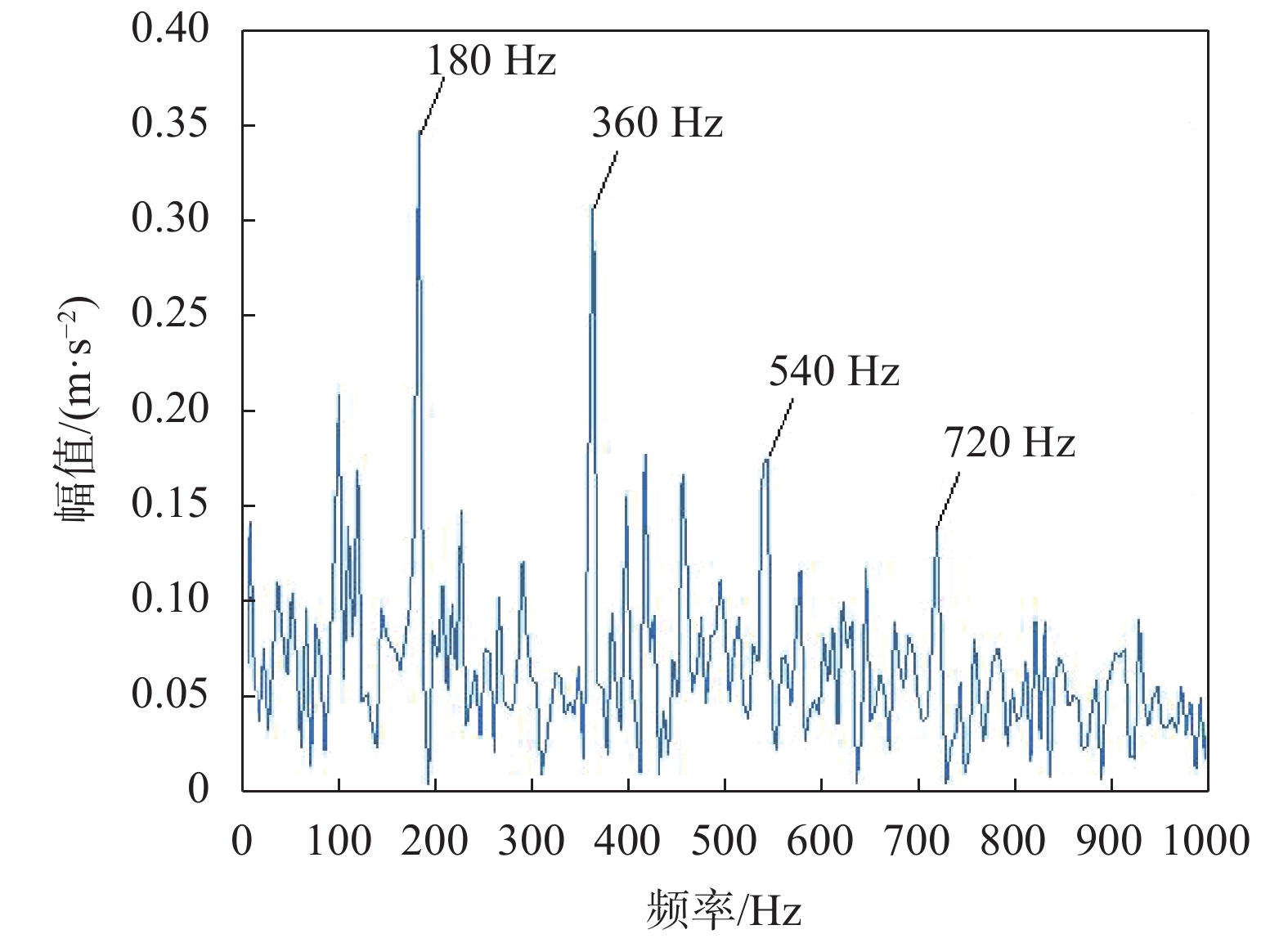
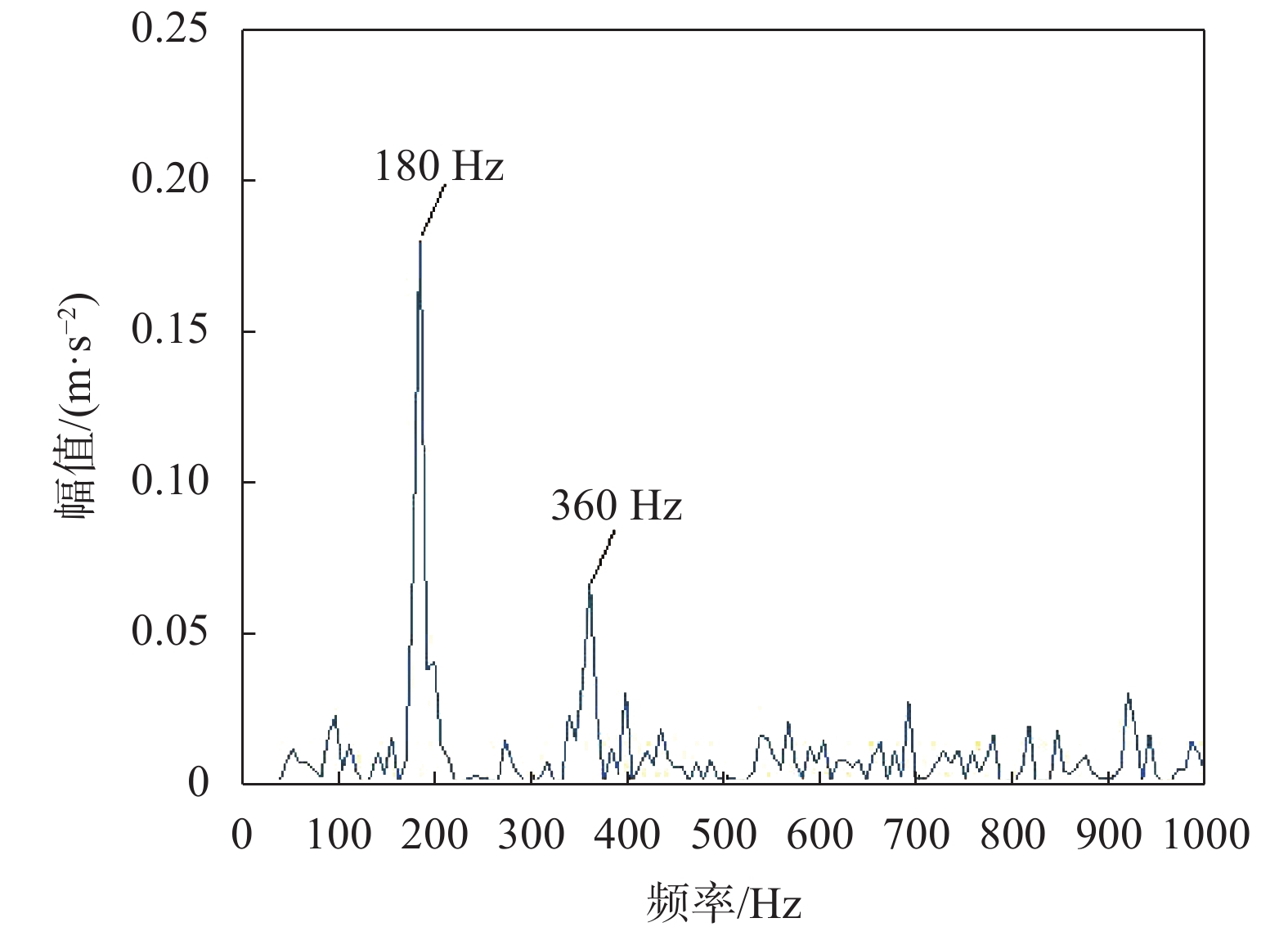
最后,对提取的分量IMF2的包络信号进行1.5维谱分析,得到其1.5维包络谱如图4所示。谱图中清晰看到与故障特征频率fo对应的180 Hz及其倍频成分,并且无太多干扰成分, 故用此方法成功提取出了故障特征信息。图5为原始信号的包络谱,图6为经过CEEMDAN分解后IMF2的包络谱,图7为原始信号的1.5维包络谱,图5、图6、图7中所表现出的特征提取效果都没有图4清晰。经过对比,凸显了将这两种方法结合在早期故障诊断应用上的优势。
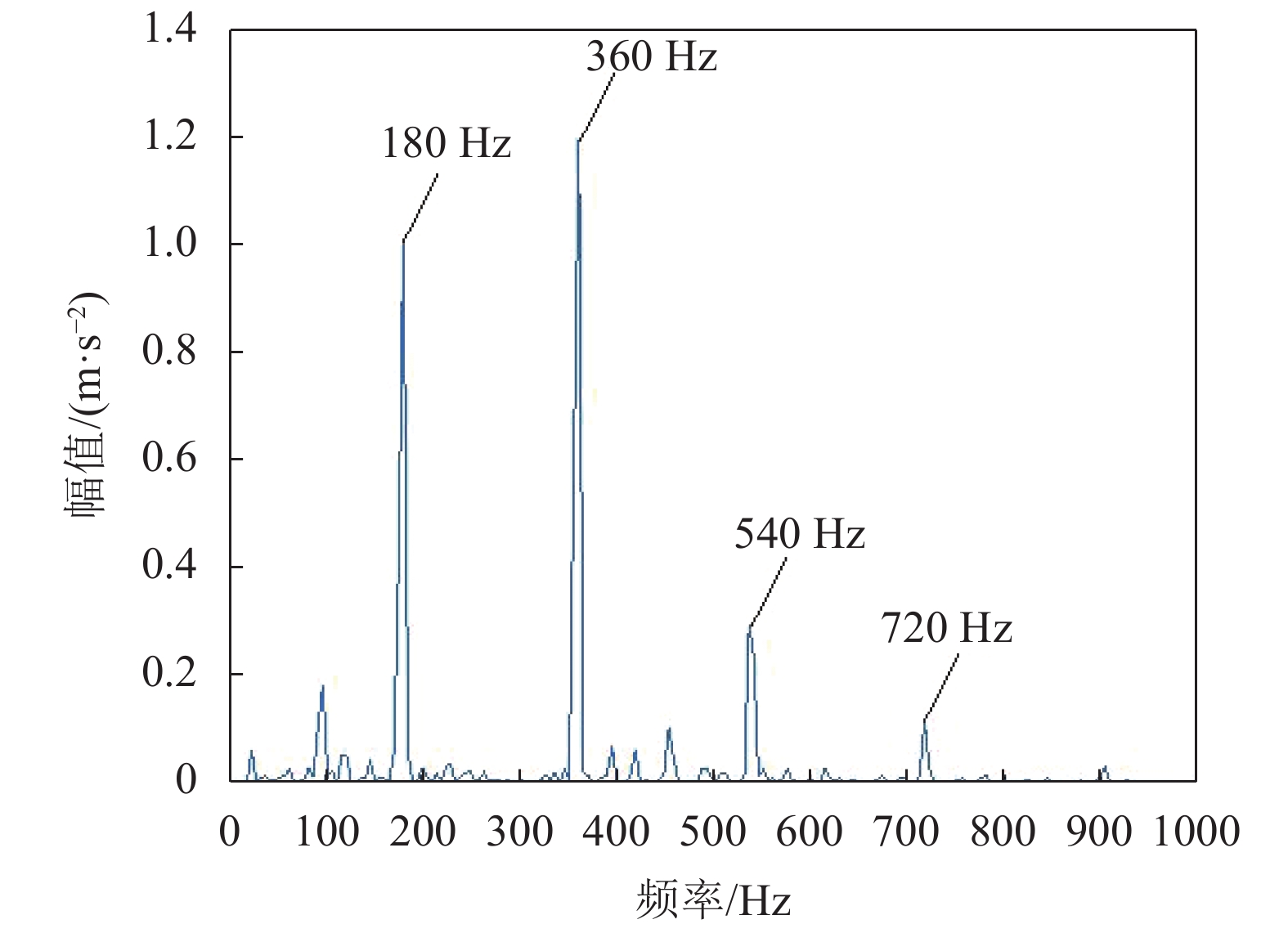
|
| 图 4 IMF2的1.5维包络谱 |
|
| 图 5 原始信号的包络谱 |
|
| 图 6 IMF2的包络谱 |
|
| 图 7 原始信号的1.5维包络谱 |
3 实验分析
本实验采用美国SpectraQuest公司设计的动力与传动故障诊断综合试验台,如图8所示。试验时,故障轴承安设于靠近电机一侧轴承座之上,再安装3个加速度传感器于此轴承座上,分别采集垂直、水平以及轴向方向的振动加速度信号,对应图8中测点1、测点2和测点3,最后通过DT9837型号数据采集仪存储数据于计算机上。

|
| 图 8 故障诊断综合试验台 |
实验采用ER-16K型号的深沟球轴承作为实验对象,为了模拟滚动轴承外圈故障,实验前保持轴承内圈、滚动体完好,对外圈人为加工轻微凹痕(损伤直径0.54 mm,损伤深度0.26 mm)作为轴承外圈早期点蚀故障。实验所用滚动轴承型号具体结构参数如表1所示。
实验开始,设置采样频率为24 000 Hz,电机转速为900 r/min(转频fr=15 Hz),采集数据10 s,并取12 000个数据点作为后续分析。根据下式计算ER-16K滚动轴承外圈故障特征频率为53.655 Hz。
| $ {f_{\rm oc}} = \frac{1}{2}N\left[ {1 - \frac{d}{D}\cos \alpha } \right]{f_{\rm r}} $ | (8) |
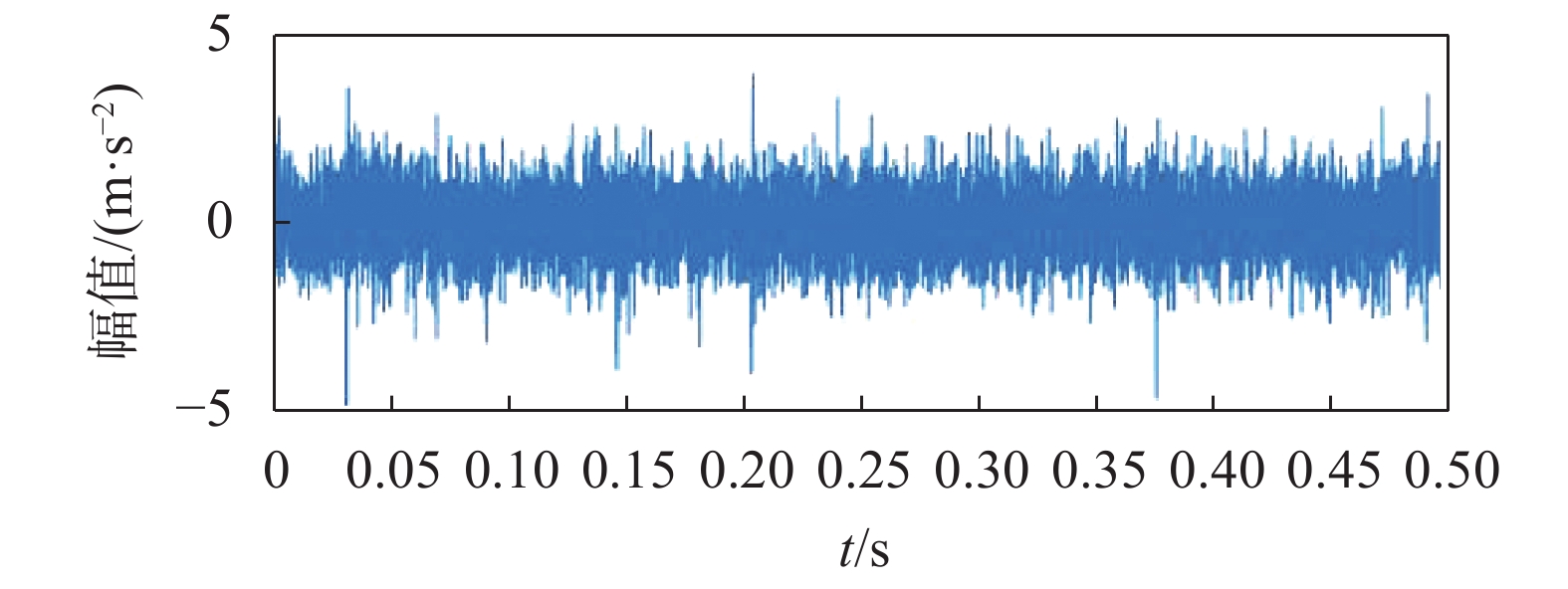
图9为本次实验采集信号的时域波形图,图中并没有发现明显的周期性冲击,早期故障微弱,已被强噪声淹没。
|
| 图 9 实验信号的时域波形 |
首先,用CEEMDAN对信号进行自适应分解,得到13个IMF分量以及1个残余分量。然后根据峭度准则以及相关系数准则提取一个包含主要故障信息的IMF分量,本次提取IMF1作为后续分析对象,如图10所示。
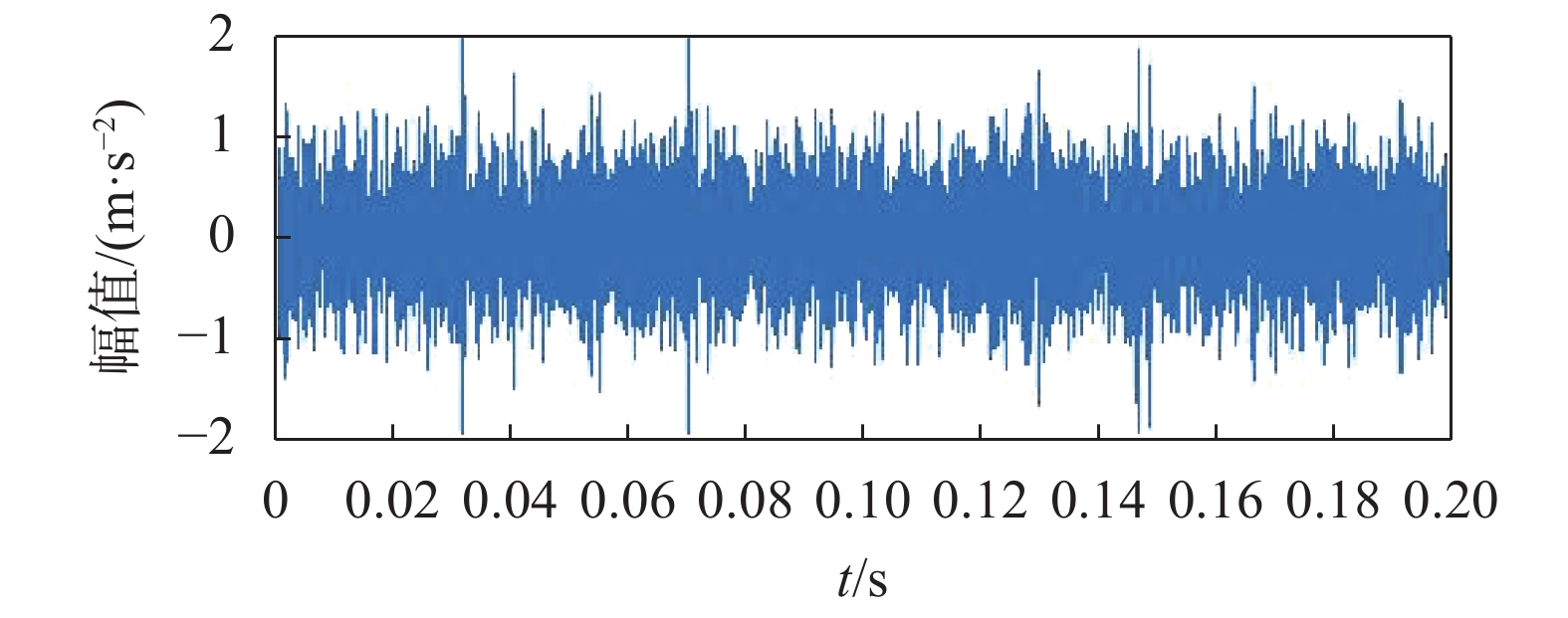
|
| 图 10 提取的分量IMF1 |
最后用1.5维谱算法处理提取分量IMF1的包络信号,得到1.5维包络谱如图11所示。谱图中清晰显示出与故障特征频率相对应的52 Hz及其倍频成分,而且特别清晰,52 Hz与计算所得的滚动轴承外圈故障特征频率53.655 Hz接近,可被认为是外圈故障,至此,本文方法成功提取出了故障特征。作为对比,图12为IMF1分量的包络谱;图13为原始信号的1.5维包络谱;图14为原始信号的包络谱。对比图11与其他谱图,图11故障特征清晰许多,表明该方法在提取早期故障特征具有一定优势。
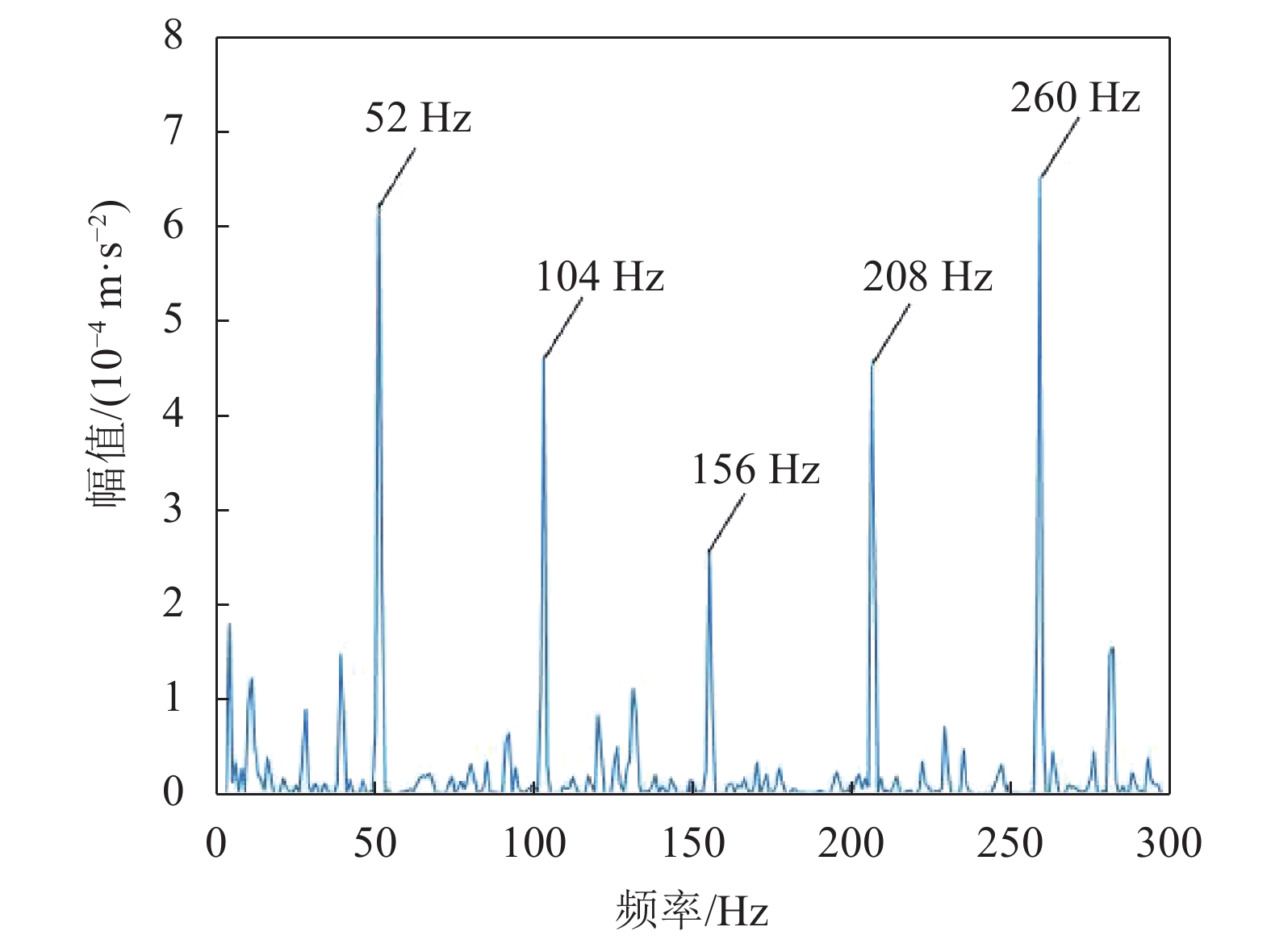
|
| 图 11 IMF1分量的1.5维包络谱 |
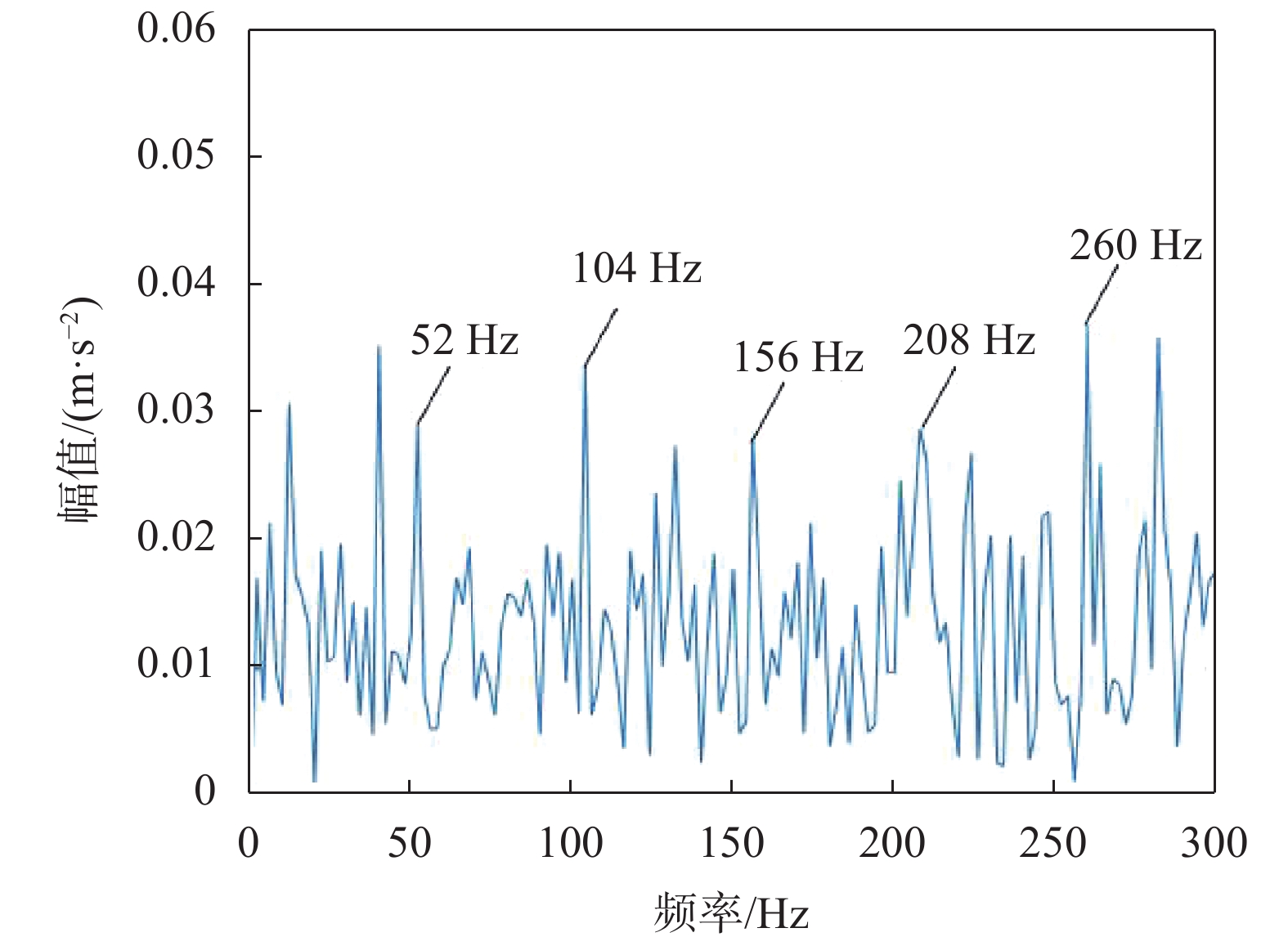
|
| 图 12 IMF1的包络谱 |
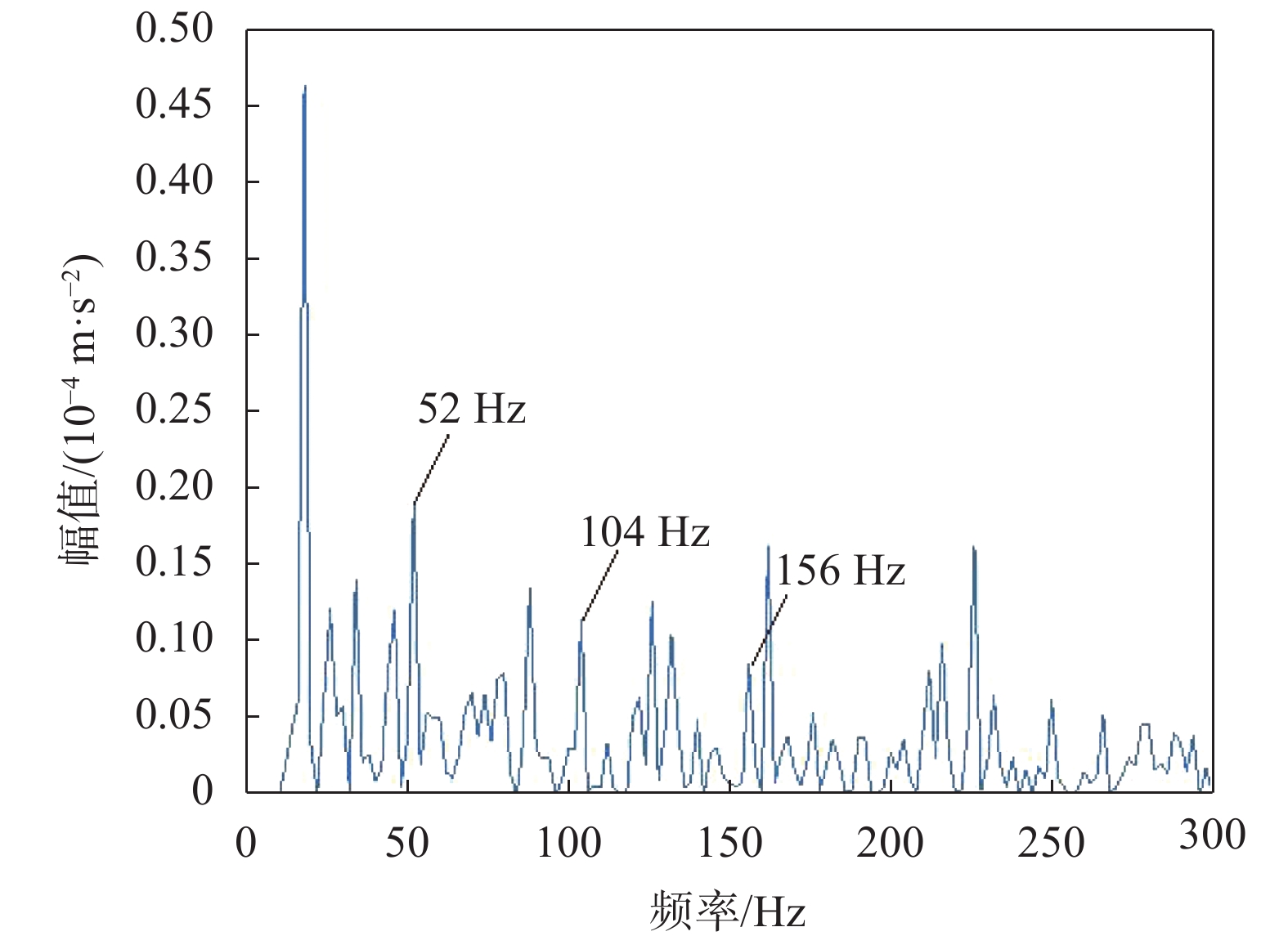
|
| 图 13 原始信号的1.5维谱 |
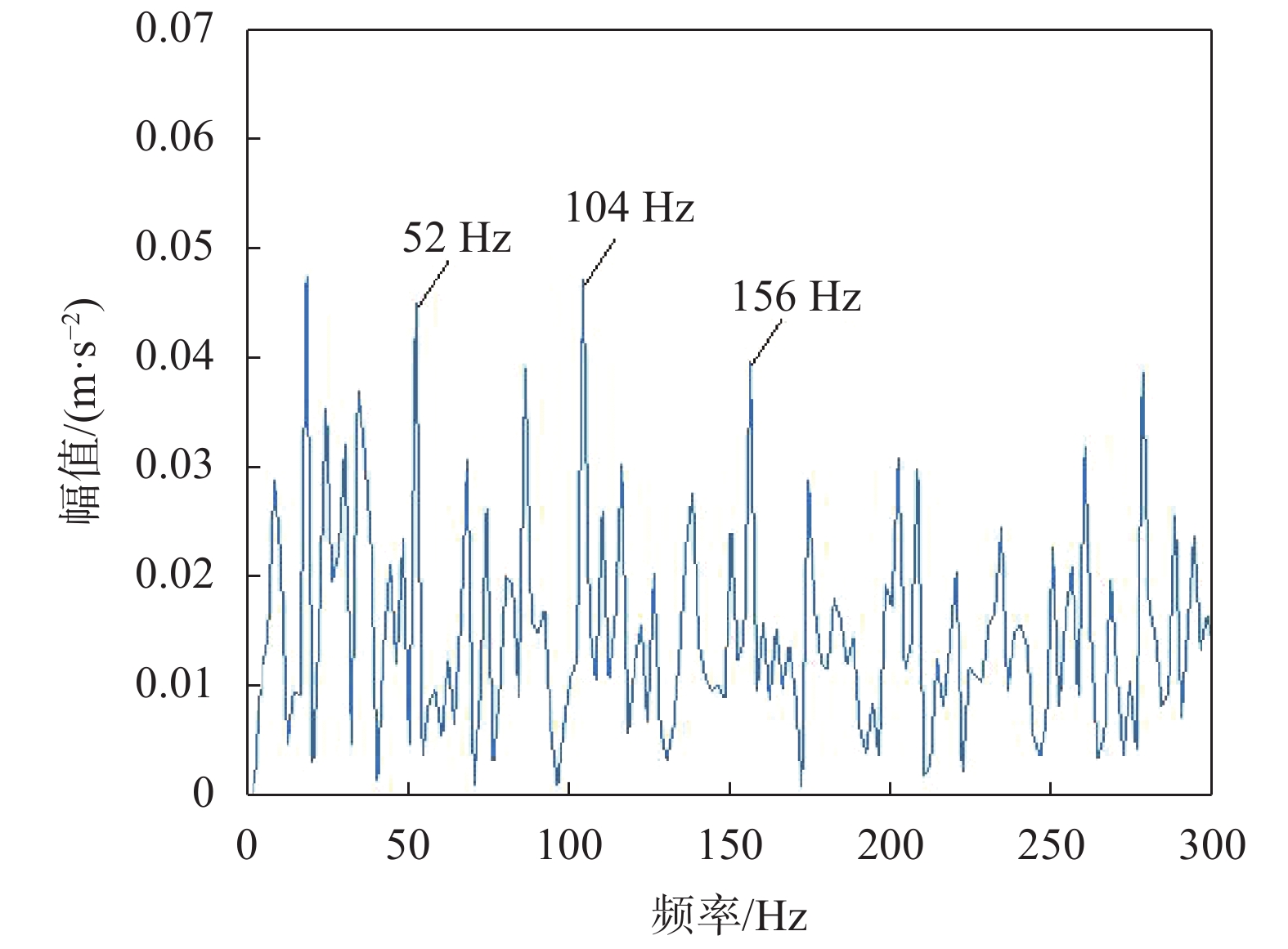
|
| 图 14 实测原始信号包络谱 |
4 结束语
本文研究了基于自适应白噪声的完备总体经验模态分解(CEEMDAN)和1.5维谱的滚动轴承早期故障诊断方法。CEEMDAN可以自适应分解复杂信号,与相关系数准则和峭度准则相结合,提取敏感分量,以降低其他频率的干扰;1.5维谱不仅可以有效抑制白噪声,提高信噪比,还能增强信号的故障冲击成分;本文将CEEMDAN与1.5维谱相结合,通过分析仿真信号以及工程实验数据验证了该方法在诊断滚动轴承早期故障方面具有一定优势。
| [1] |
李志星, 石博强. 自适应奇异值分解的随机共振提取微弱故障特征[J].
农业工程学报, 2017, 33(11): 60-67.
DOI:10.11975/j.issn.1002-6819.2017.11.008 |
| [2] |
任学平, 王朝阁, 张玉皓, 等. 基于双树复小波包自适应Teager能量谱的滚动轴承早期故障诊断[J].
振动与冲击, 2017, 36(10): 84-92.
|
| [3] |
王建国, 陈帅, 张超. 噪声参数最优ELMD与LS-SVM在轴承故障诊断中的应用与研究[J].
振动与冲击, 2017, 36(5): 72-78.
|
| [4] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].
Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995.
|
| [5] |
LEI Y, HE Z, ZI Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery[J].
Mechanical Systems & Signal Processing, 2009, 23(4): 1327-1338.
|
| [6] |
LEI Y, ZUO M J. Fault diagnosis of rotating machinery using an improved HHT based on EEMD and sensitive IMFs[J].
Measurement Science & Technology, 2009, 20(12): 125701.
|
| [7] |
TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2011: 4144-4147.
|
| [8] |
张建伟, 侯鸽, 暴振磊, 等. 基于CEEMDAN与SVD的泄流结构振动信号降噪方法[J].
振动与冲击, 2017, 36(22): 138-143.
|
| [9] |
唐贵基, 王晓龙. 最大相关峭度解卷积结合1.5维谱的滚动轴承早期故障特征提取方法[J].
振动与冲击, 2015, 34(12): 79-84.
|
| [10] |
CHEN L, ZI Y Y, HE Z J, et al. Research and application of ensemble empirical mode decomposition principle and 1.5 dimension spectrum method[J].
Journal of Xian Jiaotong University, 2009, 43(5): 94-98.
|
| [11] |
钟先友, 曾良才, 赵春华. 局域均值分解和1.5维谱在机械故障诊断中的应用[J].
中国机械工程, 2013, 24(4): 452-457.
DOI:10.3969/j.issn.1004-132X.2013.04.005 |
| [12] |
ANTONI J, BONNARDOT F, RAAD A, et al. Cyclostationary modelling of rotating machine vibration signals[J].
Mechanical Systems & Signal Processing, 2004, 18(6): 1285-1314.
|
| [13] |
唐贵基, 王晓龙. 自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J].
中国电机工程学报, 2015, 35(6): 1436-1444.
|
 2019, Vol. 45
2019, Vol. 45