文章信息
- 郭宏恩
- GUO Hongen
- 核电汽轮机凝汽器运行参数动态特性仿真研究
- Simulation study on dynamic characteristics of condenser operating parameters of nuclear power steam turbine
- 中国测试, 2019, 45(8): 55-60
- CHINA MEASUREMENT & TEST, 2019, 45(8): 55-60
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018010080
-
文章历史
- 收稿日期: 2018-01-22
- 收到修改稿日期: 2018-03-11
核电技术是20世纪最伟大的发明之一,如何对其进行高效利用成为目前研究领域亟待解决的问题。我国核电起步较晚,截止到2017年,核电装机容量仅占全国电力总装机容量的2.21%,预计在未来的5年里,核电装机容量将增至4%。核电站规模变大的同时,核电汽轮机、蒸汽发生器、发电机等设备不断改进,核电机组运行参数不断优化,使用寿命得到提升,但一些辅机设备发展相对滞后。表面式凝汽器是汽轮机的冷端设备,其内部结构复杂,其内部流动属于耦合相变的复杂换热过程。目前,凝汽器热力设计大多采用经验公式,其动态运行参数的准确性难以保证,对核电热力系统二回路的安全和经济性有较大影响。Patankar等[1]将容积多孔度模型引入凝汽器传热计算中,实现了多节点模型对管壳式换热器简化计算,将管束结构、隔板等作为阻力项加入凝结对流换热模型。Carlucci等[2]对凝汽器内流和传热仿真模型进行了研究,并对现有模型进行改进,找出改善凝汽器真空和尽量减少管束振动的方法。汪国山等[3]基于多孔介质物理概念,编写了用于计算凝汽器内部流动和换热过程的3D数值计算程序,通过大量实验验证了程序的计算精度。侯平利等[4-5]对核电站双背压机组冷端优化进行了大量研究,通过建立考虑高低压汽室压力差异的双背压机组计算模型,分析了压力对机组微增出力的影响。总的来说,凝汽器仿真模型已经较为成熟,但是能够全面考虑不凝气体、相间滑移、凝结水溢流、管束阻力等因素的核电站表面式凝汽器动态参数模型还不多见。本文针对核电站凝汽器进行建模仿真,分析了循环冷却水温度、流量、汽轮机排汽量阶跃变化对凝汽器运行参数动态特性的影响,为核电凝汽器变工况运行提供一定参考。
1 动态参数模型 1.1 研究对象凝汽器是汽轮机的冷凝设备,将汽轮机排汽冷凝成饱和水,其必须在真空条件下工作,利用抽气器将壳侧的不凝结气体抽出,维持一定的真空[6-7]。本文的AP1000核电汽轮机组共有3台凝汽器,布置于低压缸下部,换热管束为钛合金材质,循环冷却水为海水。汽轮机排汽被管侧的海水冷却成凝结水,随后汇集到凝汽器底部的热井,再被凝结水泵升压后送至7号低压加热器。凝汽器为三壳体单流程表面式换热器,海水从凝汽器右侧流入左侧流出。主要设计参数见表1。
| 参数名称 | 参数值 |
| 汽轮机容量/MW | 1 253 |
| 凝汽器设计压力/kPa | 3.89 |
| 冷却水温度/℃ | 20 |
| 壳体冷却面积/m2 | 98 330 |
| 冷却水设计流速/(m·s−1) | 2.4 |
| 冷却管外径/mm | ϕ25.4 |
| 冷却管有效长度/m | 18 |
| 管板材质 | SA516Gr60+SB265Gr1 |
| 冷却管材质 | SA285GrC |
1.2 凝汽器热力模型
凝汽器中蒸汽的凝结压力是负荷的函数,主要与凝汽器蒸汽流量、循环冷却水流量、循环冷却水温度有关[8]。当循环冷却水参数不变时,随着机组负荷的增加,凝结压力上升[9]。凝汽器内部热力学特性可通过热力特性方程进行描述:
| $Q = {W_{\rm{t}}}({H_{\rm{s}}} - {H_{\rm{w}}}) = k\Delta {T_{\rm{m}}}A = {W_{\rm{c}}}{C_{\rm{p}}}({T_{{\rm{cout}}}} - {T_{{\rm{cin}}}})$ | (1) |
式中:Q——机组负荷,kW;
Wt——蒸汽流量,kg/s;
Hs——凝汽器入口蒸汽焓,kJ/kg;
Hw——凝汽器内饱和水焓,kJ/kg;
k——凝汽器总传热系数,kW/(m2·K);
ΔTm——对数传热温差,K;
A——凝汽器总换热面积,m2;
Wc——循环冷却水流量,kg/s;
Cp——循环冷却水比热容,kJ/(kg·K);
Tcin、Tcout——循环冷却水进出口温度,K。
对数传热温差[9]:
| $\Delta {T_{\rm{m}}} = \frac{{{T_{{\rm{cout}}}} - {T_{{\rm{cin}}}}}}{{\ln \displaystyle\frac{{{T_{\rm{1}}} - {T_{{\rm{cin}}}}}}{{{T_{\rm{1}}} - {T_{{\rm{cout}}}}}}}}$ | (2) |
其中T1为壳侧饱和蒸汽温度,K。
凝汽器壳侧阻力主要与蒸汽流速有关,但是凝汽器内有上万根管道,因此蒸汽流动阻力变化非常复杂。蒸汽壳侧阻力计算式为
| ${p_{\rm{k}}} = 0.016{\left( {\frac{{{W_{\rm{t}}}\sqrt {{\upsilon _{\rm{s}}}} }}{{L{d_0}\sqrt N }}} \right)^{2.5}}$ | (3) |
式中:
L——冷却管有效长度,m;
d0——冷却管外径,mm;
N——管道个数。
目前,凝汽器热力计算常用的总传热系数公式包括:美国HEI公式、英国BEAMA公式、前苏联别尔曼公式、分部计算关系式等。本文采用分部计算关系式对总传热系数进行计算[6]。凝汽器总换热系数的倒数由水-管对流换热系数、金属管导热系数、管内外污垢层导热系数和壳侧蒸汽-管凝结换热系数5部分组成,总传热系数:
| $\begin{split} k =& \left[\frac{1}{{{\alpha _{\rm{w}}}}} \times \frac{{{d_0}}}{{{d_{\rm{i}}}}} + \frac{1}{{{\alpha _0}\varepsilon _0^{ - 0.04}}} + \frac{{{d_0}}}{{2\lambda }}\ln \frac{{{d_0}}}{{{d_{\rm{i}}}}} \right.+ \\ &\left. {d_0}\frac{1}{{2\pi l{\lambda _2}}}\ln \frac{{{d_0} + 2{\delta _2}}}{{{d_0}}} + \frac{1}{{2\pi l{\lambda _3}}}\ln \frac{{{d_{\rm{i}}}}}{{{d_{\rm{i}}} - 2{\delta _3}}}\right]^{ - 1} \end{split} $ | (4) |
式中:αw——循环水与管道的对流换热系数,kW/(m2·K);
α0——蒸汽与管壁的对流换热系数,kW/(m2·K);
l——单程管道长度,m;
λ——管道导热系数,kW/(m·K);
λ2——管壁上水膜的导热系数,kW/(m·K);
λ3——管内污垢导热系数,kW/(m·K);
di——管道内径,m;
δ2——水膜厚度,m;
δ3——管内污垢厚度,m。
1.3 凝汽器动态参数模型目前,凝汽器动态参数模型多为单压力多节点,并未考虑蒸汽流速、密度等因素引起的沿程阻力。本文采用多压力多节点模型,将凝汽器分为多个控制容积,分别列出每个控制容积的动量方程,进而得到动态参数模型。与单节点模型相比,多节点模型可根据不同控制容积内部压力准确查取工质的物性参数。建立模型之前,应当进行以下假设[10-11]:1)蒸汽和循环冷却水均为定向流动;2)凝汽器内部汽液两相流处于热力平衡状态;3)不考虑汽液两相流相间滑移;4)沿着工质流动方向,各控制容积均匀分布;5)将凝汽器内部的不凝气体视为理想气体。本文研究对象为单流程表面式换热器,管侧的循坏冷却水为单相流体,壳侧的工质为相变流体。将凝汽器内部划分为多个控制容积,每个控制容积包括:蒸汽、循坏冷却水、管壁3部分。控制容积划分情况如图1所示。
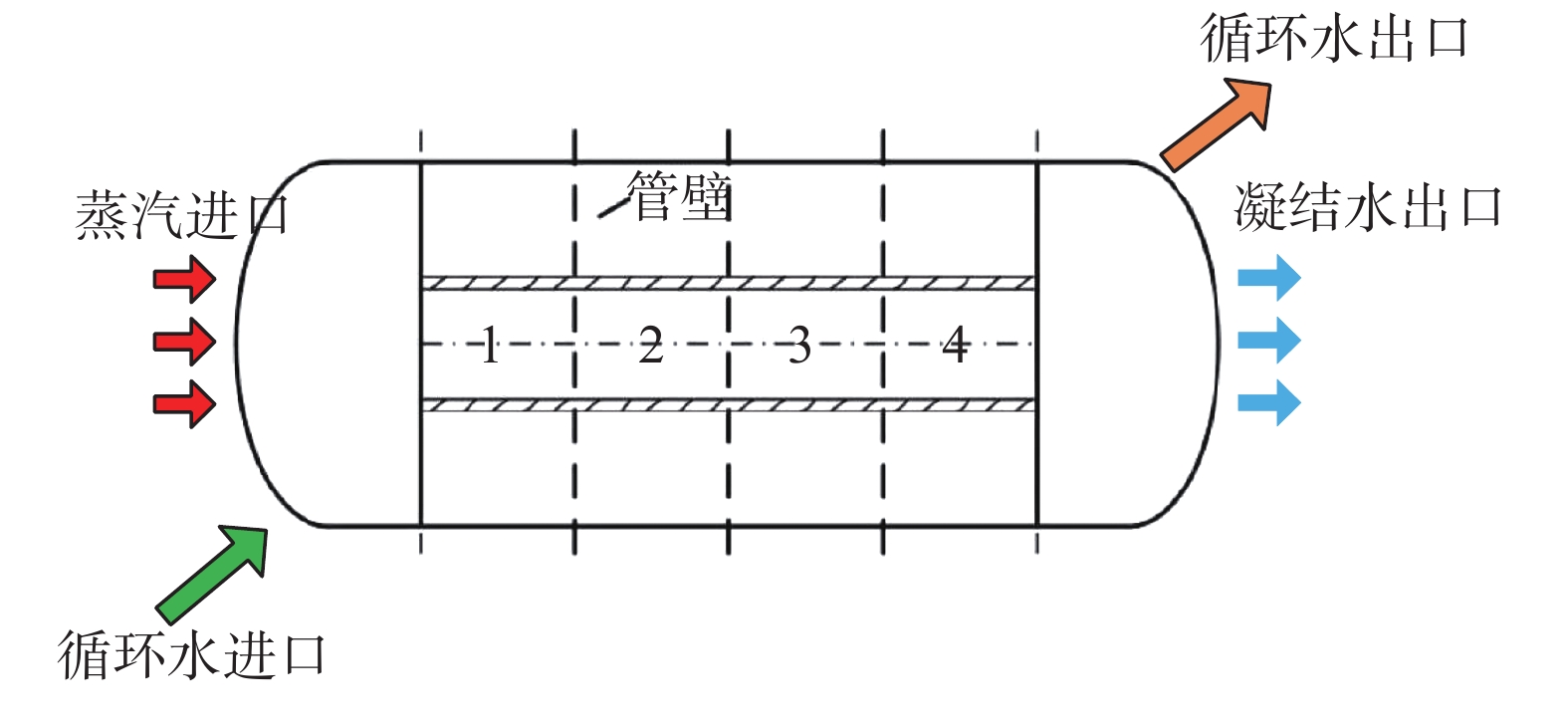
|
| 图 1 控制容积划分示意图 |
图1将整个凝汽器划分为4个相同的控制容积。沿蒸汽流动方向,各控制容积压力下降,对应的水蒸气物性参数发生变化。建立凝汽器二维仿真模型并对其进行求解,得到不同控制容积内压力、流量、温度等参数的变化规律。
各控制容积内壳侧蒸汽质量守恒方程:
| $\frac{{{\rm{d}}{m_{\rm i}}}}{{{\rm{d}}t}} = {m_{{\rm{t,i}}}} + {m_{{\rm{o,i}}}} + {m_{{\rm{f,i}}}} + {m_{{\rm{dv,i}}}} - {m_{{\rm{dc,i}}}} - {m_{{\rm{c,i}}}} - {m_{{\rm{da,i}}}} - {m_{{\rm{air,i}}}}$ | (5) |
式中:mi——汽液两相流质量流量,kg/s;
mt,i——凝汽器入口质量流量,kg/s;
mo,i——辅机排汽质量流量,kg/s;
mf,i——排入凝汽器的水蒸发质量流量,kg/s;
mdv,i——热井中的水蒸发质量流量,kg/s;
mdc,i——热井中水凝结质量流量,kg/s;
mc,i——汽轮机排汽凝结质量流量,kg/s;
mda,i——壳体外侧与空气换热而凝结的蒸汽质量流量,kg/s;
mair,i——不凝结气体质量流量,kg/s。
对于三壳体单流程表面式换热器,入口蒸汽质量流量为未知数,因此其数值需要根据压降进行动态调整。计算前应先假设一个蒸汽质量流量初始值,在根据压降平衡对各控制容积内的蒸汽流量进行动态调整,入口蒸汽质量流量动态关系式为
| $m_{\rm{i}}^{{{t +{\rm d}t}}} = m_{\rm{i}}^{{t}} + \Delta t\left( {\frac{{\Delta P_{\rm{i}}^{{t}} - \Delta P_{{\rm{av}}}^{{t}}}}{{\Delta P_{{\rm{av}}}^{{t}}}}} \right) \times \frac{{m_{\rm{i}}^{{t}}}}{{j - 2}}$ | (6) |
式中:Δ
Δ
Δt——时间差值,s。
不凝气体质量流量动态关系式:
| $\frac{{{\rm{d}}{m_{{\rm{air}},{\rm i}}}}}{{{\rm{d}}t}} = {m_{{\rm{airin}},{\rm i}}} - {m_{{\rm{airout}},{\rm i}}}$ | (7) |
式中:mairin,i——汽轮机排汽带入的不凝气体质量流量,kg/s;
mairout,i——抽气器抽出的不凝气体质量流量,kg/s。
各控制容积汽水混合物平均焓,可由上一时刻平均焓和该时刻各排汽流量焓值共同计算得到[12]。内壳侧蒸汽能量守恒方程:
| $\begin{split} h_{{\rm{iav}}}^{{{t + {\rm d}t}}} =& h_{{\rm{iav}}}^{{t}} + \\&\left[ {\frac{\begin{array}{l} {m_{{\rm{t,i}}}}{h_{{\rm{t,i}}}} + {m_{{\rm{o,i}}}}{h_{{\rm{o,i}}}} + ({m_{{\rm{f,i}}}} + {m_{{\rm{dv,i}}}}){h_{{\rm{c,i}}}} - \\ ({m_{{\rm{dc,i}}}} + {m_{{\rm{c,i}}}} + {m_{{\rm{da,i}}}} + {m_{{\rm{air,i}}}})h_{{\rm{iav}}}^{\rm{t}} \\ \end{array} }{{{m_{{\rm{t,i}}}} + {m_{{\rm{o,i}}}} + {m_{{\rm{f,i}}}} + {m_{{\rm{dv,i}}}} - {m_{{\rm{dc,i}}}} - {m_{{\rm{c,i}}}} - {m_{{\rm{da,i}}}}}}} \right]{\rm{d}}t\end{split}$ | (8) |
式中:
ht,i——各控制容积进口蒸汽焓,kJ/kg;
ho,i——辅机排汽焓,kJ/kg;
hc,i——凝结水焓,kJ/kg。
循环冷却水出口温度:
| $T_{{\rm{cout,i}}}^{{{t + {\rm d}t}}} = T_{{\rm{cout,i}}}^{{t}} + 2 \times \frac{{{Q_{{\rm{c,i}}}} - {W_{{\rm{c,i}}}}(T_{{\rm{cout,i}}}^{{t}} - T_{{\rm{cin,i}}}^{{t}})}}{{{m_{{\rm{c,i}}}}{C_{{\rm{p,i}}}}}}{\rm{d}}t$ | (9) |
其中Qc,i为各节点循环冷却水换热量,W。
采用交错网格技术对凝汽器压力场进行处理,将压力、温度分布在主网格上,将流量分布在网格界面节点上,采用Adams多步仿真算法进行求解。对于二维计算问题,流量计算值要比温度、压力滞后半个步长时间,参数值主要通过节点内部积分求得,压力梯度通过两个相邻容积的压力值进行描述。计算流程见图2。
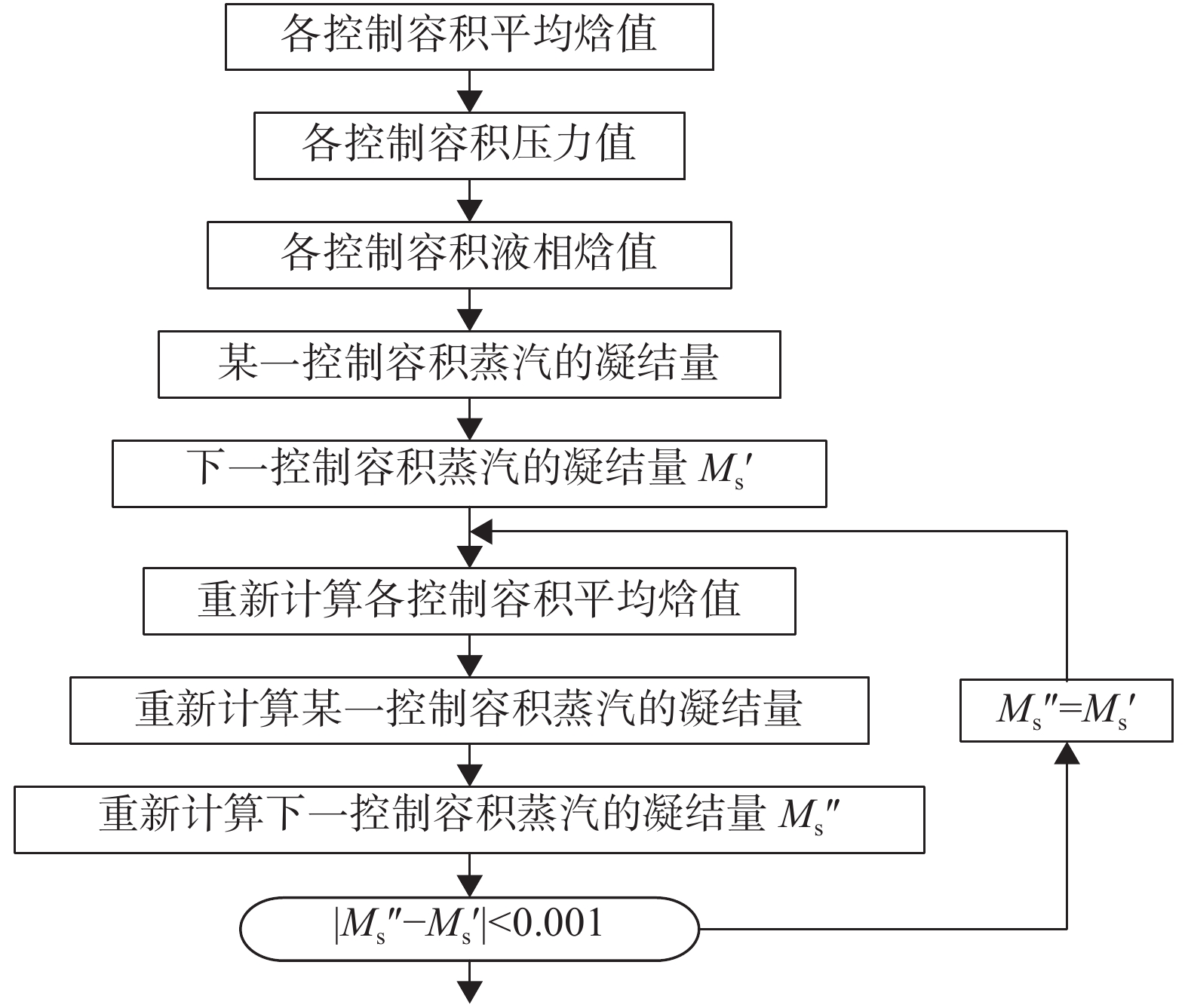
|
| 图 2 计算流程 |
2 计算结果及分析 2.1 实验验证
随着核电机组大型化和调峰需求,凝汽器经常遇到变工况运行问题,主要涉及:循环冷却水进口温度、循环冷却水流量和汽轮机排汽量等参数[13-14]。因此对凝汽器变工况动态特性进行研究十分必要。为了验证模型的准确性,将核电站凝汽器动态实验数据与本文计算结果进行对比。实验数据源于某AP1000核电凝汽器变工况运行数据,在大量变工况运行数据中,选择了两组典型工况,分别为进汽量阶跃增加和进汽量阶跃降低,并采用本文模型对其进行仿真计算。图3给出了100%负荷下凝汽器进汽量阶跃降低和升高后凝汽器压力的变化情况。由图3可知,随着汽轮机排汽量阶跃降低,进入凝汽器工质的总焓降低,在循环水流量不变的前提下,凝汽器内部温度下降,进而导致凝汽器压力降低。进汽量阶跃增加工况的仿真结果与实验值较为吻合,进汽量阶跃降低工况计算值略偏离实验值,二者偏差为2.97%以内。由于本文模型中将冷却管束简化为单根管,没有考虑流经多根单管的凝结水的二次冷却,因此计算值略偏离实验值,但误差仍在允许范围之内。
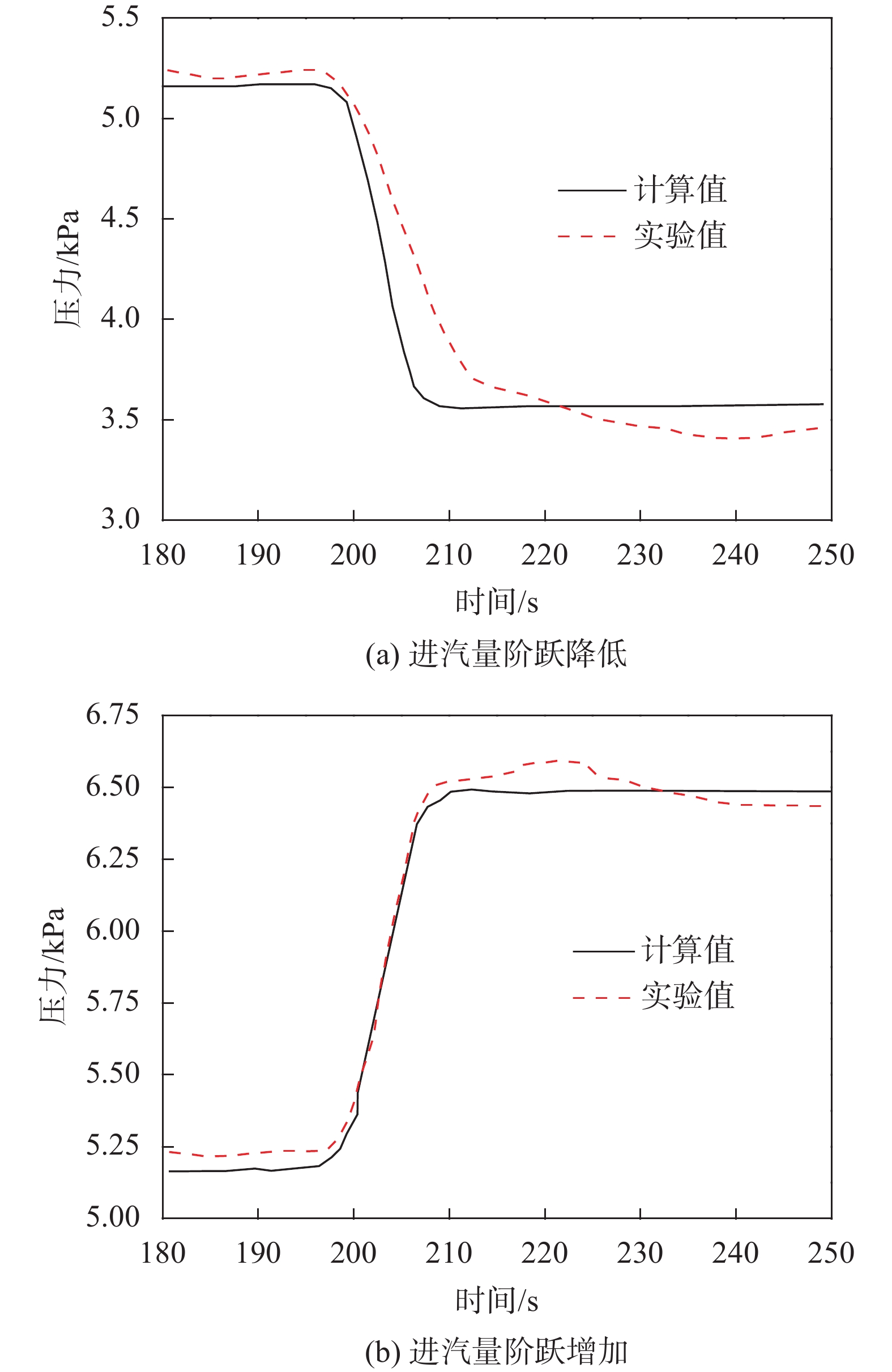
|
| 图 3 计算值与实验值对比 |
2.2 循环冷却水温度的影响
当循环冷却水进口温度发生改变时,凝汽器内的压力和对数传热温差都将发生变化。假设循环冷却水流量不变,初始进口温度为18 ℃,在t=8 000 s处,循环冷却水初始进口温度出现阶跃变化。图4(a)给出了进口温度变为4 ℃、9 ℃、13 ℃、21 ℃、25 ℃和29 ℃后的凝汽器压力随时间的变化情况。图4(b)给出了不同循环冷却水流量下凝汽器压力随冷却水进口温度的变化情况。从图4可以看出,随着循环冷却水进口温度增加,凝汽器壳侧压力也会增加。由于冷却水进口温度上升后,但冷却倍率和给水温升没有变化,因此对数温差下降,凝汽器的换热能力下降,循环水出口温度上升,导致管束金属壁面温度上升,最终凝汽器压力上升。在循环冷却水流量较小的情况下,入口温度对凝汽器运行特性的影响更为显著。夏季气候炎热,海水温度较高,此时低负荷运行工况下凝汽器的压力可达9~13 kPa,高的背压将严重影响汽轮机效率,降低机组出力。因此,在凝汽器实际运行过程中,需严格监测循环冷却水入口温度的变化,防止其对汽轮机背压和凝汽器内各项参数产生较大影响。
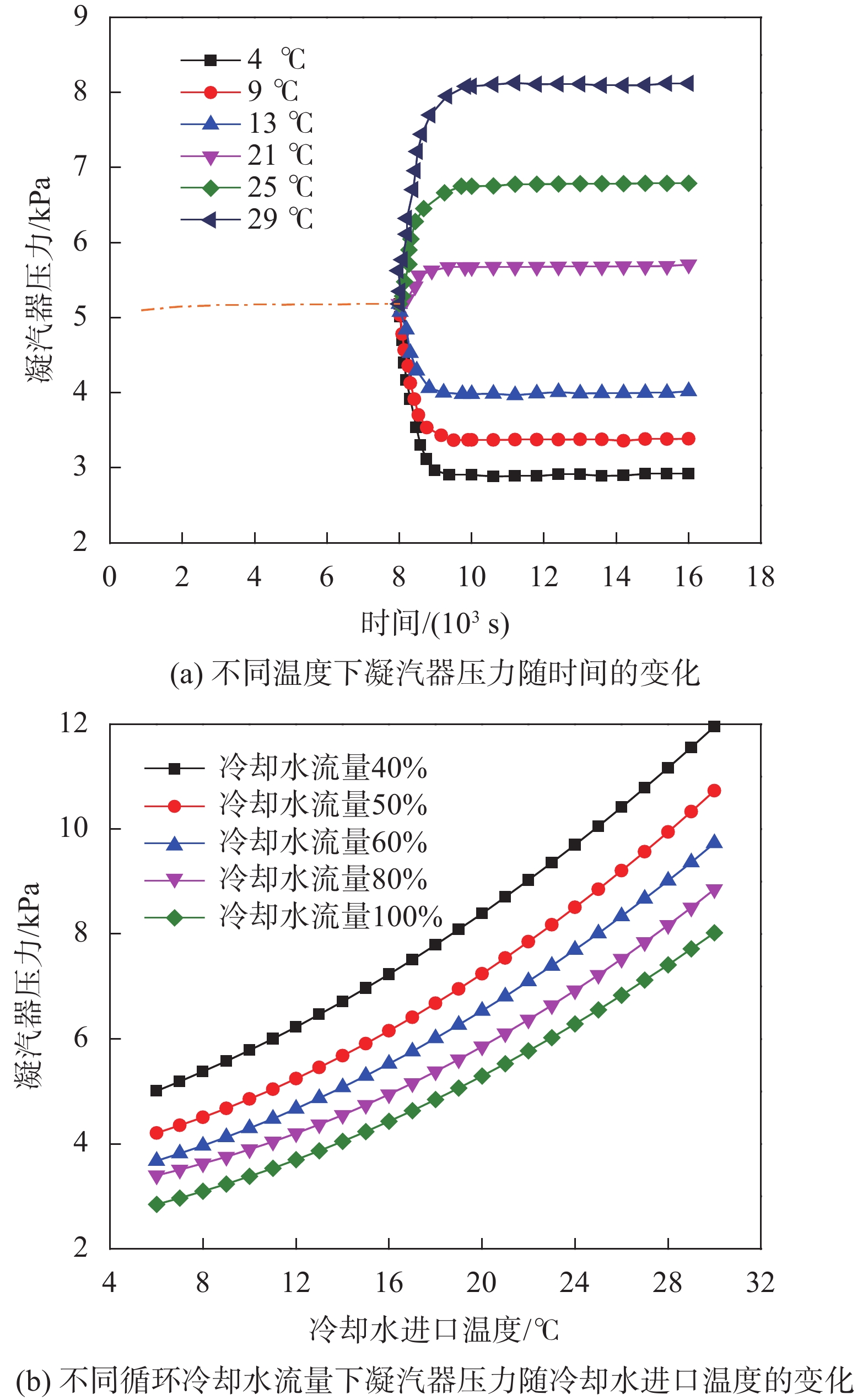
|
| 图 4 循环冷却水温度的影响 |
2.3 循环冷却水流量的影响
除冷却水进口温度外,冷却水流量也会对凝汽器真空产生较大影响。若冷却水进口温度保持18 ℃不变,初始流量为90%设计流量,在t=8 000 s处,循环冷却水初始流量出现阶跃变化。图5(a)给出了循环冷却水流量为40%、50%、60%、80%设计流量下凝汽器压力随时间的变化情况。图5(b)给出了不同进口温度下凝汽器压力随冷却水流量的变化情况。根据热平衡方程,当冷却水流量下降后,凝汽器内部的换热能力将显著下降,此时汽液两相流将不能按照设计参数凝结,凝汽器壳侧压力将增加。从图5(a)看,冷却水流量偏离设计工况越多,凝汽器压力增加的速度越快。为了保证凝汽器最佳真空,应该保证足够多的循环冷却水流量。实际工程中循环冷却水最佳流量需要根据水泵性能、冷却水进口温度、供水方式等多个因素共同确定。
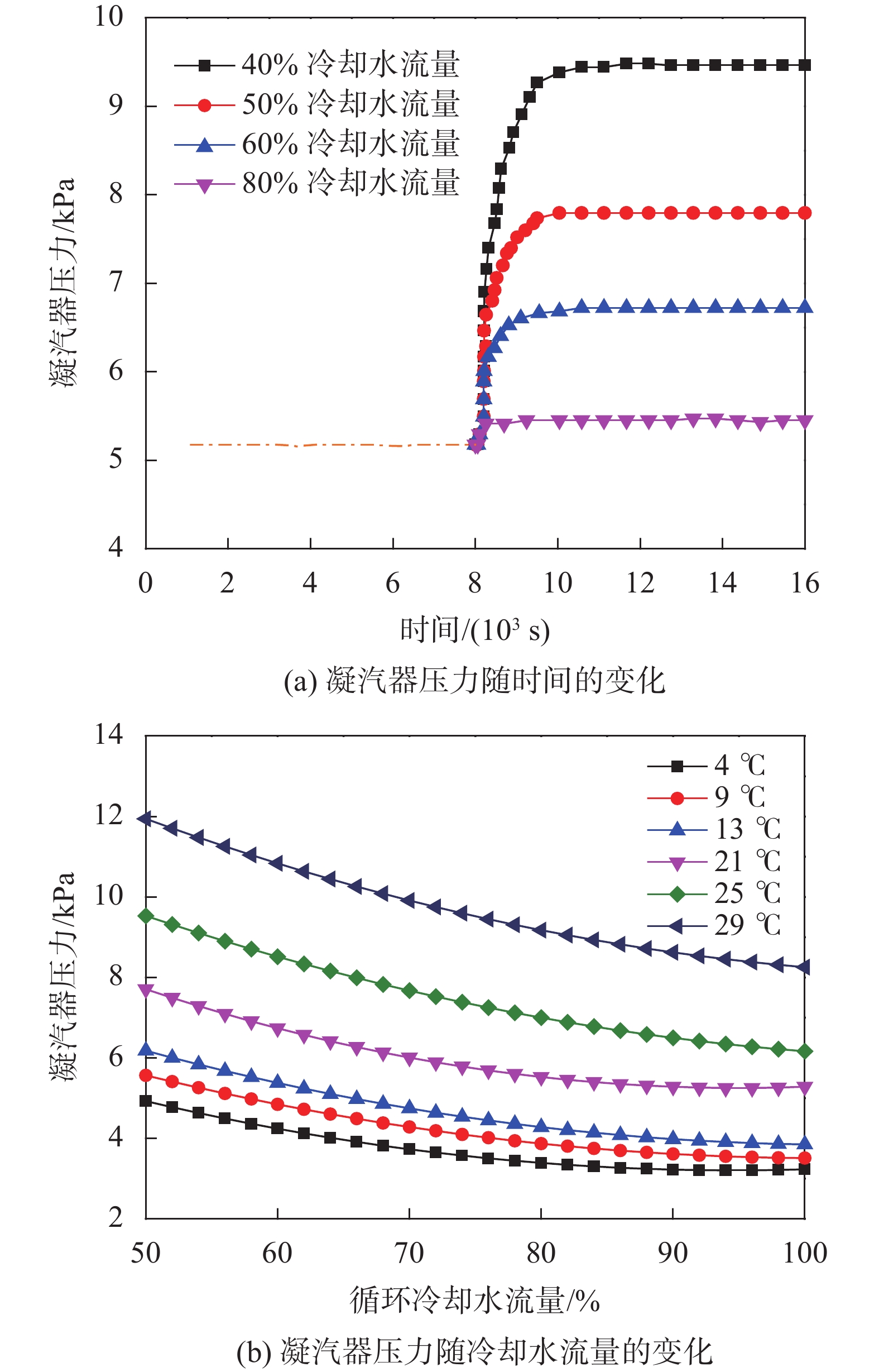
|
| 图 5 循环冷却水流量的影响 |
2.4 汽轮机排汽量的影响
假设循环冷却水流量、温度均不变,冷却水进口温度为18 ℃,假设初始热负荷为70%,在t=8 000 s处,热负荷出现阶跃变化。图6给出了热负荷为40%、50%、60%、80%、90%、100%情况下凝汽器压力随时间的变化情况。仿真结果表明,随着热负荷的不断降低,凝汽器压力随之降低。根据热平衡方程,当凝汽器内部较为稳定时,汽轮机排汽量突增,汽液两相流携带的热量将急剧增加,凝汽器壳侧温度和焓值将显著上升,循环冷却水出口温度上升,管束金属壁面温度上升,最终凝汽器压力上升。
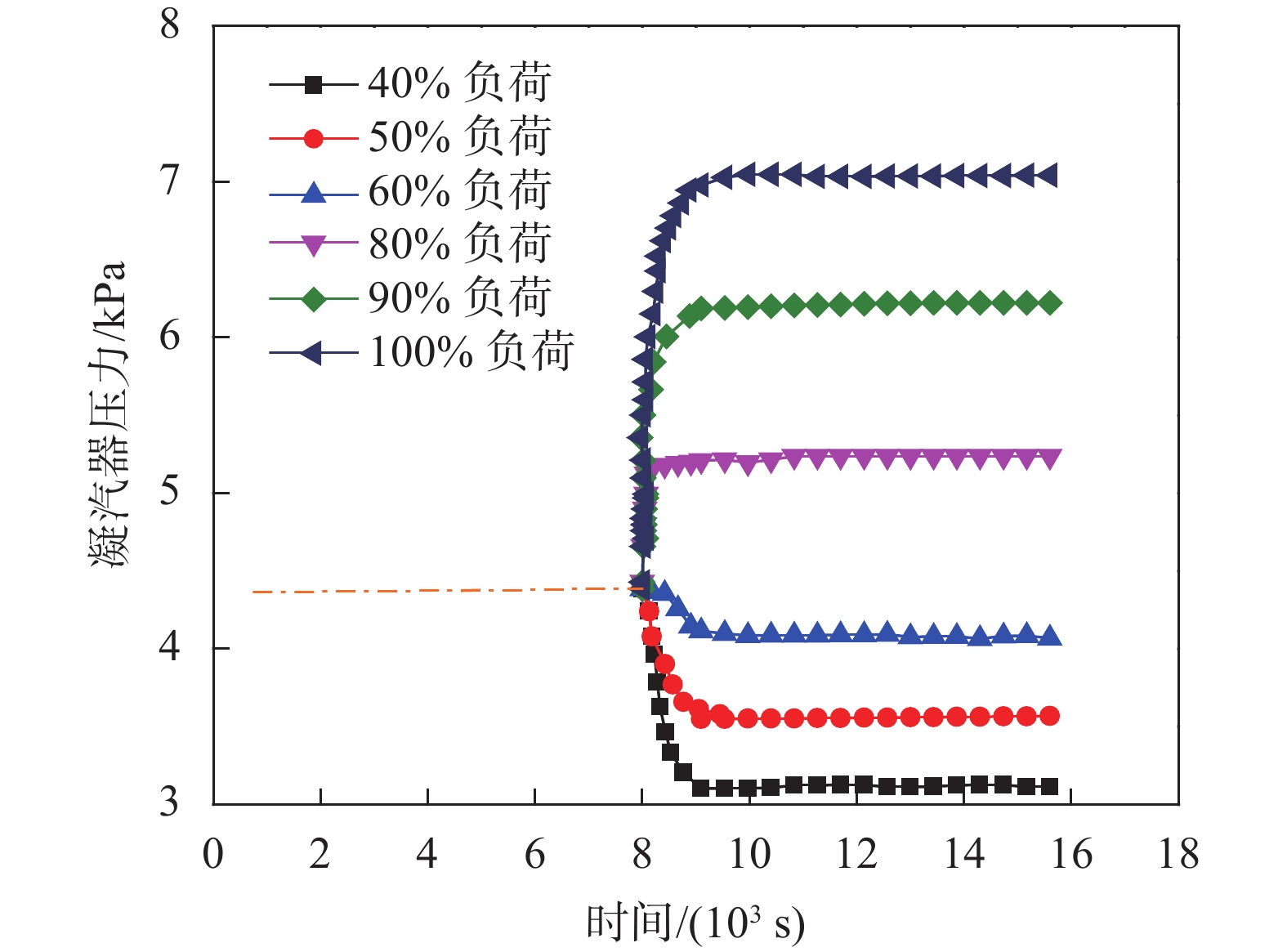
|
| 图 6 汽轮机排汽量的影响 |
仿真结果表明,凝汽器压力随着汽轮机排汽量的增加而上升,随着循环冷却水进口温度的下降而下降,随着冷却水流量的上升而下降。
3 结束语基于分布式热动力学原理,建立核电站表面式凝汽器多压力多节点动态参数模型,采用Adams多步仿真算法对AP1000核电凝汽器在循环冷却水温度、流量、汽轮机排汽量阶跃变化下的动态特性进行分析,仿真结果覆盖了凝汽器的各个运行工况。研究结果表明:凝汽器压力随着汽轮机排汽量的增加而上升,随着循环冷却水进口温度的下降而下降,随着冷却水流量的上升而下降。本文模型能较好地反映凝汽器的动态特性,具有较高的计算精度。可为凝汽器运行优化和故障检修提供理论指导。
| [1] |
PATANKAR G, WEIBEL J, GARIMELLA S. Patterning the condenser-side wick in ultra-thin vapor chamber heat spreaders to improve skin temperature uniformity of mobile devices[J].
International Journal of Heat & Mass Transfer, 2016, 101: 927-936.
|
| [2] |
ORMISTON S, RAITHBY G, CARLUCCI L. Numerical modeling of power station steam condenser part 1: convergence behavior of a finite-volume model[J].
Numerical Heat Transfer Part B Fundamentals, 1995, 27(1): 81-102.
DOI:10.1080/10407799508914948 |
| [3] |
汪国山, 毛新青, 胡国新, 等. 电站凝汽器内流场和传热的准三维数值计算程序PPOC3.0的开发研究[J].
动力工程学报, 2001, 21(5): 1450-1454.
DOI:10.3321/j.issn:1000-6761.2001.05.016 |
| [4] |
侯平利, 陶志伟, 胡友情, 等. 内陆AP1000核电厂常规岛机组冷端优化方法[J].
汽轮机技术, 2010, 52(6): 424-426.
DOI:10.3969/j.issn.1001-5884.2010.06.008 |
| [5] |
侯平利, 江海燕. 核电厂常规岛双背压机组冷端优化计算方法研究[J].
青岛大学学报(工程技术版), 2012, 27(3): 88-91.
DOI:10.3969/j.issn.1006-9798.2012.03.018 |
| [6] |
韩中合, 郑庆宇, 吴智泉, 等. 1000 MW直接空冷凝汽器变工况研究[J].
中国电力, 2012, 45(2): 22-25.
DOI:10.3969/j.issn.1004-9649.2012.02.006 |
| [7] |
HAN X, HAN Z, LI P. Influence of external particles on heterogeneous condensation flow in cascades[J].
Transactions of the Canadian Society for Mechanical Engineering, 2017, 41(2): 265-280.
DOI:10.1139/tcsme-2017-1018 |
| [8] |
付文锋, 刘康, 周兰欣. 耦合末级的1000 MW汽轮机排汽通道数值模拟[J].
中国电机工程学报, 2017, 37(16): 4722-4730.
|
| [9] |
曾申富, 张莉, 屈彬彬. 凝汽器管束布置修正系数随负荷变化的数值计算[J].
汽轮机技术, 2017, 59(3): 169-172.
DOI:10.3969/j.issn.1001-5884.2017.03.003 |
| [10] |
侯方, 李久楷, 谢少雄, 等. 汽轮机转子钢常温与600 ℃超高周疲劳行为研究[J].
中国测试, 2016, 42(2): 9-14.
|
| [11] |
HAN X, HAN Z, ZENG W, et al. Coupled model of heat and mass balance for droplet growth in wet steam non-equilibrium homogeneous condensation flow[J].
Energies, 2017, 10(12): 2033.
DOI:10.3390/en10122033 |
| [12] |
袁小会, 蔡逸飞, 陈国平, 等. 汽轮机低压外缸与凝汽器连接错位分析及改进方案[J].
汽轮机技术, 2017(6): 436-438.
DOI:10.3969/j.issn.1001-5884.2017.06.010 |
| [13] |
韩旭, 韩中合. 汽轮机动叶栅顶部通道湿蒸汽超声速凝结流动特性[J].
化工学报, 2017, 67(9): 3388-3396.
|
| [14] |
付文锋, 张娜, 刘康, 等. 1000 MW机组凝汽器水侧胶球清洗三维数值模拟及结构优化[J].
动力工程学报, 2017, 37(4): 279-284.
|
 2019, Vol. 45
2019, Vol. 45